
Analiza Discriminanta - Principala metoda de credit - scoring
1 Analiza datelor
Analiza datelor constituie o etapa initiala importanta in luarea deciziilor, care permite identificarea cauzelor care duc la aparitia unei situatii decizionale[1]. Astfel, ea reprezinta actiunea de a transforma datele initiale cu scopul de a extrage informatiile utile si de a facilita formularea concluziilor. Procesul de analiza a datelor poate fi definit ca o succesiune de etape ce au ca scop formularea de ipoteze, culegerea informatiilor primare si validarea acestora, construirea modelului matematic care descrie fenomenul analizat precum si formularea concluziilor referitoare la comportamentul acestui model.
Statistica clasica poate prelucra doar un numar restrans de caracteristici ale unui esantion relativ mic de indivizi, utilizeaza estimatii sau teste prea restrictive si emite ipoteze cu un grad mare de aproximare, in timp ce in realitate indivizii sunt descrisi de un numar foarte mare de parametrii, care nu corespund legilor de probabilitate cunoscute apriori.
Astfel intervine analiza datelor, care realizeaza o cercetare globala a relatiei individ - caracteristica, bazandu-se pe reprezentari grafice, mult mai simplu de interpretat decat tabelele voluminoase din statistica clasica. Analiza grafica este completata bineinteles de metodele analizei multidimensionale . Deoarece analiza datelor opereaza cu masive de date complexe, se face apel la metode matematice specifice, la sisteme de programe informatice care permit codificarea datelor si efectuarea sintezelor numerice si grafice. Aceasta inseamna ca, pentru aplicarea metodei de analiza datelor sunt necesare atat cunostinte de statistica, matematica, informatica cat si cunostinte din domeniul investigat.
Aceasta abordare multidimensionala , datorita suportului informatic de care beneficiaza, cunoaste o multitudine de utilizari practice in analiza unor fenomene medicale, fizice, sociologice.
Pe de alta parte, spre deosebire de data mining, analiza datelor are un camp de aplicare mai ingust, avand ca scop verificarea existentei unui anumit model sau extragerea parametrilor necesari pentru adaptarea modelului teoretic la realitate si nu descoperirea de modele ascunse, precum cealalta tehnica mentionata.
Analiza datelor presupune un numar mare de proceduri si metode. Sub cea mai generala forma a sa, o problema de analiza a datelor poate fi formulata ca o problema de testare a uneia sau mai multor ipoteze nule. Informatiile cantitative folosite intr-o analiza, valorile variabilelor retinute dintr-un studiu pe un esantion reprezentativ sunt utilizate cu scopul de a verifica semnificatia statistica a ipotezei nule.
In acelasi timp se pot cauta asemanari si deosebiri intre indivizi conform anumitor criterii, se pot efectua clasificari si ordonari de multimi, se pot analiza relatiile care exista intre caracteristici etc. . In cazul in care caracteristicile sunt corelate atunci se poate reduce dimensiunea analizei doar la caracteristicile independente. Pentru aceasta se va efectua o transformare geometrica a spatiului caracteristicilor, astfel incat sa se poata vizualiza sugestiv, in plan, relatiile dintre indivizi si legaturile dintre caracteristici fara a se pierde un volum semnificativ de informatii.
Ceea ce este important e ca metodele de analiza datelor nu au un caracter abstract. Astfel, aceeasi procedura poate fi utilizata pentru o varietate de situatii, de la jocuri de baseball la cumparaturi in mall-uri sau domeniul educational.
Pentru a identifica locul analizei datelor intr-un studiu statistic, trebuie mai intai prezentate cele trei faze distincte ale acestuia: faza metodologica, cea tehnica si cea de publicare. Faza metodologica presupune stabilirea instrumentelor: unitati si nomenclatoare; cea tehnica reprezinta punerea in practica a instrumentelor. Astfel se stabilesc liste de unitati selectate, se construieste chestionarul, acesta se aplica, raspunsurile sunt verificate manual si automat obtinand in final rezultatele brute. Faza de publicare cuprinde toate metodele si tehnicile de exploatare a bazei de date. In aceasta etapa se obtin o multime de tabele, grafice dintre care se pastreaza cele relevante, se interpreteaza, se explica , toate acestea cu ajutorul tehnicilor de analiza datelor. Prin urmare se constata ca aceasta ocupa un loc din ce in ce mai important in modelarea rezultatelor brute si transformarea lor pentru a facilita intelegerea rezultatelor studiului de catre cititorul neavizat .
Analiza datelor cuprinde doua mari grupe de metode: metodele analizei factoriale si metodele de clasificare automata. Analiza factoriala se bazeaza pe nori de puncte si presupune identificarea axelor factoriale. Metodele analizei multidimensionale au ca scop reducerea numarului de variabile prin construirea de caracteristici sintetice care combina pe cele initiale. Principalele metode utilizate de aceasta sunt:
¤ Analiza componentelor principale
¤ Analiza corespondentelor
¤ Analiza canonica
¤ Analiza discriminanta factoriala
¤ Analiza corelatiei
¤ Analiza variantei
¤ Analiza regresiei liniare si neliniare
Clasificarea automata presupune gruparea indivizilor in clase omogene in functie de un anumit criteriu iar rezultatele se prezinta de cele mai multe ori sub forma unui arbore. Aceste tehnici se bazeaza pe algoritmi (ascendenti sau descendenti) si nu pe calcule formale.
In concluzie, exista o mare varietate de metode si tehnici de analiza a datelor, generata de importanta utilizarii analizei datelor in cele mai diferite domenii ale stiintei. Dintre aceste, analiza datelor este cel mai frecvent utilizata si cu rezultate de o mare utilitate in domeniul economico-financiar si domeniul social.
2 Analiza discriminanta - generalitati
Analiza discriminanta este o metoda ce face parte din grupa metodelor explicative de analiza a datelor. Ea utilizeaza o variabila de explicat (Y) si mai multe variabile explicative (X1 ,X 2,, Xp) cantitative sau binare. Aceasta se aplica unei populatii de indivizi caracterizate prin variabile continue sau categoriale si ale carei componente sunt apriori (uneori natural) impartite in grupuri. Scopul analizei discriminante este acela de a clasifica una sau mai multe observatii noi in aceste grupuri deja precizate.
Sintetizand, putem sa afirmam ca in analiza discriminarii populatia de indivizi care au fost cercetati este impartita in grupuri si ca dispunem de datele observate pentru fiecare dintre acesti indivizi. In ceea ce priveste grupurile, in unele situatii acestea apar in mod natural, in altele ele sunt rezultatul unei analize anterioare.
Scopul unei metode de discriminare variaza dupa domeniul in care se aplica. Sa exemplificam cu urmatoarele doua situatii. [4]
Exemplul 1. Presupunem ca ne aflam in domeniul postal si avem in vedere punerea la punct a unui sistem de recunoastere si de triere automata a unor coduri postale scrise manual. In acest caz, populatia analizata este constituita din secvente de 6 cifre (scrise manual) - 10 grupuri posibile pentru fiecare cifra a secventei - avand fiecare caracteristicile sale morfologice. Scopul unei analize de separare (discriminare) in acest context este pur decizional, fiind vorba de a elabora reguli de decizie pentru recunoasterea celor 10 cifre cu minim de eroare.
Exemplul 2[5]. In septembrie 1992 francezii s-au pronuntat prin referendum asupra ratificarii tratatului de la Maastricht privind actul de infiintare a Uniunii Europene. Votul a impartit votantii in doua grupuri: unii au fost pentru, altii impotriva tratatului. Comentatorii politici au fost interesati, la vremea respectiva, sa descrie din punct de vedere social si economic portretul partizanilor, dar si pe cel al opozantilor tratatului. In acest exemplu suntem confruntati cu o problema discriminanta dar, de aceasta data, scopul ei nu este decizional, ci explicativ: se urmareste sa se descopere cat mai bine care au fost motivatiile electorilor in decizia de vot.
Distingem doua demersuri succesive, de ordin descriptiv si apoi decizional[6]:
- Se identifica functii liniare discriminante pe baza esantionului de volum n , care sunt combinatii liniare de variabile explicative (x1,x2,.,xp) astfel incat aceste valori sa separe cel mai bine cele q clase intre ele .
- Se identifica clasa de apartenenta pentru n' noi indivizi descrisi cu ajutorul celor p variabile. Aceasta este de fapt o problema de clasificare in clase preexistente in opozitie cu problemele de clasificare clasice, care presupun realizarea de clase cat mai omogene dintr-un esantion.
In concluzie, putem afirma ca, in general, analiza discriminanta are trei scopuri bine precizate, si anume:[7]
- Sa construiasca un spatiu discriminant. In cazul analizei discriminante simpla (Y are doua stari) se determina o axa discriminanta Z care explica apartenenta unei unitati la o clasa sau alta. In cazul analizei discriminante multipla se determina mai multe combinatii liniare independente (axe discriminante) de variabile explicative si trebuie analizat spatiul determinat de acele axe care separa cel mai bine unitatile studiate, in clasele determinate de starile variabilei Y.
- Un scop decizional, destul de frecvent, ce are in vedere construirea unei reguli de repartizare a indivizilor la un grup, regula ce poate fi aplicata si in viitor. Respectiv, cunoscand nivelul variabilelor explicative si utilizand functiile discriminate vor fi repartizate noile unitati in clasele deja formate. Aceasta se poate realiza prin doua procedee: unul determinist, care repartizeaza unitatea la clasa pentru care distanta pana la centroid este cea mai mica si unul probabilist unde se calculeaza probabilitatile de apartenenta la diferite clase, iar unitatea se aloca clasei pentru care se inregisteaza probabilitatea cea mai mare. O regula buna de afectare este aceea care va conduce la erori de clasare a observatiilor viitoare cat mai mici posibile.
- Un scop explicativ, prin care se urmareste sa se descopere variabilele explicative care contribuie cel mai mult la diferentierea claselor definite de variabila de explicat (apriori), astfel se identifica ponderea influentei variabilelor explicative in variatia variabilei de explicat, construind mai multe combinatii liniare si alegand-o pe cea mai buna.
1 Analiza discriminarii decizionale - reguli de alocare
Sa presupunem ca avem o populatie Π de indivizi impartita in J grupuri (subpopulatii) disjuncte Π1, Π.., Πj- prin valorile 1,2.j ale unei variabile categoriale. Fiecare individ al populatiei este descris prin p variabile continue, notandu-se valorile care il caracterizeaza cu x=(x1.xp) si deci poate fi identificat cu un punct din Rp
O regula de discriminare produce o separare a spatiului Rp in multimile R1,R2.Rj astfel incat daca x∈Rj atunci individul caracterizat de x va fi considerat ca apartinand grupului (subpopulatiei) Πj . Scopul principal in construirea unei reguli de discriminare este acela de a gasi regiuni "bune" Rj astfel incat eroarea de clasificare gresita a unui individ sa fie cat mai mica. Vom prezenta in continuare cateva reguli de discriminare, pentru cazul in care sunt cunoscute repartitiile populatiilor.
A) Regula de discriminare Bayes
Notam cu fi(x) densitatea de probabilitate a populatiei Πi,i
Prin regula de alocare bayesiana, x se aloca acelui grup (populatii) Πj corespunzator probabilitatii a posteriori maxime, (sau grupului pentru care costul mediu este minim), adica:
 (5)
(5)
fi(Πi/x) fiind probabilitatea a posteriori asociata populatiei Πi
Prin formula lui Bayes avem:
 (6)
(6)
Expresia de la numitor [10]  reprezinta probabilitatea pentru o
observatie, ca valorile caracteristicii sale observate in Rp
sa fie x= (x1, x2,.,xp).
reprezinta probabilitatea pentru o
observatie, ca valorile caracteristicii sale observate in Rp
sa fie x= (x1, x2,.,xp).
Astfel putem folosi regula de alocare:
![]() (7)
(7)
Prin urmare, regiunea corespunzatoare regulii de alocare (7) se poate descrie astfel:
![]() (8)
(8)
B) Regula de discriminare prin verosimilitate maxima
Regula de discriminare prin verosimilitate maxima (ML = maximum likelihood ) aloca un individ descris prin punctul x la acea populatie Πj pentru care se realizeaza probabilitatea maxima, adica: X este alocat lui Πj
![]() (9)
(9)
In regula de discriminare prin verosimilitate maxima consideram πi probabilitatea a priori asociata populatiei Π (pentru i ), evident cu proprietatea
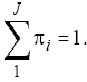
Sa notam cu Lj(x) acea densitate de probabilitate Fj(x) care realizeaza maximul (9). Matematic, multimea Rj este definita astfel :
![]()
Sa evaluam eroarea de clasificare gresita. Sa presupunem ca avem doua clase, adica J = Putem calcula probabilitatea de a aloca pe x la grupul 2 atunci cand el este de fapt in grupul 1 astfel:
![]() (10)
(10)
si similar, probabilitatea de a aloca pe x la grupul 1 atunci cand el este de fapt in grupul 2 este
![]() (11)
(11)
Putem sa construim o regula de alocare asociind costurile unei clasificari eronate. Astfel, o clasificare gresita determina un cost al erorii de clasificare a unui individ din populatia Πi in regiunea Rj. Fie πi probabilitatea a priori asociata populatiei Πi, adica probabilitatea ca un individ oarecare, ales aleatoriu, sa fie din populatia Πi. Aceasta probabilitate a priori poate fi estimata pe baza experientei anterioare asupra populatiei studiate.
Folosind notiunile precizate mai sus, putem sa calculam un cost mediu CM al erorii de clasificare prin:
![]() (12)
(12)
Evident, vom incerca sa construim reguli de alocare pentru care expresia (12) sa aiba valoare minima. Pentru gruparea in doua populatii regula de discriminare bazata pe realizarea unui cost mediu minim este data de urmatoarea teorema. Formula lui CM conduce la construirea urmatoarelor regiuni de alocare:

Observatie. Regula de alocare prin verosimilitate maxima este un caz particular al regulii de alocare pe baza costului mediu minim. Ea se obtine luand costurile erorilor egale intre ele, C(2|1)=C(1|2)=1, si de asemenea probabilitatile a priori egale, π
Daca consideram ca cele doua
populatii sunt repartizate normal, ![]() , cunoscand ca densitatile de
probabilitate sunt:
, cunoscand ca densitatile de
probabilitate sunt:
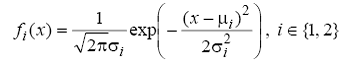
Astfel, x va fi alocat la Π - prin regula verosimilitatii maxime - daca x∈R1= . In acest caz, conditia f1(x)>f2(x) este echivalenta cu
 (13)
(13)
Sa presupunem ca μ , σ1=1 si μ Aplicarea formulei (13) ne conduce la definirea regiunilor de alocare astfel:
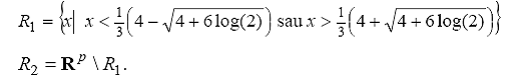
In cazul in care densitatile de repartitie au aceleasi dispersii si sa presupunem ca μ1< , regula de verosimilitate maxima conduce la definirea urmatoarelor regiuni:
![]()
Sa presupunem acum ca avem un numar oarecare de subpopulatii, fie ele J si ca densitatile de probabilitate pe spatiul Rp sunt normale cu media μ = ( J )si matricea de varianta-covarianta Σ. Avem urmatoarea Teorema. Prin regula de verosimilitate maxima (ML) un punct x se aloca la populatia Πj daca si numai daca
![]()
adica punctul se aloca acelei populatii pentru care distanta Mahalanobis intre punct si valoarea medie este cea mai mica.
Observatie. In practica, vectorul mediilor este estimat prin centrele de greutate ale grupurilor respective, iar matricea de varianta-covarianta este estimata prin matricea inertiei intre grupuri.
Observatie: Regula Bayes este identica cu regula de discriminare ML daca probabilitatile a priori sunt πi=1/j.
2 Analiza discriminarii factoriale
Tehnica discriminarii factoriale este asemanatoare cu tehnica componentelor principale .
Daca avem de rezolvat o problema de discriminare, atunci avem indicata si o variabila raspuns de tip categorial. Sa presupunem ca aceasta are k modalitati; prin urmare, esantionul de n indivizi va fi grupat, dupa variabila categoriala in k clase.
Matricea X(n p) a datelor reprezinta n indivizi asupra carora s-au masurat p variabile, aici variabile explicative. Aceasta matrice o putem privi fie linie cu linie exprimand informatii despre cei n indivizi, fie coloana cu coloana exprimand informatii despre cele p variabile. Prin urmare:
- oricarui individ i ii corespunde in matricea X o linie, adica un vector cu p elemente, care va fi scris: ; xi=(xi1,xi2,.xip) Rp.
- oricarei variabile j ii corespunde in matricea X o coloana cu n elemente, care va fi notata: ; xj=(x1j,x2j,.xnj)T Rn
Notam cu m= (m1,m2,.mp) vectorul mediilor celor p variabile, iar punctul de coordonate (m1,m2,.mp) din Rp este numit centrul de greutate al norului de puncte;
Notam cu s=(s1,s2,.sp) vectorul abaterilor standard calculate pentru vectorii coloana ai matricei X.
Mai consideram :
- matricea V= (sij) i=1,2,.n ; j=1,2,.p de varianta-covarianta estimata pentru cele p variabile explicative;
- vectorul mediilor variabilelor explicative pentru fiecare dintre cele q clase. Corespunzator clasei l, fie ml=(m1ll,m2l,.mpl) vectorul mediilor celor p variabile explicative calculat pe baza indivizilor din clasa l; el se numeste centrul de greutate al clasei l; evident l=1,2,.q
- matricea de covarianta Wl a celor p variabile explicative, matrice calculata pentru indivizii clasei l, l=1,2,.q;
- matricea W=W1+W2+.+Wp, care este numita matricea de covarianta pentru interiorul claselor;
- matricea B=V-W, care este numita matricea de covarianta intre clase.
Fie in spatiul Rp o dreapta Δ de versor u=(u1,u2,up)T . Daca in analiza componentelor principale alegeam acea dreapta care sa recupereze cea mai mare cantitate de informatie din informatia totala a norului de puncte, in analiza discriminarii vom alege acea dreapta care permite o separare "optima" a proiectiilor in clase. Pentru a vedea la ce ne conduce acest obiectiv, consideram un individ j ale carui coordonate in spatiul variabilelor sunt (xj1,xj2,.xjp) si care se identifica cu un punct in Rp. Proiectand acest punct pe dreapta Δ obtinem valoarea
![]() (18)
(18)
care reprezinta distanta
proiectiei punctului pe dreapta Δ fata de centrul de
greutate al norului de puncte m.
Valoarea cj asociata individului j se mai numeste scor asociat dreptei Δ. Pentru
ansamblul indivizilor putem scrie vectorul coloana al scorurilor![]() (19)
(19)
Vectorul u=(u1,u1,.up)T, versor al dreptei Δ, se numeste factor de discriminare iar C se mai numeste componenta de discriminare.
Un model liniar al problemei de discriminare poate fi urmatorul:
![]() (20)
(20)
in care z este o noua variabila, exprimata printr-o functie liniara de cele p variabile explicative. Daca α1=u1, α2=u2, αp=up , expresia din (20) este numita functie de discriminare iar coeficientii sai se mai numesc si coeficienti de discriminare.
Tehnica discriminarii factoriale se bazeaza pe descompunerea variantei totale V in cele doua componente ale sale si anume W varianta pentru interiorul claselor si B pentru varianta intre clase, avem V = W + B .
Analog tehnicii componentelor principale, inlocuind indivizii prin proiectiilor lor pe o axa de versor u=(u1,u1,.up)T , avem:
![]() (21)
(21)
Scopul unei tehnici de discriminare este acela de a gasi acea axa Δ pentru care discriminarea proiectiilor pe ea sa fie maxima. Un caz ideal ar fi acela in care covarianta pentru interiorul claselor este nula uTWu=0, corespunzand situatiei in care toate punctele dintr-un grup sunt proiectate in centrul de greutate al grupului respectiv. Am avea in acest caz uTVu= uTBu iar alegerea celei mai bune axe de discriminare revine la maximizarea expresiei uTBu.
In practica se maximizeaza insa raportul
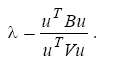 (22)
(22)
Se observa ca acesta ia valori in intervalul [0,1] si exprima, in procente, bonitatea discriminarii.
Aflarea versorului u solutie a problemei (22) se reduce la aflarea solutiei sistemului algebric de ecuatii:
![]() (23)
(23)
cu alte cuvinte, u va trebui sa fie unul dintre vectorii proprii ai matricei V-1B, corespunzator valorii proprii maxime. Daca notam cu gh (x) un asemenea vector propriu, el ne va determina primul factor de discriminare. Apare o prima componenta de discriminare C1=X gh (x). Luand in continuare urmatoarea valoare proprie obtinem al doilea factor de discriminare gh (x) si, corespunzator lui, a doua componenta de discriminare , etc. C2=X gh (x).
Sa consideram ca variabila categoriala ce imparte populatia in clase are doar doua modalitati, deci q = Se poate demonstra ca vectorii proprii diferiti de 0 ai matricei
V-1Bsunt in numar de q - 1. Avem asadar doar o singura functie de discriminare si un singur factor de discriminare
![]()
Clasificarea indivizilor pe baza functiei de discriminare gasite se face folosind relatia (18) pentru proiectarea centrelor de greutate ale celor doua clase pe axa de discriminare. Fie aceste proiectii c1,c2 . Scorul de separare (cutting score) al indivizilor pe axa de discriminare se obtine cu formula:
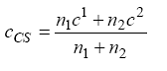 (in care am notat cu n1,n2 frecventele
celor doua clase).
(in care am notat cu n1,n2 frecventele
celor doua clase).
Regula de decizie in reclasificare, pentru un individ cu scorul cj , este urmatoarea
- daca cj<cCS , atunci individul jeste repartizat primei clase, dimpotriva
- daca cj>=cCS, atunci individul j este repartizat celei de-a doua clase.
Rata succesului discriminarii se calculeaza cu formula:
 (25)
(25)
in care am folosit notatiile din urmatorul tabel:
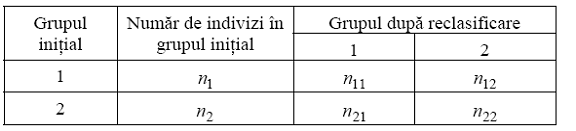
Pentru doua clase cu frecvente egale, o procedura aleatoare de repartizare in clase ar avea o rata a succesului de 50%; asadar, diferenta dintre Ps si 50% poate fi folosita ca indicator al calitatii discriminarii.
Daca numarul de variabile este prea mare, atunci utilizarea analizei discriminante este foarte costisitoare. De aceea este foarte utila limitarea numarului de variabile[12]. Acest lucru se poate realiza in 2 moduri : fie mai intai se utilizeaza analiza componentelor principale fie se utilizeaza analiza discriminanta prin metoda "pas cu pas".
Astfel, daca 2 variabile sunt puternic corelate, vom lua in considerare doar una dintre ele .
3 Aplicarea analizei discriminante in cazul variabilelor calitative
In cazul in care variabilele explicative sunt calitative si nu cantitative asa cum s-a presupus pana acum, calculul functiilor liniare nu se mai poate realiza (matricea x este singulara) dar se pot utiliza axele principale.
Mai intai se aplica analiza componentelor principale asupra bazei de date cu variabilele codificate (fara a fi luata in considerare variabila y, dependenta). Aceasta metoda ne permite restrangerea variabilelor calitative intr-un numar mic de variabile cantitative .In continuare se poate aplica analiza discriminanta asupra acestora din urma, ca si variabile explicative si y ca si variabila e explicat.
Puterea discriminanta a unei variabile calitative cu doua sau mai multe stari se determina cu ajutorul tabelului de contingenta intre cele m stari ale variabilei si cele p grupe discriminante.
|
Stari ale variabilei |
Total |
|||||||
|
Grupe |
|
j |
m | |||||
|
i p |
nij |
ni. |
||||||
|
Total |
n.j |
n |
||||||
Cu ajutorul testului Hi patrat puterea discriminanta a variabilei calitative, adica dependenta dintre apartenenta la o grupa si starile variabilei este acceptata sau refuzata in functie de valoarea statisticii urmatoare[15]:

In ipoteza in care intre cele m stari
si p grupe nu exista legatura, aceasta statistica
urmeaza o lege ![]() 2 ((p-1)(m-1)).
2 ((p-1)(m-1)).
Pentru a putea aplica acest test, trebuie ca numarul de observatii pentru fiecare combinatie nij sa fie mai mare sau egal cu 5. Acest tabel poate sugera regrupari ale starilor variabilelor sau poate identifica asociatii de grupuri intre care diferentele nu sunt majore.
Metoda Disqual[16] - perfectionata de J.M. Bouroche si G.Saporta (1990) - a fost utilizata in special de institutiile de credit. Principala conditie de aplicare a acestei metode o reprezinta necesitatea ca toate variabilele sa fie calitative. Pentru a utiliza aceasta metoda trebuie in prealabil pregatite variabilele: este esentiala o definire eficace a repartizarii variabilelor in clase, urmata de codificarea corespunzatoare a acestora.
Ea prezinta avantajul de a tine cont de evolutia non-liniara a unor variabile in raport cu fenomenul studiat, la fel ca si metoda regresiei logistice si a arborilor de decizie. Un alt avantaj il reprezinta faptul ca nu se bazeaza pe ipoteze cu privire la legea de probabilitate urmata de variabile.
4 Utilizari
Analiza discriminanta se utilizeaza in domeniul bancar - credit scoring, unde in functie de caracteristicile solicitantului, acestuia i se acorda sau nu imprumutul, in raport cu valoarea unui scor ce permite sa se estimeze riscul de nerambursare.
Un alt domeniu de aplicare al analizei discriminante este cel al comportamentului consumatorului, unde se poate prevedea probabilistic comportamentul uni individ fata de un anumit produs sau serviciu, in functie de starea inregistrata de variabilele explicative ce definesc o anumita atitudine.
Aceasta metoda poate fi utilizata si pentru alte cercetari economice (analiza riscului de faliment, analiza utilizarii terenurilor agricole ), dar si in alte domenii precum fizica, inginerie, medicina, biologie, genetica, ecologie, etc. .
5 Evaluarea performantelor
Masurarea calitatii rezultatelor unei analize discriminante se poate realiza fie plecand de la procentul celor corect repartizati (sau incorect clasati) in fiecare clasa fie pe baza procentului global al celor corect clasati. Pentru inceput se poate calcula procentul celor clasati corect din esantionul de invatare, ceea ce va oferi o idee optimista despre calitatea discriminarii . Acest procent creste o data cu numarul parametrilor modelului si poate atinge un nivel foarte bun, daca numarul parametrilor este considerabil , fara ca aceasta sa insemne ca modelul permite realizarea unei previziuni corecte. Metoda esantionarii recomanda aplicarea analizei discriminante doar pe o parte a esantionului de invatare (80% ) si testarea regulilor de discriminare pe cei 20% neutilizati anterior.
Performantele se pot exprima in acelasi timp in probabilitati de apartenenta aposteriori la fiecare din grupele de discriminare. Performanta nu trebuie sa fie legata doar de esantionul de invatare pe baza caruia s-au construit functiile de discriminare , ea trebuie sa permita o aplicare generala a metodei. Aceasta problema de validare este cruciala pentru a permite o utilizare sistematica. Se pot utiliza mai multe tehnici : esantioane test, validarea incrucisata , "bootstrap".
In cazul in care variabila dependenta este binara un instrument foarte utilizat este curba ROC (Receiver Operating Characteristics curve)[18]. Pe baza matricei confuziilor
|
Grupare dupa regula |
Grupare initiala 2 |
Total |
|
|
|
|
|
Total |
|
|
se determina urmatoarele rapoarte :
![]() proportia
predictiilor corecte pentru observatiile pentru care y=1
proportia
predictiilor corecte pentru observatiile pentru care y=1
![]() proportia
predictiilor corecte pentru observatiile pentru care y=2
proportia
predictiilor corecte pentru observatiile pentru care y=2
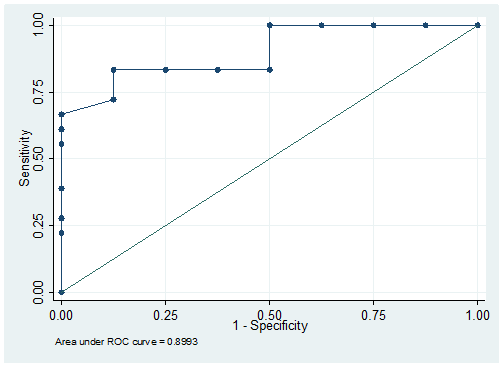
Pentru valori diferite ale scorului z se obtin valori diferite pentru cele doua rapoarte si astfel putem trasa curba ROC. In cazul unui model ideal, curba porneste din coltul stanga-jos si ajunge in dreapta-sus trecand prin punctul de coordonate (0,1), ceea ce inseamna 100% predictii corecte. Masura utilizata pentru aprecierea puterii predictive a modelului este aria aflata sub curba ROC. Cu cat aceasta este mai mare, cu atat modelul este mai bun.
In mod ideal am dori ca procentul celor bine clasati sa fie 100% , dar in realitate daca proportia acestora depaseste 75% este bine. Proportia reala a clasamentelor corecte este probabilitatea ca regula de decizie sa repartizeze corect indivizii dintr-un nou esantion extras din aceeasi populatie totala. In acelasi timp, proportia celor clasati incorect este probabilitatea ca regula de decizie sa repartizeze incorect indivizii din noul esantion extras din populatia totala.
Metodele de validare sunt utilizate pentru a stabili in ce masura am atins probabilitatile teoretice de clasificare corecta, pentru a cunoaste mai bine puterea reala de discriminare a fiecarei functii construite.
3 Etapele analizei discriminante in SPSS
Problema de rezolvat poate fi formulata astfel: fiind data o variabila de explicat (Y) avand k stari si p variabile explicative (X1 ,X 2,, Xp) , trebuie gasita una sau mai multe combinatii liniare de variabile explicative de forma:
![]()
diferentiind cel mai bine cele k grupe formate prin raportarea la starile variabilei de explicat (Y).
Prima combinatie liniara este aceea in care varianta dintre clase este maxima iar varianta din interiorul claselor minima . Apoi o alta combinatie liniara, necorelata cu prima, care imparte cel mai bine clasele. Aceste combinatii liniare sunt numite functii liniare discriminante.[20]
Procedeul de rezolvare este fundamentat pe faptul ca matricea de varianta - covarianta totala T , poate fi descompusa in doua parti:
Matricea de varianta - covarianta intre grupe (B)
Matricea de varianta - covarianta din interiorul grupelor (W), determinata ca o suma de k matrici , fiecare matrice fiind cea de varianta - covarianta din cadrul grupei.
T=B+W
Fie u un vector nenul u RN . Atunci u'Tu=uBu+u'Wu
Problema analizei discriminante poate fi formulata: sa se gaseasca o directie u pe RK astfel incat u'Bu sa fie maxim.
Acestui vector ii putem asocia o functie liniara ![]() care sa fie
data de proiectia lui Xh pe u.
care sa fie
data de proiectia lui Xh pe u.
Mai intai trebuie studiata puterea de discriminare a fiecarei variabile , utilizand analiza variantei. Avand ecuatia de descompunere a variantei totale pentru o variabila Xi , respectiv:
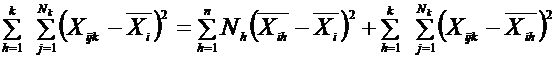
Pentru masurarea puterii de discriminare a variabilei Xi, se utilizeaza raportul de determinatie.

Cu cat acest raport tinde la 1, cu atat puterea de discriminare a variabilei Xi este mai mare. Variabila Fisher F , unde
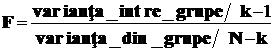
pentru
un nivel de semnificatie ![]() permite sa se
precizeze care sunt variabilele semnificativ discriminante.
permite sa se
precizeze care sunt variabilele semnificativ discriminante.
In ceea ce priveste variabilele explicative, acestea nu trebuie sa fie corelate intre ele sau sa fie putin corelate. Daca variabilele explicative initiale sunt corelate intre ele se recomanda aplicarea prealabila a analizei componentelor principale si utilizarea noilor variabile ca variabile explicative.
Problema analizei discriminante consta in a cauta o directie sau mai multe in care varianta totala T se descompune in cele doua componente , minimizand pe W si maximizand pe B.
Numarul axelor discriminate (Z) este egal cu min(p;k-1). De asemenea axele discriminate (Z) sunt vectori proprii ai matricii (T-1B), iar prima axa (Z1)este asociata acelei valori proprii.
Variabilei discriminante (Z1) ii va corespunde cel mai mare raport de corelatie R(Z1,Y) si este asociata celei mai mari valori proprii. Cea de-a doua variabila discriminanta (Z2) necorelata cu prima cor(Z1,Z2)=0 , corespunde celei de-a doua valori proprii, iar raportul de corelatie dintre (Z2) si variabila de explicat Y, respectiv R(Z2,Y) este mai mic decat in cazul primei variabile discriminante. Deci variabilele discriminate nu sunt corelate intre ele.
Pentru precizarea numarului de variabile discriminante ce trebuie luate in considerare se foloseste un test privind nulitatea ultimelor q rapoarte de corelatie. Pentru aceasta exista statistica lui Wilks
![]()

ipoteza este respinsa pentru valori mici ale lui λ.
Bartlett si Rao au propus diferite legi de aproximare a distributiei λq , care sa permita calcularea nivelului de semnificatie.
Astfel Bartlett a considerat ca statistica
 ar putea fi aproximata cu o lege χ2 cu
q(k-1) grade de libertate. Aceasta aproximare este folosita mai ales
in cazul in care numarul de clase k este mai mare decat 2 sau 3.
ar putea fi aproximata cu o lege χ2 cu
q(k-1) grade de libertate. Aceasta aproximare este folosita mai ales
in cazul in care numarul de clase k este mai mare decat 2 sau 3.
Deci statistica lui Wilks masoara puterea globala de discriminare a noilor variabile. Cu cat λ inregistreaza o valoare mai mica cu atat este mai mare puterea discriminare a axelor. Acele variabile de discriminare Zm care au puterea de discriminare scazuta nu prezinta interes pentru a fi luate in considerare.
Pentru ca axele discriminante (Z) sa poata fi interpretate din punctul de vedere al semnificatiei statistice, trebuie studiata legatura dintre ele si variabilele explicative. Aceasta se poate realiza cu ajutorul:
Coeficientilor functiilor, care se interpreteaza ca pondere a variabilelor explicative in formarea axelor
Coeficientii de corelatie dintre axa discriminanta si fiecare variabila explicativa, care vor pune in evidenta variabilele cu care sunt cel mai bine corelate axele discriminante.
Variabilele discriminante sunt utilizate pentru repartizarea unitatilor in grupe, pe baza unei reguli de discriminare. Aceasta regula de decizie este usor de stabilit atunci cand axele discriminate sunt cel mult doua, in celelalte situatii, elaborarea ei este foarte dificila. Intr-o astfel de situatie se recomanda calcularea probabilitatilor de apartenenta la diferitele grupe, respectiv:
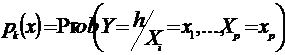
In ipoteza ca vectorul X al variabilelor explicative (X1 ,X 2,, Xp) urmeaza o lege de distributie multi-normala N(μh, ρ) pe fiecare subpopulatie (fiecare grupa), probabilitatile se determina astfel:

Variabilele gh (x) sunt denumite functii discriminante
si sunt estimate prin ![]() , unde:
, unde: ![]() =
= ![]() ;
; ![]()
Probabilitatea ph(x) fiind estimata prin:
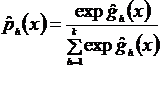
Fiecare unitatea va putea fi repartizata intr-o grupa si anume in aceea pentru care se inregistreaza probabilitatea cea mai mare.
Utilizand aceasta regula de decizie optimala se pot
repartiza in grupele deja formate noile unitati pe baza nivelului
inregistrat de cele p variabile explicative (X1 ,X 2,,
Xp).avand functiile discriminate estimate se pot calcula
valorile inregistrate de acestea pentru fiecare noua unitate ce trebuie
repartizata intr-o grupa, respectiv:![]()
De asemenea se pot calcula
probabilitatile estimate  ,exprimand sansa noii unitati de a
apartine fiecarei grupe in parte. Noua unitate va fi repartizata in acea grupa pentru
care se inregistreaza probabilitatea cea mai mare.
,exprimand sansa noii unitati de a
apartine fiecarei grupe in parte. Noua unitate va fi repartizata in acea grupa pentru
care se inregistreaza probabilitatea cea mai mare.
Pentru aprecierea eficientei regulii de decizie stabilita se compara situatia initiala de repartizare a unitatilor in grupe cu situatia rezultata in urma utilizarii functiilor discriminante, respectiv se construieste asa numita matrice a confuziilor, de urmatoarea forma:
|
Grupare dupa regula |
Grupare initiala 2 . k |
Total |
|
k |
|
|
|
Total |
|
|
Se calculeaza un asa numit scor discriminant obtinut prin raportarea numarului de unitati ce coincid in ambele grupari la numarul total de unitati de grupat, respectiv:
![]()
Cu cat acest scor este mai aproape de valoarea 1 cu atat gruparea unitatilor folosind functiile discriminate devine mai eficienta.
4 "Functia scor" -modele economice consacrate
Metoda scorurilor a fost aplicata pentru prima data in SUA pentru predictia falimentului. Acesta este si domeniul in care a fost utilizata cu succes, dand nastere unor modele viabile care se bazeaza pe cunoasterea anumitor rate pentru detectarea riscului de faliment al unei intreprinderi.
Aceste metode permit realizarea unui clasament alcatuit dintr-o combinatie liniara de rate financiare (functie scor(Z)). Un model de functie scor include de la 5 la 8 rate (rate economico financiare - in cazul unei analize financiare), bine selectionate in urma aplicarii procesului analizei discriminante. Trebuie subliniat faptul ca utilizarea acestor modele este limitata deoarece ele au fost dezvoltate intr-o anumita perioada istorica, pe baza datelor culese in acele momente. Astfel, rezultatele utilizarii unui model clasic trebuie sa fie insotite si de alte instrumente de analiza economico-financiara, inainte de a fi luata o decizie, dar sunt un semnal cu privire la situatia economica si financiara a societatii .
Metoda scorurilor se bazeaza pe un calup de rate (indicatori) determinati statistic care ponderati cu anumiti coeficienti in cadrul unui model matematic pot determina cu o anumita probabilitate starea de sanatate viitoare a intreprinderii. Astfel, se atribuie intreprinderii analizate o nota Z numita "scor" care este o combinatie liniara de rate:
Z = a1R1+a2R2+a3R3+.anRn, unde
R1, R2, R3.Rn reprezinta valorile diverselor rate
A1,a2,a3 reprezinta coeficientii afectati ratelor
In functie de valoarea scorului, intreprinderea este prezumata sanatoasa sau falimentara.
Din punct de vedere tehnic, determinarea scorului necesita parcurgerea urmatoarelor etape (aceleasi ca si in cazul Analizei Discriminante Liniare):
Se alege un esantion aleatoriu de intreprinderi de dimensiuni si activitati comparabile din care un grup sa includa intreprinderi falimentare sau aflate in dificultate (de exemplu cu mari probleme in achitarea obligatiilor) si un grup care sa includa intreprinderi sanatoase (cu indicatori favorabili de lichiditate, solvabilitate, rentabilitate);
In cadrul esantionului ales se procedeaza la compararea valorilor unor indicatori susceptibili a fi semnificativi cu starea de faliment sau non-faliment a intreprinderilor. In acest sens se cauta a defini o functie discriminanta Z = a x R + b, dand lui z o valoare 0 daca intreprinderea este falimentara si 1 daca intreprinderea este sanatoasa.
Se testeaza puterea discriminatorie a ratei R printre mai multe rate posibile. In acest sens se utilizeaza diferite teste statistice rezultand in final indicatorii cu actiune permanenta si puternica in cadrul esantioanelor cercetate:
Elaborarea prin tehnica analizei discriminante a unei combinatii liniare Z a indicatorilor determinanti.
Alegerea unui punct (sau puncte) de inflexiune care sa realizeze o clasificare predictiva a intreprinderilor din esantion din punct de vedere a riscului de faliment care le ameninta.
Determinarea probabilitatii de faliment pentru o anumita valoare Z. Probabilitatea de faliment, corespunzator unui interval Z dat este egala cu raportul dintre numarul de intreprinderi falimentare si numarul total de intreprinderi (falimentare si sanatoase) ale intervalului. Pe baza unor calcule matematice (utilizand densitatile de probabilitate) va rezulta o probabilitate de faliment pentru fiecare valoare a lui Z. In practica se poate considera ca o intreprindere este considerata falimentara daca probabilitatea sa de faliment este superioara lui 65 % si este prezentata ca sanatoasa daca posibilitatea de faliment este inferioara de 35 %;
Analiza apriori a scorului Z prin compararea valorilor obtinute a lui Z cu situatia concreta de faliment sau non-faliment in care s-a incadrat intreprinderea.
Analiza aposteriori a scorului Z pentru a testa starea de sanatate financiara a unui alt esantion de firme.
Intre modelele cele mai cunoscute amintim: modelul Altman, modelul Canon-Holder, modelul Bancii Centralei Frantei, modelele "F", "A" si "I", ale economiei romanesti.
Acad. Florin Gheorghe FILIP, Decizie asistata de calculator metode si tehnici de asistare a deciziilor centrate pe judecata umana, Revista Informatica Economica, nr. 4 (3)/2000
Ludovic LEBART, Alain MORINEAU, Marie PIRION Statistique exploratoire multidimensionnelle , Ed Dunod, Paris, 1995
Anuta Buiga , Metodologie de sondaj si analiza datelor in studiile de piata, Presa Universitara Clujeana, Cluj-Napoca,
Mireille BARDOS, Analyse Discriminante Aplication au risque et scoring financier, Dunod, Paris, 2001
Mireille BARDOS , Analyse Discriminante Aplication au risque et scoring financier, Dunod, Paris, 2001
Mireille BARDOS Analyse Discriminante Aplication au
risque et scoring financier, , Dunod,
Mireille BARDOS , Analyse Discriminante Aplication au risque et scoring financier, Dunod, Paris, 2001
Cristian DRAGOS, Elemente de econometria variabilelor calitative cu aplicatii in finante, Ed Presa Universitara Clujeana, 2006
Anuta BUIGA, Analiza discriminanta si aplicatiile ei in economie, Studia Universitatis , Babes-Bolyai, Oeconomica, XLVII, 1, 2002
|
Politica de confidentialitate |
| Copyright ©
2026 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |