
Arbori de decizie si retele neuronale
1 Notiuni introductive de data-mining
Data mining, metoda numita si Cunoastere - Descoperire in baze de date (Knoledge - Descovery in Data Mining, KDD)[1], este o noua disciplina care se afla la intersectia dintre statistica , baze de date, recunoasterea tiparelor, invatarea automata si alte domenii . Se axeaza pe o analiza secundara a bazelor mari de date cu scopul se a gasi relatii anterior nebanuite, care prezinta interes sau valoare pentru utilizator.
Data mining este un proces analitic[4], destinat sa analizeze informatii (de obicei legate de activitati economice sau de piata ), in cautarea unor tipare sau relatii sistematice intre variabile si apoi sa valideze ceea ce au gasit, aplicand tiparele identificate pentru noi seturi de date. De obicei seturile de date sunt mari ca numar de inregistrari, dar si variabilele independente sunt numeroase. Scopul final al acestor tehnicilor este previziunea[6] - iar data mining-ul previzional este si cel mai cunoscut tip de data mining si cu cele mai multe aplicatii economice (aceste metode au fost aplicate pentru selectarea de portofolii, credit - scoring, detectarea de fraude si cercetari de piata ).
Procesul de data mining are trei etape: (1)analiza initiala,(2) constructia modelului sau identificarea tiparului (inclusiv verificarea) si (3)aplicarea modelului la un nou set de date pentru a genera previziuni.
Tehnica data - mining-ului identifica prin modelare ceea ce nu este vizibil sau ceea ce se va intampla, adica prin crearea unui model pentru o situatie in care raspunsul se cunoaste si aplicarea acestuia la o alta situatie, necunoscuta. Softul utilizat este cel care selecteaza caracteristicile care sa intre in model (cele relevante pentru situatia existenta). Dupa ce modelul a fost realizat, acesta se poate aplica pentru o alta situatie asemanatoare . Verificarea modelului, a validitatii acestuia si a capacitatii sale de predictie, se poate face prin scoaterea anumitor observatii din procesul de data - mining si testarea modelului obtinut pe datele care au fost retinute. Cand instrumentele de data-mining sunt puse in fata unor date intre care exista relatii complexe , instrumentele pot fi invatate sa identifice aceste relatii.
Avantajul principal pe care aceste metode il au fata de metodele statistice clasice de analiza datelor consta in faptul ca ele pot utiliza datele pentru a obtine rezultate viabile chiar si atunci cand relatia dintre variabilele dependente si cele independente este neliniara si cand forma specifica a acesteia este necunoscuta.
Cele mai utilizate tehnici de data - mining sunt :
¤Retelele neuronale artificiale - modele de previziune non-liniare care invata in cadrul procesului de invatare si se aseamana cu retelele neuronale biologice ca structura
¤Arborii de decizie - structuri in forma de arbore care reprezinta seturi de decizii. Aceste decizii genereaza reguli de clasificare a datelor. Intre cele mai cunoscute metode includem Arborii de clasificare si de regresie (CART) si Detectarea automata a interactiunilor hi-patrat (CHAID)
¤Algoritmii genetici - tehnici de optimizare care se bazeaza pe procese de natura recombinarilor genetice, a mutatiilor, a selectiei naturale .
¤Metoda vecinilor celor mai apropiati - o tehnica de clasificare a fiecarei inregistrari pe baza unei combinatii a claselor obtinute pentru K inregistrari (din setul istoric de date), cele mai asemanatoare cu cea in cauza
¤Inducerea de reguli - extragerea de reguli utile de tipul "daca - atunci" din setul de date, pe baza semnificatiei statistice
Multe din aceste tehnici sunt utilizate de mai mult de zece ani iar acum evolueaza spre a fi integrate direct impreuna cu depozitele de date standardizate si platformele OLAP.
O comparatie intre diversele metode de data - mining nu este posibila deoarece fiecare metoda are scopuri diferitei si alte circumstante de aplicare . De asemenea, fiecare tehnica de data - mining se bazeaza pe anumite ipoteze, are anumite limite si se poate aplica doar in anumite cazuri.
Dintre utilizatorii acestor metode amintim: retelele de vanzari, companiile de carduri de credit, companiile de transport, companiile farmaceutice.domenii in care volumul de date este mare.
In continuare sunt detaliate doua dintre aceste metode, arborii de decizie si respectiv retelele neuronale, urmand ca acestea sa se regaseasca si sub forma de aplicatie practica din capitolul urmator.
2 Arbori de decizie
Arborii de decizie fac parte din tehnicile non-parametrice, fiind numiti dupa caz, arbori de decizie, de clasificare sau de segmentare. Acesti arbori utilizeaza variabile calitative, cantitative sau combinat si sunt folositi de mai multe sisteme data mining.
Aceasta tehnica consta intr-un mod de reprezentare a unei serii de reguli care conduce la o valoare sau la o clasa de valori. Asa cum reiese si din denumire, se construieste o structura de tip arborescent care reprezinta un set de decizii utilizate pentru a prezice care inregistrari dintr-un esantion nou vor avea anumite valori sau vor fi repartizate intr-o anumita clasa.
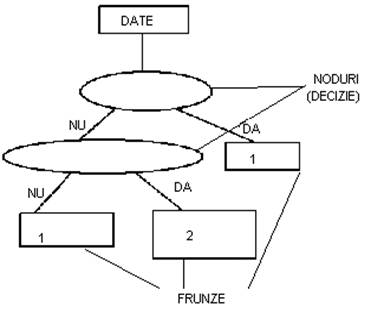
Intr-un arbore, nodurile interioare corespund variabilelor, ramificatia spre un nod fiu reprezinta o posibila valoare pentru acea variabila, iar o frunza reprezinta o valoare a variabilei tinta[10].
Avantajele arborilor de decizie [11]:
pot fi intelese de orice utilizator (lizibilitatea rezultatelor - regulilor - arborelui)
justificarea unei anumite clasificari (radacina -> frunza)
toate tipurile (categoriile) de variabile
arborele alege singur variabilele discriminante
nu sunt influentati de valori lipsa sau aberante (extreme)
variabilele independente apar in ordinea importantei
clasificare rapida
indica in mod clar care variabile sunt cele mai importante pentru clasificare
instrument disponibil in cea mai mare parte a programelor de data mining
sunt o cutie alba (conditia este usor de explicat cu ajutorul logicii booleene)
modelul poate fi validat cu ajutorul testelor statistice
sunt robuste, pot analiza cantitati mari de date intr-un scurt timp
Dezavantaje principale ale acestor tehnici :
sensibili la numarul de clase
evolutia in timp : daca variabilele evolueaza in timp este necesara reluarea fazei de invatare
Exista mai multi algoritmi[12] care pot fi utilizati: CART, C4.5, NewId, ITrule, CHAID, CN2 etc. Totusi, cele mai importante metode sunt CART (model de clasificare si regresie dihitomic) si C4.5 (model de clasificare cu un numar nelimitat de ramuri). Pentru usurinta aplicarii acestor metode au fost create programe soft speciale.
Se pot construi si "paduri aleatoare"(random forests), care presupun utilizarea mai multor arbori pentru a imbunatatii rata clasificarii corecte.
In continuare voi prezenta aspectele principale cuprinse in metoda de clasificare bazata pe arborii CART[13].
Tehnica CART, dezvoltata de H.Breiman, presupune atat arbori de clasificare (valoarea previzionata reprezinta clasa careia ii apartine inregistrarea), si arbori de regresie (valoarea previzionata poate fi orice numar real). Aceasta tehnica este utilizata pentru clasificarea unui set de date. Ea presupune un set de reguli care se aplica la noi seturi de date (neclasificate) pentru a prezice care inregistrari vor avea un anumit rezultat dat.
Diferenta majora fata de tehnica CHAID este ca variabilele independente pot fi continue. In plus, CHAID este un tip de arbore nebinar, utilizat mai ales in marketing (studii de segmentarea pietei), care se bazeaza pe testul hi-patrat.
In cazul arborilor CART, decizia este dihotomica (cu doua variante de raspuns) si deci se vor obtine doua segmente fiu, iar ramificarile si fuziunile se bazeaza pe o masura de omogenitate intre segmentele formate. In determinarea arborelui de clasificare trebuie specificat criteriul pentru masurarea acuratetei predictiei, trebuie selectate o metoda de partitionare si un criteriu de oprire.
Din moment ce toate inregistrarile din esantion sunt incadrate in clasele corespunzatoare anterior aplicarii acestei tehnici, procesul de constructie a arborilor de decizie face parte din invatarea supervizata. Aceasta metoda mai este numita si "divide si cucereste"[14], iar arborele va fi realizat de sus in jos.
Constructia unui arbore de decizie presupune mai multe etape, dupa cum urmeaza.
Pentru a imparti n indivizi in 2 grupuri cu ajutorul a p caracteristici (variabile explicative) , acestea sunt analizate succesiv si, cu ajutorul unui punct critic (prag) se retin acele caracteristici care separa cel mai bine cele doua grupuri .Punctul critic separa cele doua populatii initiale cu ajutorul unei intrebari la care se raspunde cu "da" sau "nu". Subgrupurile care nu se mai divid se numesc noduri terminale sau frunze.
Scopul acestei metode este de a se obtine in fiecare nod terminal o populatie cat mai omogena posibil. Astfel, ipoteza dorita este aceea in care un nod terminal contine elemente dintr-un singur grup. Cealalta posibilitate, este aceea in care "frunza" contine o mixtura a doua grupuri, din care unul predomina. Nodul terminal va fi atunci repartizat in acea grupa (unica, respectiv dominanta).
Este posibil ca mai multe noduri terminale sa fie repartizate aceluiasi grup. Fiecare nod terminal este caracterizat de un ansamblu de conditii care corespund pragurilor critice succesive care definesc etapele ce duc la acel nod terminal.
In interiorul arborelui fiecare sub-ansamblu definit de o valoare critica se numeste nod.
Construirea unui arbore se realizeaza prin[15]:
- Determinarea pragurilor critice succesive
- Decizia la nivelul fiecarui nod - daca sa continue algoritmul sau sa considere acel nod ca fiind terminal
- Incadrarea fiecarui nod terminal intr-o clasa
Pentru a realiza aceasta constructie trebuie utilizat un algoritm. Adica la fiecare pas se va alege cel mai bun prag critic, ceea ce presupune o masura a calitatii. Se formeaza o succesiune de noduri, fiecare din ele avand doua ramuri care impart populatia identificata la nivelul acelui nod in doua subpopulatii. Arborele creat astfel se numeste arbore maxim. Problema care se pune este daca acesta este optim pentru discriminare si in consecinta se cauta nu o regula optimala, ci eficienta.
Astfel, la nivelul fiecarui nod trebuie determinat[16]:
un criteriu de clasificare (o intrebare cu raspuns dihotomic) - raspunsul "da" corespunde ramurii din stanga a arborelui, iar raspunsul "nu" corespunde ramurii drepte a acestuia
o metoda de masurare a calitatii pragului, pentru a repartiza cat mai bine inregistrarile la fiecare dintre pasi
un criteriu de oprire a constructiei arborelui
o regula de clasificare a fiecarui nod terminal
In ceea ce priveste metoda CART, ideea de baza este aceea de a alege la fiecare nod un prag care sa duca in continuare la noduri cat mai "pure" posibil (cat mai putin amestecate, in orice caz mai pure decat nodul parinte).
Avand o regula de clasificare pentru fiecare nod terminal, puterea discriminanta a arborelui se poate masura prin proportia totala a clasamentelor corecte.
Criteriul de clasificare (Pragul) :
La fiecare nod trebuie gasita o conditie care imparte esantionul, iar acest test trebuie sa fie un atribut.
In functie de tipul variabilelor observate (variabilele explicative), pragul critic corespunde diferitelor forme de intrebari.
Daca variabila este numerica continua, pentru o variabila x intrebarea este de forma "este x <= c?
Daca variabila este ordinala cu m clase, atunci exista m-1 posibilitati.
Daca variabila este nominala, atunci exista 2 m-1 posibilitati de repartizare in doua grupuri.
Masurarea calitatii pragului :
Regula generala poate fi formulata astfel[17]: atributul trebuie sa imparta esantionul astfel incat subseturile rezultate sa contina inregistrari care sa apartina aceleiasi clase sau sa se apropie de aceasta conditie cat mai mult.
Se pot utiliza mai multe criterii de minimizare a numarului de elemente care apartin altor clase (a impuritatii), dintre care cele mai importante sunt:
Criteriul informatiei (Information-theoretical criterion), utilizat de algoritmul C4.5
![]() (1)
(1)
unde Info(T) este entropia setului T si
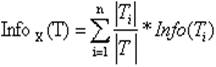 (2)
(2)
unde seturile T1, T2, . Tn se obtin prin impartirea setului initial prin testul t.este selectat atributul care produce valoarea cea mai mare avand in vedere criteriul (1).
Criteriul statistic, utilizat de algoritmul CART, indexul Gini, care estimeaza distanta dintre probabilitatea de distributie a claselor.
Cu ajutorul indexului Gini vom masura calitatea clasificarii realizate la un nod si apoi puterea de discriminare a unui arbore si vom identifica impuritatea care caracterizeaza gradul de combinare a nodului sau a nodurilor terminale ale arborelui. Acesta ajunge la minimul sau atunci cand toate inregistrarile dintr-un nod sunt din aceeasi categorie .
Daca nt este numarul de indivizi care au intrat intr-un nod t, acesta avand ca si noduri fiu ts respectiv td si presupunand ca numarul de grupe de clasificat este J, putem scrie:
![]()
Respectiv:  si
si 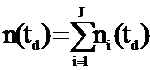
In aceste conditii algoritmul urmareste minimizarea impuritatii ( Δi):
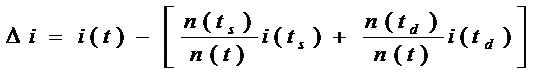
Impuritatea i(t) este o functie de probabilitate de apartenenta la o grupa j stiind ca la nodul t : i(t)=Φ(p(1/t p(2/t p(J/t) ), unde p(j/t) este probabilitatea de a apartine grupei j. Impuritatea trebuie sa satisfaca urmatoarele proprietati:
- sa fie o functie simetrica de p(j/t), unde j=(1,2,.J)
- sa fie minima daca nodul este pur
- sa fie maxima daca combinarea inregistrarilor este perfecta
Arborele T este caracterizat de totalitatea nodurilor sale terminale, notate pe caz general T . Impuritatea arborelui este astfel este data de:
![]() Daca se doreste
minimizarea impuritatii pragurilor critice, trebuie minimizata
impuritatea intregului arbore, iar pentru aceasta se utilizeaza algoritmul
"variabila cu variabila". Se incepe prin identificare pragului critic
care minimizeaza impuritatea (pentru fiecare variabila), apoi dintre
toate cuplurile (variabila, prag) se alege acela care minimizeaza impuritatea.
Daca se doreste
minimizarea impuritatii pragurilor critice, trebuie minimizata
impuritatea intregului arbore, iar pentru aceasta se utilizeaza algoritmul
"variabila cu variabila". Se incepe prin identificare pragului critic
care minimizeaza impuritatea (pentru fiecare variabila), apoi dintre
toate cuplurile (variabila, prag) se alege acela care minimizeaza impuritatea.
Regula de oprire a arborelui:
Daca algoritmul este urmat pana cand nodurile terminale sunt pure sau pana cand impuritatea nu mai scade, nodurile terminale vor fi numeroase si multe dintre acestea vor contine prea putini indivizi .
Un astfel de arbore maximal poate sa nu mai aiba putere. Astfel este necesara specificarea unei proceduri de oprire a arborelui. Pentru a limita ramificatiile inutile se utilizeaza mai multe criterii si arborele va fi oprit in cazul in care este pur, daca impuritatea a scazut sub nivelul precizat de un anumit prag ( it< i0 ), daca variatia impuritatii este prea mica (inferioara unui prag), daca numarul de indivizi care sunt repartizati unui nod este prea mic fata de un anumit nivel (nt< n0), .
Totusi, autoritatile din domeniu recomanda nu oprirea arborelui ci "taierea"[19] acestuia (pruning), deoarece altfel se obtin modele de clasificare prea putin exacte.
Spre deosebire de procesul constructiei, cel de taiere merge de jos in sus transformand nodurile in frunze sau inlocuindu-le cu sub-arbori.
Chiar si simplificati prin taiere, uneori arborii pot fi greu de inteles. De aceea se poate apela la extragerea regulilor din arbore, urmand pe rand fiecare cale de la radacina pana la frunza arborelui.
Validarea unui arbore:
Calcularea proportiei clasamentelor corect realizate reprezinta o masura a calitatii puterii de discriminare a arborelui. De cele mai multe ori se utilizeaza un esantion test. Daca insa nu se dispune de date , pentru a permite utilizarea acestei metode de validare, se poate utiliza validarea incrucisata. Cu ajutorul acestor metode se poate identifica un arbore eficace.
Metoda esantionului test presupune impartirea esantionului initial intr-un esantion de invatare si unul test . Pe baza primului se construiesc arborii iar cu ajutorul celui din urma se exerseaza, se calculeaza riscul clasificarilor gresite si se retine acel arbore care minimizeaza acest risc.
Cea de-a doua metoda pleaca de la un arbore eficace T(α) construit si pentru a-i estima riscul imparte populatia E prin trageri aleatoare in V subpopulatii de volum egal .
Notam Ev un astfel de esantion, iar E(v) complementarul lui Ev, (adica E(v)=1- Ev ) .Pentru fiecare E(v) si pentru fiecare α se construieste un arbore eficient T(v) α.
Riscul arborelui T(v) α este:
![]()
Pentru diferite valori ale lui α riscurile sunt comparate si este considerat ca fiind cel mai bun arborele cu cel mai mic risc.
Intre domeniile cu un camp de aplicare larg al acestei metode se numara medicina, industria, controlul calitatii, biologia moleculara, analiza compozitiei amino-acizilor, estimarea riscului de creditare si analiza financiara.
3 Retelele neuronale
O diferenta cheie intre retelele neuronale si oricare alta tehnica de data - mining este aceea ca retelele neuronale opereaza numai direct pe numere. Rezulta ca orice data ne-numerica din coloanele independente trebuie convertita in numar inainte sa putem folosi datele intr-o retea neuronala.
Din punct de vedere structural o retea neuronala este un ansamblu de unitati interconectate (neuroni) fiecare fiind caracterizata de o functionare simpla. Functionarea unitatilor este influentata de o serie de parametrii adaptabili. Astfel o retea neuronala este un sistem extrem de flexibil. Structura unitatilor functionale, prezenta conexiunilor si a parametrilor precum si modul de functionare sunt inspirate din creierul uman.
O retea neuronala artificiala este un ansamblu de unitati functionale amplasate in nodurile unui graf orientat. De-a lungul arcelor grafului circula semnale care permit unitatilor functionale sa comunice intre ele.
Retelele neuronale nu sunt eficiente pentru orice problema, ele fiind utilizate in rezolvarea problemelor pentru care se dispune de un numar mare de exemple si pentru care nu pot fi gasite usor si rapid reguli de normalizare. De exemplu,pot fi utilizate cu succes pentru[20]:
¤ clasificari (clasificarea speciilor de animale pe baza analizei ADN)
¤ recunoasterea motivelor (recunoasterea optica a caracterelor( OCR) de catre banci sau posta )
¤ aproximarea unei functii necunoscute
¤ modelarea unei functii cunoscute, dar prea complexa pentru a fi calculata cu exactitudine (decodarea semnalelor satelitilor si transformarea lor in date la suprafata marii)
¤ estimatii la bursa de valori (aprecierea valorii unei intreprinderi, previziunea periodicitatii cursului bursier)
Abilitatea unei retele neuronale de a rezolva o anumita problema este influentata si de modul in care sunt pregatite datele de intrare. Aceste trebuie prelucrate atent, pentru ca altfel demersul rezolvarii problemei cu retele neuronale poate fi sortit esecului.
Utilizatorii trebuie sa fie constienti insa si de urmatoarele probleme:
retelele neuronale sunt ca o cutie neagra, nefiind furnizate nici o explicare a rezultatelor;
in general, retelele neuronale necesita un timp indelungat de invatare; totusi, odata invatate, ele pot prezice destul de repede rezultatele;
retelele neuronale necesita o pregatire minutioasa a datelor, au nevoie de cazuri reale ca si exemple pe baza carora sa "invete" (cu cat problema este mai complexa, cu atat acestea trebuie sa fie mai numeroase);
retelele neuronale se preteaza foarte bine rezolvarii problemelor complexe;
Neuronul -
Un neuron reprezinta unitatea de calcul elementar a retelelor neuronale, formata dintr-un set de variabile de intrare (xi) carora le sunt asociate ponderi ; o functie (f) care insumeaza ponderile si prezinta rezultatul sub forma de output (y) .
Vectorul intrare X este transformat intr-o variabila de iesire Y printr-un produs scalar si o functie de transformare neliniara[22]:
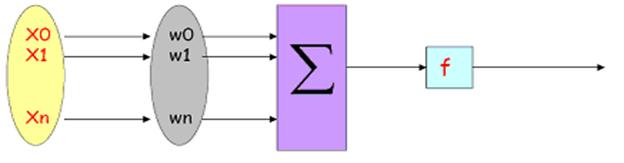
vectorul ponderea w suma functie iesire y
de intrare X a vectorului ponderata de activare
(coeficienti sinaptici)
Fiecarei sinapse ii este asociata o pondere w, astfel ca neuronii nivelului anterior se multiplica cu acele ponderi si apoi se aduna la neuronii nivelului respectiv, ceea ce este echivalent cu a multiplica vectorul intrare cu o matrice de transformare. Dincolo de aceasta structura simpla, reteaua poate de asemenea sa contina bucle care schimba complet variantele posibile, dar si complexitatea creste[23].
Exista patru tipuri de conexiuni ponderate[24]:
Feedforward connections - in cazul tuturor modelelor, de la un nivel la urmatorul
Feedback connections - in sens invers fata de conexiunile feedforward
Lateral connections permit interactiunea neuronilor pentru pastrarea unei relatii topologice
Time-delayed connections - sunt utile in cazul recunoasterii paternurilor temporale si a modelelor dinamice.
In perioada de inceput a utilizarii retelelor neuronale functia de activare utiliza doar codul binar, in functie de puterea semnalului (daca depasea sau nu o valoare critica);in prezent insa , se utilizeaza functia sigmoida (care poate lua valori intre 0 si 1 sau intre -1 si 1).Semnalul modificat este apoi trimis spre neuronii de iesire, care aplica de asemenea functii de activare. Astfel, informatia cu privire la paternul invatat este codificata in semnalele care sunt transmise spre si de la noduri. Aceste semnale exprima relatia dintre nodurile de intrare (variabilele independente) si cele de iesire (variabila dependenta).
Functia de activare poate lua una dintre formele urmatoare[25]:
Functia tangenta hiperbolica: = ![]()
Functia logistica: = 
Functia sigmoida: = 
Aceasta din urma ia valori intre 0 si 1 (atat la intrare cat si la iesire).
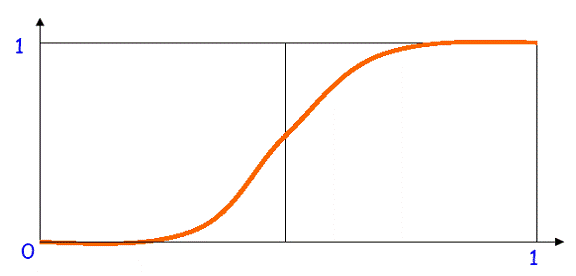
Functia de activare prezinta in general trei intervale[26]:
¤Sub prag - neuronul este inactiv iar iesirea ia valoarea 0 (sau -1 )
¤in jurul pragului - o faza de tranzitie
¤peste prag - neuronul este activ iar iesirea este 1 de obicei
In cazul neuronilor umani, pe care retelele neuronale incearca sa le imite, s-au pus in evidenta urmatoarele:
timpul de trecere de la un neuron la altul 10-3 sec
numarul de neuroni
numar de sinapse (conexiuni)/neuron
In cazul retelelor artificiale numarul de neuroni, respectiv sinapse difera de la un caz la altul, in functie de complexitatea datelor de intrare.
Niveluri -
Neuronii sunt organizati pe mai multe niveluri:

Nivelul de intrare (imput layer) este format nu din neuroni, ci mai degraba din simple valori din baza de date si reprezinta imputuri pentru urmatorul nivel de neuroni.
Urmatorul nivel se mai numeste si nivelul ascuns (hidden layer); pot fi mai multe astfel de niveluri. Rolul nivelului ascuns este acela de a procesa informatia primita de la nivelul de intrare. Numele acestuia este dat de faptul ca acesta nu contine nici informatie initiala si nici finala, iar rezultatele acestuia de obicei raman ascunse utilizatorului.
Nivelul final este cel de iesire si se prezinta sub forma unui singur nod pentru fiecare clasa (output layer).
Reteaua -
Retelele neuronale pot fi definite ca si tehnici analitice modelate dupa procesul de invatare in cadrul sistemului cognitiv si a functiilor neurologice ale creierului , capabile sa previzioneze noi observatii (pentru anumite variabile) pe baza altor observatii (pentru aceleasi sau alte variabile) dupa realizarea procesului asa-zis de invatare pe baza datelor existente .
Exista mai multe tipuri de retele neuronale, diferenta dintre ele fiind data de mai multi parametrii:
Tipologia conexiunilor dintre neuroni
Functia de agregare utilizata (suma ponderata, distanta pseudo-euclidiana)
Functia de activare utilizata (sigmoida, liniara, Gauss)
Algoritmul de invatare (retro-propagarea erorii, corelatia in cascada)
Metoda degradarii ponderilor
(weight decay) care permite evitarea super-invatarii De obicei se utilizeaza suma
ponderata non-liniara (unde K reprezinta o functie
predefinita): 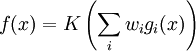
Alti parametrii specifici anumitor tipuri de retele
Cele mai cunoscute tipuri de retele neuronale sunt[28]:
Feedforward neural networks
Sunt primele si cele mai simple tipuri de retele neuronale. In cadrul lor informatia merge intr-un singur sens, de la neuronii de intrare prin cei ascunsi (daca exista) spre cei de iesire. Reteaua neuronala cu un singur nivel ascuns este cea mai cunoscuta, una dintre primele care au fost dezvoltate, a carei eficienta a fost stabilita si pentru care exista softuri corespunzatoare.
Single layer perceptron
Acest tip de retea este mai simpla
si presupune un singur nivel de iesire. Imputurile sunt transmise
direct spre outputuri printr-o serie de ponderi. Suma produselor dintre ponderi
si valoarea imputuri se calculeaza pentru fiecare nod si
daca valoarea este peste un anumit prag, atunci neuronul se activeaza
si ia valoarea 1, altfel ia valoarea dezactivata, 0. In cazul in care
se alege o functie logistica (sigmoida), reteaua cu un
singur nivel (single layer), este identica cu regresia logistica. Se
prefera aceasta functie ![]() si pentru ca este foarte usor de
calculat derivata sa: y' = y(1
− y)
si pentru ca este foarte usor de
calculat derivata sa: y' = y(1
− y)
Multi-layer perceptron
Aceasta tehnica utilizeaza invatarea supervizata[29], ceea ce inseamna ca foloseste o variabila tinta si modeleaza o functie care va fi utilizata pentru a previziona variabila tinta. In cazul unei variabile tinta ordinale, va clasifica inregistrarile in grupele definite pentru variabila in cauza. Reteaua identifica caracteristicile datelor care pot fi utilizate pentru a grupa impreuna inregistrarile similare. In acest caz, fiecare neuron este conectat cu cei din nivelul urmator. De cele mai multe ori se aplica o functie sigmoida. Tehnica de invatare utilizata cel mai frecvent este propagarea inversa (back-propagation).
Alte tipuri de retele neuronale:
Simple recurrent network - este o varianta a retelei multi-layer perceptron, cu trei niveluri, la care se adauga un set de "inregistrari ale contextului" pentru nivelul de intrare. In aceste inregistrari se copiaza valorile anterioare ale unitatilor din nivelul ascuns si reteaua poate realiza predictii secventiale.
Hopfield network - retea neuronala recurenta in care toate conexiunile sunt simetrice.

Primul pas in construirea unei retele este crearea unei anumite arhitecturi (care presupune un anumit numar de niveluri , fiecare continand un anumit numar de neuroni - structura acestora fiind prezentata anterior ). Marimea si structura retelei trebuie sa corespunda realitatii. Din moment ce complexitatea fenomenului investigat nu este cunoscuta de la inceput, se fac mai multe incercari. Insa cu ajutorul softurilor existente, care aplica tehnici de inteligenta artificiala, rezultatele se obtin mai rapid, aceste programe gasind cea mai buna arhitectura a retelei.
Noua retea este supusa apoi procesului de training. In aceasta etapa neuronii aplica un proces iterativ variabilelor de intrare pentru a ajusta ponderile retelei cu scopul de a realiza previziuni optime.
Ceea ce este cel mai interesant la retelele neuronale este capacitatea de a invata, care in practica presupune:
Fiind data o anumita sarcina de rezolvat si o
clasa de functii F, invatarea inseamna utilizarea unui
set de observatii pentru a gasi ![]() care sa rezolve sarcina intr-un mod
optim.
care sa rezolve sarcina intr-un mod
optim.
Acest proces se realizeaza prin ajustarea puterii semnalului primit de la nodurile anterioare. Pe masura ce invata sa prognozeze mai bine valoarea tinta din tiparul de intrare, fiecare conexiune dintre neuronii de intrare si neuronii ascunsi, respectiv dintre neuronii ascunsi si neuronii de iesire creste sau descreste in intensitate.
Semnalul care patrunde in neuronii ascunsi este modificat de o functie numita functie "critica" sau de activare.
Acest lucru presupune definirea
unei functii cost ![]() in
asa fel incat pentru solutia optima f*,
in
asa fel incat pentru solutia optima f*, ![]()
![]() (nici
o alta solutie nu are un cost mai mic decat cea optima.)
(nici
o alta solutie nu are un cost mai mic decat cea optima.)
Functia cost C este importanta deoarece masoara cat
de departe suntem de solutia optima. Estimarea parametrilor
functiei se realizeaza prin minimizarea unei functii de
pierdere, de obicei minimizarea sumei patratelor erorilor (diferenta
dintre valorile calculate si cele observate ) din esantionul de invatare[31]. ![]() , unde xi
reprezinta valorice observare, iar xi' reprezinta valorice calculate.
, unde xi
reprezinta valorice observare, iar xi' reprezinta valorice calculate.
Privind procesul de invatare exista trei paradigme, fiecare cu un mod particular de desfasurare:
Invatarea supervizata
Presupune cunoasterea anterioara a problemei si se urmareste
gasirea unei functii f care
sa stabileasca corespondentele dintre x si y unde ![]() .
De obicei functia cost
utilizata este eroarea medie patratica, care incearca
sa minimizeze eroarea medie dintre output-ul retelei si valoarea
urmarita y, pentru toate perechile. Se intalneste in cazul
regresiei, a clasificarii.
.
De obicei functia cost
utilizata este eroarea medie patratica, care incearca
sa minimizeze eroarea medie dintre output-ul retelei si valoarea
urmarita y, pentru toate perechile. Se intalneste in cazul
regresiei, a clasificarii.
Invatarea nesupervizata
Presupune alocarea unor date x iar functia cost care trebuie minimizata poate fi orice functie dintre datele x si output-ul retelei.
Invatarea de intarire
De obicei in acest caz datele nu
sunt furnizate dar sunt generate de interactiunea dintre un agent si
mediu. La fiecare moment de timp agentul actioneaza (yt ) si mediul genereaza o
observatie x t si un cost instantaneu c t . Scopul este gasirea unui mod de
selectare a actiunilor astfel incat o anumita masura a costului pe termen lung sa fie
minima. Mai formal, mediul este modelat ca un proces de luare a deciziilor
Marcov, cu starile ![]() si actiunile
si actiunile ![]() cu urmatoarele distributii de
probabilitate: distributia instantanee a costurilor P(ct
| st), distributia observatiilor P(xt | st) si tranzitia P(st
+ 1 | st,at). Acest model de
invatare se intalneste in probleme de control, de jocuri si
alte actiuni de luare a deciziilor in mod secvential.
cu urmatoarele distributii de
probabilitate: distributia instantanee a costurilor P(ct
| st), distributia observatiilor P(xt | st) si tranzitia P(st
+ 1 | st,at). Acest model de
invatare se intalneste in probleme de control, de jocuri si
alte actiuni de luare a deciziilor in mod secvential.
Algoritmul de invatare cel mai intalnit este retro-propagarea erorii. Initial ponderile w sunt alese la intamplare, dupa care, eroarea Q este retro-propagata si ponderile sunt modificate pentru a minimiza erorile.
Mai intai se compara valorile obtinute cu cele reale, iar apoi erorile sunt transmise inapoi prin retea si corectate dupa importanta elementelor care au participat la realizarea acelor erori (ponderile care au dus la o eroare mare vor fi modificate mai mult decat cele care au dus la o eroare minima).
Acest algoritm parcurge toate observatiile din esantion intr-o ordine precizata sau aleatoare si se repeta de mai multe ori pentru a obtine ponderi care tind spre un optim. Aceste ponderi sunt cele care furnizeaza solutia problemei studiate. Pentru a ajusta ponderile se poate folosi o metoda non-liniara de optimizare numita "gradient descendent". Aceasta foloseste derivata functiei erorii si de aceea propagarea inversa nu se poate aplica decat in cazul functiilor de activare diferentiabile.
Pentru o functionare optima a retelei, trebuie controlate mai multe elemente: parametrul de invatare al retelei, ε; variabilele initiale; numarul de niveluri; numarul de neuroni care formeaza nivelul ascuns.
Reteaua nu trebuie sa fie prea complexa, pentru ca, daca contine prea multi parametrii, care trebuie sa fie determinati in cursul procesului de invatare, atunci isi pierde capacitatea de generalizare. Dar nu trebuie sa fie nici prea simpla, deoarece atunci se pierd corelatiile dintre date.
Coeficientul ε , care controleaza amplitudinile modificarilor erorilor din algoritmul de minimizare a acestora poate lua valori intre 0.5 si 0.0001 de obicei. Valoarea coeficientului care maximizeaza numarul observatiilor bine clasate si care minimizeaza suma patratelor erorilor din esantionul test este retinuta.
In ceea ce priveste variabilele initiale, se intampla de multe ori ca valorile inregistrate utilizate pentru invatare sa fie aproximative sau deviate de la cele reale. Daca obligam reteaua sa raspunda aproape perfect la acele exemple, vom obtine o retea influentata de valori eronate.
Pentru a evita "supra-invatarea" (ipoteza in care reteaua nu mai poate fi folosita pentru a genera previziuni pe baza unor noi esantioane), se scindeaza esantionul initial in esantion de invatare si esantion test. Cat timp eroarea obtinuta pentru cel de-al doilea esantion se diminueaza putem continua invatarea, altfel ne oprim.
Intr-o retea multilayer pot fi unul sau mai multe niveluri cu neuroni ascunsi . Acest numar este adesea asociat cu numarul de niveluri ale ponderilor [33].
Nivelul ascuns este cel responsabil pentru proprietatile retelelor neuronale, iar numarul neuronilor pe care ii contine da retelei capacitatea sa de generalizare. Astfel, pentru o performanta foarte buna trebuie determinat un numar optim de unitati ascunse.
Exista mai multe incercari de calcul a numarului necesar de neuroni ascunsi. Dar rezultatele sunt contradictorii si in practica se fac mai multe incercari (se mentine acel numar care corespunde erorii minime). Desi nu exista un algoritm unic, s-au conturat cateva reguli euristice :
daca eroarea pentru esantionul de invatare este mica, dar pentru cel de validare este mare, atunci reteaua nu generalizeaza. Acest lucru inseamna ca trebuie redus numarul de neuroni din nivelul ascuns.
daca eroarea corespunzatoare esantionului de invatare este mare, ar trebui incercat sa se includa mai multi neuroni ascunsi.
daca toate ponderile pentru conexiunile dintre neuroni sunt de aceeasi marime, numarul de neuroni este prea mic.
intotdeauna se pot adauga noi neuroni ascunsi, dar eroarea poate avea o alta cauza. Eroarea poate fi mare si in cazul datelor de intrare.
Dupa aceasta faza de "invatare "pe baza unui set de date existent, noua retea este pregatita pentru generarea de previziuni. Reteaua care a rezultat in urma procesului de "invatare" reprezinta un tipar detectat in cadrul datelor . Din aceasta perspectiva reteaua este echivalentul functional al unui model de relatii dintre variabilele din abordarea clasica de construire a unui model.
Totusi, spre deosebire de modelele clasice, in cadrul retelei acele relatii nu pot fi compuse asa cum sunt ele utilizate pentru a descrie relatiile dintre variabile (de exemplu "A este corelat cu B, dar doar pentru acele observatii in care valoarea lui C este mica iar a lu D este mare"). Unele retele neuronale pot duce la previziuni foarte precise; totusi, ele reprezinta o abordare tipic teoretica ("o cutie neagra").
In acelasi timp, retelele neuronale pot fi utilizate pentru a explora seturile de date cu scopul de a gasi variabile sau grupuri de variabile relevante. Rezultatele acestui proces pot fi apoi utilizate pentru constructia modelului. Totodata, acum exista softuri specializate care utilizeaza algoritmi complecsi pentru a gasi cele mai relevante variabile pentru procesul de constructie al modelului.
Unul dintre avantajele majore ale retelelor neuronale il reprezinta faptul ca, teoretic, ele sunt capabile sa aproximeze orice functie continua si astfel utilizatorul nu trebuie sa formuleze nici o ipoteza cu privire la forma modelului sau, pana la un punct, care variabile sunt importante.
Alte avantaje ale utilizarii metodei retelelor neuronale:
proportie de eroare in general buna
procedeu disponibil in cadrul softurilor de data mining
robusta (neinfluentata de "zgomote"), permite recunoasterea formelor
clasificare rapida
se poate combina cu ale metode : de exemplu arbore de decizie pentru alegerea variabilelor explicative
In ciuda tuturor avantajelor precizate, multi statisticieni sunt neincrezatori in ceea ce priveste aceasta metoda. Un motiv este acela ca sunt niste "cutii negre".
Din cauza complexitatii functiilor utilizate in aproximarile facute, softul utilizat nu da informatii despre natura relatiei dintre variabilele explicative si cea de explicat (sau tinta). Output - ul obtinut este de fapt o valoare previzionata .
In acelasi timp , forma functionala a relatiei dintre cele doua categorii de variabile nu este prezentata explicit si astfel puterea relatiei dintre variabilele dependente si cele independente (importanta fiecarei variabile) nu este de multe ori surprinsa.
Modelele clasice , ca si alte tehnici de data - minig cum ar fi arborii de decizie, ofera utilizatorului si o descriere functionala sau o harta a legaturilor dintre variabile.
In plus, retelele neuronale sunt caracterizate de:
o faza de invatare prea lunga
destul de multi parametrii (arhitectura, coeficienti sinaptici)
o putere redusa de explicare ("cutie neagra")
dificultatea incorporarii cunostintelor dintr-un domeniu
o evolutie lenta in timp (faza de invatare, faza de training)
Unii autori accentueaza faptul ca retelele neuronale utilizeaza sau este de asteptat sa utilizeze un numar mare de procese de calcul in paralel.
De exemplu, Haykin (1994) defineste retelele neuronale ca: "un proces masiv, realizat in paralel cu o tendinta naturala de a aduna cunostinte experientiale si de a le pregati pentru utilizare. Se aseamana cu creierul prin doua aspecte: - cunostintele se asimileaza de catre retea printr-un proces de invatare; - puterea conexiunilor dintre neuroni cunoscuta ca si ponderi sinaptice sunt utilizate pentru a inmagazina informatiile " .
Totusi, asa cum Ripley (1996) accentueaza, marea majoritate a aplicatiilor utilizand retelele neuronale folosesc un singur procesor iar o modalitate de imbunatatire a vitezei de lucru este nu numai aceea de creare de softuri care sa beneficieze de avantajul hardurilor multiprocesor , dar si aceea de construire de algoritmi de invatare mai eficienti.
Aplicatii tipice ale retelelor neuronale se intalnesc in diagnosticele medicale, (neurologie si psihologie), analiza datelor economice (marketing, analiza creditelor, previziunea vanzarilor), controlul proceselor de productie, robotica.In domeniul inteligentei artificiale, retelele neuronale au fost aplicate cu succes pentru recunoasterea sunetelor, analiza de imagini, fiind bazate pe estimatii statistice, optimizare si teoria controlului. Se pot utiliza si pentru aproximarea de functii,analiza regresiei, previziunea si modelarea seriilor de timp, clasificare, luare de decizii , procesarea datelor.
Poate ceea ce este cel mai atractiv la aceasta tehnica este posibilitatea ca intr-o zi sa se realizeze niste retele constiente. Totusi, aceasta tehnica obtine rezultatele cele mai bune doar atunci cand este integrata cu Artificial Inteligence, Fuzzy Logic, etc.
J. H DAVID, Data mining: Statistics and More?, The american statistician , vol 52, no 2, 1998, ,www.amstat.org/publications
Gilbert SAPORTA, Data Mining and Official Statistics, Quinta Conferenza Nationale di Statistica, ISTAT, Roma, 15 novembre 2000
Louise FRANCIS , Neural Networks Demystified,2001 www.casact.org/pubs/forum
Louise FRANCIS , Neural Networks Demystified, 2001, www.casact.org/pubs/forum
Kurt THEARLING, Ph.D, An Introduction to Data Mining, www.thearling.com
Louise FRANCIS , Neural Networks Demystified, 2001, www.casact.org/pubs/forum
Laboratoire d'Informatique Fondamentale de Lille, Fouille de données (Data Mining) - Un tour d'horizon -
TAE KYUNG SUNG, NAMSIK CHANG, AND GUNHELEE E , Dynamics of Modeling in Data Mining: Interpretive Approach to Bankruptcy Prediction
Decision trees -- general principles of operation, www.basegroup.ru/trees
Kurt THEARLING, Ph.D, An Introduction to Data Mining https://www.thearling.com
Mireille BARDOS Analyse Discriminante Aplication au risque et scoring financier, , Dunod, Paris, 2001
Mireille BARDOS Analyse Discriminante Aplication au risque et scoring financier, , Dunod, Paris, 2001
Decision trees -- general principles of operation, www.basegroup.ru/trees
Decision trees -- general principles of operation, www.basegroup.ru/trees
Laboratoire d'Informatique Fondamentale de Lille, Fouille de données (Data Mining) -Un tour d'horizon
Mireille BARDOS Analyse Discriminante Aplication au risque et scoring financier, Ed. Dunod, Paris, 2001
Louise FRANCIS , Neural Networks Demystified, 2001, www.casact.org/pubs/forum
Ludovic LEBART, Alain MORINEAU, Marie PIRION, Statistique exploratoire multidimensionnelle , Ed Dunod, 2004
Mireille BARDOS Analyse Discriminante Aplication au risque et scoring financier, , Dunod, Paris, 2001
Louise FRANCIS , Neural Networks Demystified,2001, www.casact.org/pubs/forum
|
Politica de confidentialitate |
| Copyright ©
2026 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |