
www.preferatele.com
Proiect
Literatura de specialitate mentioneaza doua principale concepte:
conceptul clasic
conceptul neoclasic
Conceptul clasic abordeaza dobanda ca un rezultat al interactiunii dintre cerere si oferta in care prima identifica necesarul de resurse financiare pentru derularea unei investitii, iar oferta concretizeaza resursele financiare realizate pe seama economiilor.
Deficientele acestui concept constau intr-o abordare statica, adica, nu se tine seama de influenta factorului timp, de cresterea complexitatii fenomenelor economice (aparitia companiilor multi si transnationale, fenomenul de globalizare, etc.), de modul in care se formeaza dobanda de ratele de schimb valutar, rata inflatiei etc.
Conceptul neoclasic incearca sa se adapteze noilor conjuncturi economice facand apel la noi termeni ca: productivitatea marginala a capitalului, implicarea inflatiei ca un fenomen de cvasipermanenta si influentare directa, nemijlocita asupra dobanzii si nu in ultimul rand asupra deciziilor investitionale ca si a metodelor de actualizare, ceea ce ii confera factorului de timp importanta si influenta necesara.
Calculul sumei finale pe care o are de primit creditorul are in vedere numai suma initiala, iar pentru perioadele urmatoare sa nu se cumuleze suma initiala cu valoarea dobanzii, deci pe parcursul duratei de imprumut suma initiala ramane aceeasi, nemodificata.
Formula uzuala este:
Δd = ![]()
in care:
Δd suma (volumul dobanzii de plata pentru valoarea ratei dobanzii);
K volumul creditului;
rds rata dobanzii simple;
t perioada de timp aferente creditului, exprimata in zile.
Se conosc trei proceduri de calcul referitoare la un an bancar:
procedura germana la care anul bancar are 360 de zile, iar luna bancara are 30 de zile;
procedura franceza la care anul bancar are 360 de zile, iar luna bancara este identica cu luna calendaristica;
procedura engleza la care anul bancar are 365 de zile, iar luna bancara coincide cu luna calendaristica.
Daca pentru mai multe perioade de timp suma initiala (volumul creditului, K) ramane neschimbata ca si rata anuala a dobanzii simple, suma finala ce urmeaza a fi restituita se calculeaza cu relatia:
Kf = K + n * K * rds = K(1+n*rds)
in care n - numarul de ani.
Dar sunt si situatii in care durata de acordare a creditului este exprimata in luni, trimestre sau decade.
In aceste conditii:
a) n = ![]() , daca durata este exprimata in luni;
, daca durata este exprimata in luni;
b) n = ![]() , daca durata este exprimata in trimestre;
, daca durata este exprimata in trimestre;
c) n = ![]() , daca durata este exprimata in decade.
, daca durata este exprimata in decade.
Revenind la relatia: Δd = ![]()
in mod logic se mai poate calcula:
a) volumul creditului:
K = ![]() ;
;
b) perioada de timp pentru care s-a acordat creditul:
t = ![]() ;
;
c) rata dobanzii simple:
rds
= ![]() .
.
Pentru creditor se pune problema evaluarii capitalului final (credit + dobanda) pe care il are de primit:
Kf = K+ Δd = K+![]() = K(1+
= K(1+![]() )
)
In care:
Kf valoarea capitalului final;
Δd volumul dobanzii.
In continuare pe baza ultimei relatii se pot calcula:
a) volumul creditului
K = 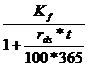
b) rata dobanzii simple:
rds = ![]()
Aplicatii
Problema nr. 1. O banca plaseaza un capital de 40.000.000 de lei intr-un credit pe o perioada de 240 de zile, la o rata a dobanzii simple anuale de 23%. Sa se calculeze valoarea dobanzii aferenta imprumutului si valoarea capitalului final.
Δd = ![]() =
= ![]() = 6.049.315 lei
= 6.049.315 lei
Kf = K+Δd = 40.000.000+6.049.315 = 46.049.315 lei
Problema nr. 2. Pe seama unui capital plasat intr-un credit pe o perioada de 180 de zile si cu o rata a dobanzii simple de 23% se va incasa o dobanda de 40.000.000 lei. Sa se calculeze valoarea creditului acordat si valoarea capitalului final.
K = ![]() =
= ![]() = 352.657.004,83 lei
= 352.657.004,83 lei
Kf = K+Δd = 352.657.004,83+40.000.000 = 392.657.004,83 lei
Calculul dobanzii simple cand rata dobanzii simple este variabila de la o perioada la alta
Relatia de calcul este:
Δd = K(rds1*t1+rds2*t2+rds3*t3+ +rdsn*tn)
sau:
Δd1 = K*rds1*t1
Δd2 = K*rds2*t2
Δd3 = K*rds3*t3
Δdn = K*rdsn*tn
Deci : Δd = Δd1+Δd2+Δd3+ +Δdn
In cazul in care duratele de timp sunt exprimate in zile, luni sau trimestre, valoarea capitalului initial se calculeaza cu relatia:
K = 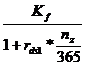 +
+ ++
++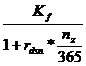
K =  +
+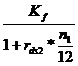 ++
++
K = 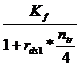 +
+ ++
++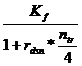
Rata dobanzii simple:
rds = ![]() +
+![]() +..+
+..+![]()
Respectiv:
rds = 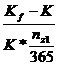 +
+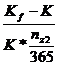 ++
++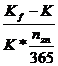
rds = 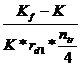 +
+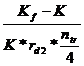 ++
++
Durata pentru care a fost acordat creditul:
n = rds = ![]() +
+![]() ++
++![]()
In fapt situatia se refera la cazul in care rata dobanzii simple capata valori diferite de la un an la altul, de la o perioada la alta:
Δd = Δd1+Δd2+Δd3+ +Δdn = K*rds1*n1+ K*rds2*n2++ K*rdsn*nn
Dar: n1 = n2 == nn = n
Δd = K*n(rds1+ rds2++ rdsn)
In situatiile in care duratele de timp sunt exprimate in zile, luni sau trimestre, relatiile de calcul devin:
a)
Δd
= K*rds1*![]() + K*rds2*
+ K*rds2*![]() +
+ K*rdsn*
+
+ K*rdsn*![]()
b)
Δd
= K*rds1*![]() + K*rds2*
+ K*rds2*![]() +
+ K*rdsn*
+
+ K*rdsn*![]()
c)
Δd
= K*rds1*![]() + K*rds2*
+ K*rds2*![]() +
+ K*rdsn*
+
+ K*rdsn*![]()
in care: nz numar de zile;
nl - numar de luni;
nt numar de trimestre.
Procedura de echivalenta in regim de dobanda simpla
Pentru o mai usoara asimilare propunem sa ne bazam pe un exemplu practic: O banca acorda un credit unui intreprinzator in valoare de 16.000 euro, rambursabil in urmatoarele conditii: prima rata de 4.000 de euro sa fie rambursabila dupa 30 de zile cu rds=9%, a doua rata de 5.000 de euro sa fie rambursata dupa 45 de zile cu rds=8%, iar a treia rata de 7.000 de euro sa fie rambursata dupa 80 de zile cu rds=14%.
Volumul total al dobanzii va fi de:
Δd = Δd1+Δd2+Δd3 = K1*rds1*t1+ K2*rds2*t2+ +K3*rds3*t3 =
=4000*0.09*![]() +5000*0.08*
+5000*0.08*![]() +7000*0.14*
+7000*0.14*![]() = 29,58+8,88+214,79 = 253,25
= 29,58+8,88+214,79 = 253,25
Fata de aceste conditii initiale, creditorul si intreprinzatorul, de comun acord accepta intre timp ca imprumutul si dobanda sa fie restituita la un anumit termen (o singura data) diferit fata de termenele intermediare prestabilite si care sa nu conduca la modificarea volumului dobanzii. In acest caz avem de-a face cu o procedura de echivalenta in regim de dobanda simpla. In aceasta situatie este evident ca:
t1 = t2 = t3 == t
Si intrucat cunoastem volumul dobanzii se va obtine:
Δd = K1*rds1*t1+ K2*rds2*t+ K3*rds3*t3 = t(K1*rds1+ K2*rds2+ K3*rds3)
253,25 = t(4000*0,09+5000*0,08+7000*0,14) = 1740*t
De unde rezulta :
t = ![]() = 0,145 ani = 53,10
zile
= 0,145 ani = 53,10
zile
In acest tip de produs i echivalenta in regim de dobanda simpla ne putem confrunta cu urmatoarele tipuri de situatii:
a) rds sa fie egale pentru fiecare interval de timp;
b) ratele de credit sa fie egale.
a) Δd = K1*rds1*t1+ K2*rds2*t+ K3*rds3*t3
253,25 = 4000* rds1*![]() +5000* rds2*
+5000* rds2*![]() +7000* rds3*
+7000* rds3*![]()
Deoarece: rds1 = rds2 = rds3 = rds relatia devine :
253,25 = rds(4000*![]() +5000*
+5000*![]() +7000*
+7000*![]() ) = 2479,42* rds
) = 2479,42* rds
rds = ![]() = 0,102 = 10,2%
= 0,102 = 10,2%
Putem verifica daca volumul dobanzii se modifica daca rds este de 10,2% pentru toate intervalele de timp:
Δd = 4000*0,102*![]() +5000*0,102*
+5000*0,102*![]() +7000*0,102*
+7000*0,102*![]() =
=
=33,5+62,8+156,49 = 252,89![]() 253,12
253,12
b) Δd = K1*rds1*t1+ K2*rds2*t+ K3*rds3*t3
K1 = K2 = K3 = K relatia devine :
Δd = K(0,09*![]() +0,08*
+0,08*![]() +0,14*
+0,14*![]() )
)
253,12 = K(0,0073+0,098+0,0306) = 0,0477*K
K = ![]() = 5309,22
= 5309,22
Procedura financiara multipla in regim de dobanda simpla
In activitatea practica se pot intalni situatii in care creditorul acorda intreprinzatorului mai multe credite (K1, K2, K3, Kn) cu rate ale dobanzii aferente fiecarui credit, diferite (rds1,rds2,rds3,rdsn) pe perioade diferite (t1, t2, t3, tn). Se considera ca doua proceduri financiare multiple in regim de dobanda simpla devin echivalente daca volumul dobanzilor este acelasi Δd1 = Δd2.
![]()
![]() Se urmareste, daca exista interes reciproc
de a inlocui procedura P1 cu procedura P2 si daca
variabilele procedurii P2 pot inlocui variabilele procedurii P1,
cu alte cuvinte sunt substituibile. Sa propunem ca exista urmatoarea
procedura multipla care este exprimata in forma matriceala:
Se urmareste, daca exista interes reciproc
de a inlocui procedura P1 cu procedura P2 si daca
variabilele procedurii P2 pot inlocui variabilele procedurii P1,
cu alte cuvinte sunt substituibile. Sa propunem ca exista urmatoarea
procedura multipla care este exprimata in forma matriceala:
P1 =![]()
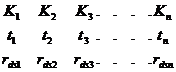
Sunt doua situatii care prezinta interes in activitatea practica:
A) sa vedem daca procedura financiara multipla P1, prezentata anterior in forma matriceala, poate fi inlocuita cu alta procedura matriceala P2, dar in care, pe rand, elementele de pe orizontala sunt egale intre ele (K, t si rds):
a) K1 = K2 = K3 == Kn = K;
b) t1 = t2 = t3 == tn = t ;
c) rds1 = rds2 = rds3 = = rdsn = rds.
Volumul total al dobanzii:
Δd = K1*rds1*t1+ K2*rds2*t+ + Kn*rdsn*tn
a) Volumul total al dobanzii se calculeaza astfel :
Δd = K1*rds1*t1+ K2*rds2*t+ + Kn*rdsn*tn
Procedurile P1 si P2 devin echivalente daca volumul dobanzii aferent fiecarei proceduri sunt egale:
Δd1 = Δd2
Δd1 = K1*rds1*t1+ K2*rds2*t2+ + Kn*rdsn*tn
Δd2 = K1*rds1*t1+ K2*rds2*t2+ + Kn*rdsn*tn
Dar : K1 = K2 = K3 == Kn = K
De unde se poate calcula valoarea lui K:
K1*rds1*t1+ K2*rds2*t+ + Kn*rdsn*tn = K*rds1*t1+ K*rds2*t+ + K*rdsn*tn=
=K(rds1*t1+rds2*t+ +rdsn*tn)
K = ![]()
b) In aceasta situatie se presupune ca in procedura P1 se inlocuieste procedura multipla matriceala P3 de forma:
t1 = t2 = t3 == tn =t
![]()
![]()
P3 = 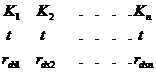
![]()
Atunci: Δd3 = K1*rds1*t+ K2*rds2*t+ + Kn*rdsn*t
Δd1 = Δd3
K1*rds1*t1+ K2*rds2*t2+ + Kn*rdsn*t3 = K1*rds1*t+ K2*rds2*t+ + Kn*rdsn*t=
= t(K1*rds1+ K2*rds2+ + Kn*rdsn)
De unde se poate calcula valoarea necunoscuta a lui t0:
t = ![]()
c) Sa presupunem ca procedura P1 va fi inlocuita de o procedura matriceala multipla P4 de forma:
rds1 = rds2 = rds3 = = rdsn = rds
![]()
![]()
P4 = 
Δd4 = K1*rds*t1+ K2*rds*t2+ + Kn*rds*tn
Δd1 = Δd4
K1*rds1*t1+ K2*rds2*t2+ + Kn*rdsn*t3 = K1*rds1*t+ K2*rds2*t+ + Kn*rdsn*t=
= rds(K1*t1+ K2*t2+ + Kn*tn)
Deci se poate calcula valoarea necunoscuta a ratei dobanzii simple:
rds = ![]()
Daca pentru o suma initiala/credit K depusa sau creditat, volumul dobanzii se modifica periodic iar valoarea corespunzatoare pentru un interval de timp devine valoarea initiala pentru urmatorul interval de timp si se aplica procedeul de dobanda la dobanda avem de-a face cu ceea ce se numeste dobanda compusa. Pentru primul interval de timp volumul dobanzii (Δd) va fi Δd1 = K*rd1. Pentru al doilea interval de timp: Δd2 = K+ Δd1 s.a.m.d.
Dobanda aferenta unui credit care nu e restituita la momentul de timp stabilit de comun acord, se va acumula cu creditul imprumutat, care va genera o noua dobanda (dobanda la dobanda) iar suma corespunzatoare devine suma initiala pentru urmatorul interval de timp. Cu alte cuvinte, capitalul initial (K) se modifica periodic prin capitalizarea dobanzii calculate pentru perioada anterioara.
Pentru generalizare vom concepe urmatorul tabel:
|
An |
Suma initiala (K) |
Δds |
Suma finala (Kf) |
|
K |
K* rds |
K+ rds*K= K(1+rds) |
|
|
K(1+rds) |
K(1+rds)* rds |
K(1+rds)+ K(1+rds)* rds=K(1+rds) (1+rds)=K(1+rds)2 |
|
|
n |
K(1+rds)n-1 |
K(1+rds)n-1*rds |
K(1+rds)n |
Deci la sfarsitul celor n ani capitalul final va fi:
Kf = K(1+rds)n
Valoarea dobanzii Δd = Kf-K = K(1+rds)n-K = K[(1+rds)n-1]
Se poate calcula valoarea prezenta sau actualizata:
K = ![]()
Kf = K(1+rds)n
![]() = (1+rds)n
= (1+rds)n
Apoi: ln![]() = ln(1+rds)n relatie care nu
permite sa calculam numarul de ani pentru
= ln(1+rds)n relatie care nu
permite sa calculam numarul de ani pentru
care s-a acordat creditul:
n = 
In aceste conditii putem calcula si rds:
![]() = n*
= n* ![]()
![]() =
= ![]()
![]() = e
= e![]()
![]() = e
= e![]() = (
= (![]() )
)![]()
rs = (![]() )
)![]() -1 =
-1 = ![]() -1
-1
Volumul dobanzii se calculeaza astfel:
Δd = Kf-K=K[(1+rds1)+ (1+rds2)+ + (1+rdsn)]-K=K[(1+rds1)+ (1+rds2)+ + (1+rdsn)-1]
Presupunand ca: rds1 = rds2 = rds3 = = rdsn =rds
Kf = K(1+rds)n
Intrucat este vorba de rata dobanzii compuse se aplica principiul dobanda la dobanda rds va fi numita rdc, rata dobanzii compuse.
3.1. Rata dobanzii compuse variabile
Aidoma situatiei de la rata dobanzii simple si in acest caz se pleaca de la ideea ca si rata dobanzii compuse poate avea valori diferite pe parcursul anumitor intervale de timp.
Ramane valabila constatarea ca pentru intervalul de timp urmator, valoarea initiala (suma credit) este valoarea finala (suma credit) a anului anterior.
Problema nr.3. O suma de 5000 de euro e depusa la o banca pe o perioada de 3 ani cu o rata a dobanzii de 7% pentru primul an, 9% pentru cel de-al doilea an si 11% pentru cel de-al treilea an.
Pentru primul an:
Δd1 = K*rd1 = 5000*0,07 = 350
K1 = K+ Δd1 = 5000+350 = 5350
Sau: K1 = K(1+ rds1) = 5000*1,07 = 5350
Sau: Δd1 = K1-K = 5350-5000 =350
Pentru al doilea an:
Δd2 = K(1+*rds1)*rd2 = 53500*0.09 = 481,5
K2 = K1+ Δd2 =K(1+ rds1)+K(1+ rds2)(1+rd2)=K(1+rds1) (1+rds2)=5350+481,5=5831,5
Δd2 = K2- K1 = K(1+ rds1)(1+rds2)- K(1+ rds1) = K(1+ rds1)[ (1+ rds2)-1] = 481,5
Pentru al treilea an:
Δd3 = K(1+ rds1) (1+ rds2)* rds3 = 641,46
K3 = K2+ Δd3 = K(1+ rds1) (1+ rds2) (1+ rds3) = 6472,96
Δd3 = K3-K2 = K(1+ rds1)(1+ rds2)(1+ rds3)-K(1+rds1)(1+rds2) = K(1+rds1) (1+rds2)*
*[(1+rds3)-1] = 641,46
In forma generala suma finala (credit, valoare) se calculeaza cu relatia:
Kf = K(1+ rds1) (1+ rds2) (1+ rds3)* * (1+ rdsn)
Iar volumul dobanzii:
Δd3 = Kf-K = K(1+ rds1) (1+ rds2) (1+ rds3)* * (1+ rdsn)-K =
= K[(1+ rds1) (1+ rds2) (1+ rds3)* * (1+ rdsn)-1] =
= K[(1+ rds1) (1+ rds2) (1+ rds3)* * (1+ rdsn-1)]*rdsn
|
Politica de confidentialitate |
| Copyright ©
2026 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |