
UNIVERSITATEA DIN ORADEA
FACULTATEA DE STIINTE ECONOMICE
SPECIALIZAREA
Modelul econometric pentru
creditele in euro
in functie de rata dobanzii
Introducere
CREDITELE IN EURO
"Creditul reprezinta relatia baneasca intre o persoana fizica sau juridica, numita creditor, care acorda unei alte persoane, numita debitor, un imprumut in bani in general cu o dobanda stabilita in functie de riscul pe care si-l asuma creditorul sau de reputatia debitorului". Etimologic, cuvantul "credit" isi are originea in limba latina "creditum-creditare", care inseamna "a crede" sau "a avea incredere", fapt ce scoate la iveala un element de ordin psihologic: increderea, care presupune existenta unei anumite culturi sociale, a unei "psihologii colective", care difera insa in timp si de la o colectivitate la alta.
Creditul in euro reprezinta aceea suma valorica in moneda euro, acordata pe termen scurt mediu sau lung unei persoane care prezinta o nevoie de finantare.
RATA DOBANZII LA CREDITELE IN EURO
Rata dobanzii de politica monetara a creditelor in euro este
rata la care BNR atrage depozite pe termen de o saptamana de pe
piata monetara interbancara.
-Nivelul ratelor dobanzilor aferente facilitatilor permanente
acordate de catre BNR (facilitatea de depozit si facilitatea de
credit) se inscriu, intr-un coridor simetric de +/-4 puncte procentuale
fata de rata dobanzii de politica monetara. marti, pe
langa majorarea dobanzii de politica monetara, si cresterea
dobanzii pentru facilitatea de depozit, cu 3,75
puncte procentuale, la 5,75% pe an, si a dobanzii pentru facilitatea de credit
(Lombard) de la 12%, la 13,75% pe an.In acelasi timp, banca
centrala a decis reducerea scadentei pentru operatiunile de
atragere de depozite de la doua saptamani la o
saptamana, masura care va intra in vigoare la data
derularii urmatoarei licitatii pentru operatiuni de acest
tip, se arata intr-un comunicat al BNR.Analizand ofertele bancilor
existente pe piata romaneasca, reiese ca creditele contractate in euro sunt mai
avantajoase decat cele contractate in lei, conchide siteul financiar FinZoom.
Si asta pentru ca la comisioane comparabile dobanzile pentru creditele acordate
in moneda europeana sunt mult mai scazute decat dobanzile aferente creditelor
in lei. La randul lor, dobanzile anuale efective (DAE) oferite de creditele in
euro sunt mai mici decat DAE pentru creditele ipotecare in lei, chiar si cu 2,6
puncte procentuale.
Tendintele
arata ca din ce in ce mai multi romani apeleaza la creditele in euro pentru
nevoile proprii de finantare. Si asta pentru ca, in cazul in care dispuneti de
un avans, creditul ipotecar sau imobiliar oferit de banci este in continuare
cea mai buna metoda de finantare a unei investitii imobiliare, potrivit
aprecierilor analistilor site-urilor financiare.
Potrivit Ziarului financiar, odata ridicata aceasta restrictie, practic a
disparut bariera despartitoare dintre creditul in euro si creditul in lei, in
cazul caruia nu se solicita avans, insa costurile sunt mult mai ridicate. Cei
interesati in a contracta in perioada imediat urmatoare un credit cu siguranta
isi vor pune problema monedei in care va fi incheiat contractul de credit,
pentru ca, in functie de aceasta, difera si rata dobanzii, comisioanele, precum
si durata si suma maxima ce poate fi obtinuta
Oferta bancilor romanesti este cat de cat asemanatoare atat in ceea ce priveste
creditele contractate in lei, cat si in
privinta celor contractate in euro.
Dispunem de 36 observatii asupra marimii lui y si x.
|
luna |
yt |
xt |
|
creditul |
ratele dobanzii |
|
|
2005ian | ||
|
Feb | ||
|
Mar | ||
|
Apr | ||
|
Mai | ||
|
Iun | ||
|
Iul | ||
|
Aug | ||
|
Sept | ||
|
Oct | ||
|
Noi | ||
|
Dec | ||
|
2006ian | ||
|
Feb | ||
|
Mar | ||
|
Apr | ||
|
Mai | ||
|
Iun | ||
|
Iul | ||
|
Aug | ||
|
sept | ||
|
Oct | ||
|
Noi | ||
|
Dec | ||
|
2007ian | ||
|
Feb | ||
|
Mar | ||
|
apr | ||
|
Mai | ||
|
Iun | ||
|
Iul | ||
|
Aug | ||
|
Sept | ||
|
Oct | ||
|
Noi | ||
|
Dec |
Reprezentam grafic norul de puncte:
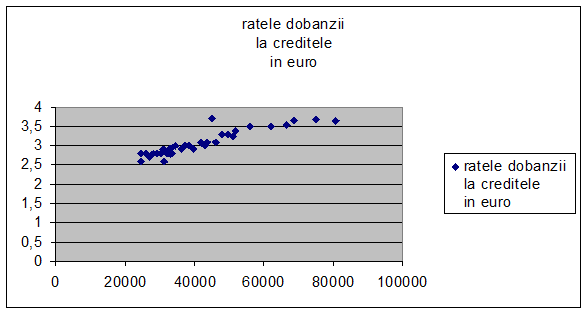
Cometarii privind aspectul norului de puncte.
Privind desenul observam ca punctele sunt grupate , deci intre x si y exista legatura.
Daca punctele sunt grupate in jurul unei drepte intre x si y exista o legatura liniara .
In ceea ce priveste intensitatea cu cat punctele sunt grupate mai mult in jurul liniei imaginare cu atat legatura este mai puternica.
Sensul legaturii poate fi directa ascedenta sau indirecta descedenta in cazul meu este este o legatura directa , deci ascendenta . Parametrul a<0 , Ry/x <0 .
Pentru analiza creditului in euro am ales urmatorul model:
![]()
unde:
yt = creditul in euro din luna t
xt = rata dobanzii la creditele in euro in luna t
εt = variabila reziduala
Ecuatia (1) se poate scrie sub forma matriciala:
![]()
cu 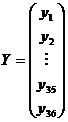 ,
, 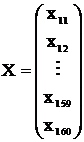
Am notat:
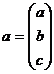
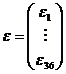
1. Ipoteze fundamentale
(i) xt si yt reprezinta valori numerice ale variabilelor X si Y rezultate prin observarea statistica, neafectate de erori sistematice;
(ii) Y este variabila endogena aleatoare, pentru ca este functie de
(iii) X, variabila explicativa, este considerata ca fiind o variabila determinista in model, nealeatoare;
(i) ε are o distributie independenta de timp, de speranta matematica nula, respectiv:
E (εt) = 0, ( ) t = 0, 1, 2, ., T
V (εt)
= E[εt -
E(εt)]2 = ![]() =
= ![]()
altfel spus, modelul este homoscedastic.
(ii) Independenta erorilor. Doua erori εt si εt' sunt independente liniar intre ele, adica
![]()
respectiv
![]()
(iii) Variabila ε are o distributie normala.
(i)
cov(xt, εt)
= 0, ![]() t - erorile
sunt independente de X;
t - erorile
sunt independente de X;
(ii) Se presupune ca pentru T , primele doua momente empirice ale variabilei X sunt finite, respectiv
Speranta matematica
![]()
Varianta ![]()
2. Determinarea estimatorilor de regresie liniara prin metoda celor mai mici patrate
Aplicam metoda celor mai mici patrate pentru determinarea coeficientilor.
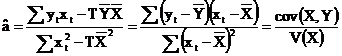 =0.91
=0.91
![]() = -82494.97
= -82494.97
Deci modelul intre creditul in euro si ratele dobanzii la creditele in euro este:
Y=0.91*X-82494.97
3. Testarea validitatii modelului
Testarea validitatii modelului presupune parcurgerea urmatoarelor etape:
Testarea validitatii modelului de regresie folosind metoda descompunerii variantei;
Calculul raportului de corelatie si testarea semnificatiei lui;
Inferenta statistica pentru parametrii modelului de regresie;
Verificarea ipotezelor modelului de regresie.
Testarea validitatii modelului de regresie folosind metoda descompunerii variantei
Dispersia totala verifica urmatoarea relatie:
![]()
Termenii relatiei se definesc prin:
![]() - varianta
totala a variabilei Y determinata de toti factorii
sai de influenta;
- varianta
totala a variabilei Y determinata de toti factorii
sai de influenta;
![]() - varianta
fenomenului Y determinata
numai de variatia factorului X,
considerat factorul principal al variabilei Y, adica variatia lui Y explicata de modelul
econometric;
- varianta
fenomenului Y determinata
numai de variatia factorului X,
considerat factorul principal al variabilei Y, adica variatia lui Y explicata de modelul
econometric;
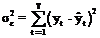 - variatia
reziduala, sau variatia fenomenului Y generata de catre factorii nespecificati in
model, acesti factori fiind considerati - in etapa de specificare -
drept factori cu influenta intamplatoare, neesentiali
pentru a explica variatia fenomenului Y
- variatia
reziduala, sau variatia fenomenului Y generata de catre factorii nespecificati in
model, acesti factori fiind considerati - in etapa de specificare -
drept factori cu influenta intamplatoare, neesentiali
pentru a explica variatia fenomenului Y
Descompunerea variantei - Metoda ANOVA
|
Sursa de variatie |
Masura variatiei |
Numarul gr. de libertate |
Dispersii corectate |
Valoarea testului F |
|
|
Fcalc |
Fα;v1;v2 |
||||
|
Varianta explicata de model, datorata factorului X |
|
k = 1 |
|
| |
|
Varianta Reziduala, datorata factorilor neesentiali |
|
T - k - 1 |
| ||
|
Varianta totala |
|
T - 1 |
| ||
Pe baza datelor din tabel se pot testa urmatoarele ipoteze:
H : s2Y/X s2 , cele doua dispersii sunt aproximativ egale, influenta factorului X nu difera semnificativ de influenta factorilor intamplatori.
H : s2Y/X s2 , influenta factorului X si a factorilor intamplatori - masurata prin cele doua dispersii - difera semnificativ si, deci, se poate trece la discutia similitudinii, a verosimilitatii modelului teoretic in raport cu modelul real.
Acceptarea ipotezei H0 este echivalenta cu respingerea modelului (modelul nu este valid).
Testarea semnificatiei dintre doua dispersii se face cu ajutorul distributiei teoretice Fisher-Snedecor, respectiv cu testul F.
Cunoscand cele doua valori, ![]() = , si Fα,v1,v2= 4.17 .valoarea
teoretica a variabilei F,
preluata din tabelul repartitiei Fisher - Snedecor, in functie
de un prag de semnificatie α si un numarul gradelor de
libertate = k; = n-k-1, regula de decizie se
scrie:
= , si Fα,v1,v2= 4.17 .valoarea
teoretica a variabilei F,
preluata din tabelul repartitiei Fisher - Snedecor, in functie
de un prag de semnificatie α si un numarul gradelor de
libertate = k; = n-k-1, regula de decizie se
scrie:
- se accepta H0 si se respinge H1 daca Fcalc ≤ Fα, deci modelul nu este valid;
- se accepta H1 si se respinge H0 daca Fcalc >Fα, , deci modelul este valid.
3.2. Calcularea coeficientului de corelatie R2, a coeficientului de corelatie corectat si testarea reprezentativitatii lui
Coeficientul de corelatie R2 exprima rolul jucat de ansamblul variabilelor exogene asupra variabilei endogene. Cu cat valoarea acestuia este mai apropiata de 1, cu atat legatura dintre variabile este mai intensa.
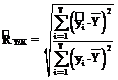
Efectuam calculele si obtinem:
![]()
In cazul acesta avem o intensitate medie spre puternica,pragul maxim fiind de 1. Legatura este directa, deci cresterea Cursului de schimb determina cresterea valorii Exportului.
Testarea
reprezentativitatii lui ![]()
H0:
![]() = 0
= 0
H1:
![]() ≠ 0
≠ 0
![]() 183
183
Se compara valoarea calculata a lui F cu cea tabelara. Regulile de decizie sunt urmatoarele:
- daca Fcalc < Ftab, ipoteza nula este cea care este acceptata, fapt echivalent cu inexistenta unei legaturi intre cele doua variabile la nivel de populatiei totala.
- daca Fcalc > Ftab, ipoteza nula este cea care se respinge, acceptandu-se cea alternativa.
Intrucat
Fcalc>Ftab rezulta ca dintre cele doua
ipoteze cea de-a doua este adevarata H1: ![]() ≠ 0, comparand
cele doua se confirma ca legatura este de intensitate medie spre puternica la
nivelul intregii populatii.
≠ 0, comparand
cele doua se confirma ca legatura este de intensitate medie spre puternica la
nivelul intregii populatii.
3.3. Teste si regiuni de incredere
3.3.1.Testarea validitatii estimatiei coeficientilor
Pentru testarea validitatii estimatiei coeficientilor ai se utilizeaza testul Student. In general :
H0 : ai = 0, cu alternativa
H1 : ai ≠ 0
Daca 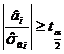 atunci H0
se respinge, iar coeficientul ai este semnificativ diferit de 0.
atunci H0
se respinge, iar coeficientul ai este semnificativ diferit de 0.
Pentru parametrul a emitem ipotezele:
H0 : a = 0, cu alternativa
H1 : a ≠ 0
Dupa efectuarea calculelor, obtinem:
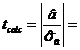 13.53653
13.53653
si stim ca ttab = 1.96
Comparam cele doua valori si tragem concluzia ca ipoteza adevarata este H1 cu o probabilitate de 95%, ceea ce inseamna ca a este diferit de 0.
Idem pt. parametrul b.
Pentru parametrul b emitem ipotezele:
H0 : b = 0, cu alternativa
H1 : b ≠ 0
Dupa efectuarea calculelor, obtinem:
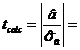 -8.945653
-8.945653
si stim ca ttab = 1,96
Comparam cele doua valori si tragem concluzia ca ipoteza adevarata este H1 cu o probabilitate de 95%, ceea ce inseamna ca b este diferit de 0.
3.3.2. Intervale de incredere pentru coeficienti
Acestea se stabilesc cu un prag de semnificatie α = 0,05.
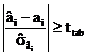 deci
deci ![]()
Dupa efectuarea calculelor obtinem urmatoarele intervale de incredere, cu o probabilitate de 95%:
-0.74061≤a≤0.977847
-88370.46≤b≤-79497.314
3.4. Testarea ipotezelor fundamentale referitoare la variabila aleatoare ε
. Ipoteza de homoscedasticitate a variabilei reziduale - Testul White
Testul White - etape:
- estimarea parametrilor modelului initial si calculul valorilor estimate ale variabilei reziduale, εt
- construirea unei regresii auxiliare, bazata pe prespunerea existentei unei relatii de dependenta intre patratul valorilor erorii, variabila exogena inclusa in modelul initial si patratul valorilor acesteia:
![]()
- calcularea coeficientului de corelatie estimat, corespunzator acestei regresii auxiliare
- testarea semnificatiei raportului de corelatie. Daca acesta este semnificativ diferit de zero, atunci ipoteza de heteroscedasticitate a erorilor este acceptata.
![]()
![]()
LMcalc = TR2
LM=36*0.83=13.68
![]()
Daca LMcalc > (k grade de libertate, k - numarul de variabile exogene) , erorile sunt heteroscedastice, in caz contrar, sunt homoscedastice.
VAL TAB=0.4
Erorile sunt heteroscedastice, deci modelul nu este valid. El nu poate fi folosit pentru previziuni statistice.
3.4.2. Ipoteza independentei valorilor variabilei reziduale εt
Aceasta ipoteza presupune verificarea relatiei:
![]()
Depistarea autocorelarii erorilor se poate face utilizand Testul Durbin - Watson. Functia de autocorelatie descrie intensitatea analogiei dintre doi termeni yt si yt-k .In ceea ce priveste autocorelarea valorilor variabilei reziduale, a fost elaborat in 1950, de catre Durbin J. si Watson G. S. un test intens utilizat si in prezent. Se obtine:
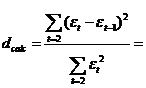 1.703234
1.703234
Valoarea empirica, dcalc, se compara cu doua valori teoretice, d1 si d2, citite din tabelul distributiei Durbin - Watson in functie de un prag de semnificatie , convenabil ales, ( = 0,05 sau = 0,01), de numarul de variabile exogene, k si de valorile observate T, T
Regulile de decizie a testului sunt:
d1=1.49
d2=1.52
|
< DWcalc < d1 |
d1 DWcalc d2 |
d2 < DWcalc < 4 - d2 |
4 - d2 DWcalc 4 - d1 |
4 - d1 < DWcalc < 4 |
|
Autocorelare pozitiva |
Indecizie |
Erorile sunt independente |
Indecizie |
Autocorelare negativa |
Deoarece dcal este cuprins intre 0si d1 rezulta ca intre erori exista o autocorelatie pozitiva,nici aceasta ipoteza nu este verificata datorita faptului ca dcalc nu apartine coloanei a treia care ar fi validat modelul.Din nou modelul nu este valid
z
3.4.2.Testarea normalitatii distributiei variabilei aleatoare ε
O modalitate de verificare a ipotezei de normalitate a erorilor o constituie testul Jarque - Berra, care estel un test asimptotic, valabil in cazul unui esantion de volum mare, ce urmeaza o distributie hipatrat cu cu 2 grade de libertate, avand urmatoarea forma:
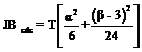 =15.95331
=15.95331
unde:
n - numarul de observatii;
coeficientul de asimetrie (skewness), ce masoara simetria distributiei erorilor in jurul mediei acestora (medie care este nula), avand urmatoarea relatie de calcul:
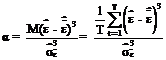 =1.162
=1.162
β - coeficientul de boltire al lui Pearson (kurtosis), ce masoara boltirea distributiei in raport cu distributia normala, ce are urmatoarea relatie de calcul:
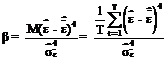 =0.713
=0.713
Testul Jarque - Berra se bazeaza pe ipoteza ca distributia normala are un coeficient de asimetrie egal cu zero, = 0, si un coeficient de aplatizare egal cu trei, β = 3.
Daca ![]() , atunci ipoteza de normalitate a erorilor este
respinsa.
, atunci ipoteza de normalitate a erorilor este
respinsa.
4. Previziunea variabilei y
Pentru luna mai 2008, pentru variabila x s-a previzionat o valoare de 3.7. in aceasta situatie variabila y creditul, previzionata va inregistra urmatoarele valori:
I. Previziune punctuala yp=67644.6
II. Previziune prin interval de incredere: 63271.1≤yp≤72018.2
|
Politica de confidentialitate |
| Copyright ©
2026 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |