
I. Introducere
In prima parte a proiectului am analizat legatura dintre variabila dependenta (PIB-ul Frantei, exprimat in miliarde euro) si variabila independenta (importuri), intre anii 1960-1980. Apoi, cu ajutorul programului Microsoft EXCEL am realizat calculele pe care le-am interpretat, in timp ce calculele propriu-zise sunt localizate in anexe.
Cea de-a 2 a parte a proiectului o reprezinta regresia bifactoriala. Aici, am adaugat inca o variabila independenta (si anume exporturile), din aceeasi perioada.
II. Descrierea variabilelor regresiei unifactoriale
In urmatorul tabel avem date referitoare la PIB-ul Frantei (reprezentand variabila dependenta y), cat si informatii despre importuri (fiind insusite variabilei independente x). Valorile sunt exprimate in miliarde euro, iar perioada studiului este 1960-1980.
|
An |
PIB (y |
Importuri (x |
Sursa datelor prezentate mai sus este: Conturile Nationale - Baza 2000 (Institutul National de Statistica al Frantei)
Cu ajutorul datelor din tabelul de mai sus, vom putea construi un model liniar factorial de forma: y = f (x) +
y = valorile variabilelor dependente;
x = valorile variabilelor independente;
ε = variabila reziduala, reprezentand influentele celorlalti factori ai variabilei y.
Pasul urmator este alegerea unei functii f(x) pe baza careia sa determinam legatura dintre variabile. Construirea unei astfel de legaturi se face prin intocmirea corelogramei (fig. 1)
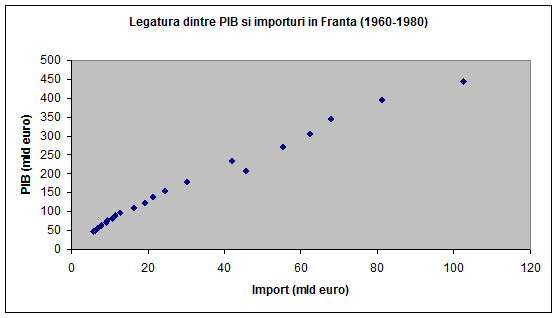
fig. 1
Din corelograma deducem ca distributia punctelor xi si yi poate fi aproximata cu o dreapta, asadar legatura dintre variabile reprezinta un model liniar unifactorial de forma:
y = a + bx + u
a,b - parametrii modelului;
b![]() 0 - (panta
dreptei) deoarece legatura dintre cele doua variabile este
directa.
0 - (panta
dreptei) deoarece legatura dintre cele doua variabile este
directa.
Legatura ce demonstreaza ca modelul econometric este unul liniar unifactorial este redata in figura urmatoare (fig. 2).
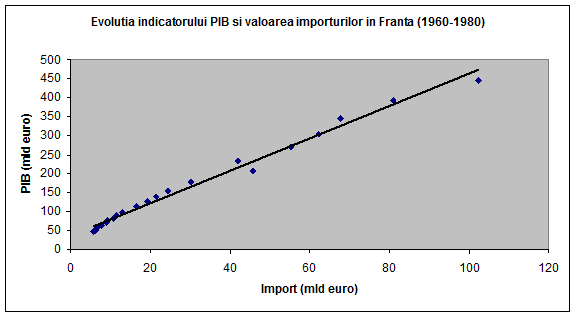
fig. 2
III. Calculul problemei in EXCEL
|
SUMMARY OUTPUT |
|
|
Regression Statistics |
|
|
Multiple R | |
|
| |
|
Adjusted | |
|
Standard Error | |
|
Observations | |
|
ANOVA |
|||||
|
df |
SS |
MS |
F |
Significance F |
|
|
Regression |
6.46519E-20 |
||||
|
Residual | |||||
|
Total | |||||
|
Coefficients |
Standard Error |
t Stat |
P-value |
Lower 95% |
Upper 95% |
|
|
Intercept |
5.76714E-08 | |||||
|
X Variable1 |
6.46519E-20 |
|
RESIDUAL OUTPUT |
||
|
Observation |
Predicted Y |
Residuals |
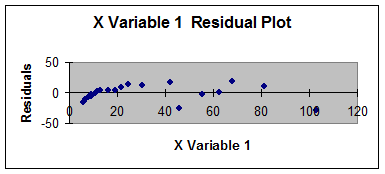
Interpretari ale rezultatelor obtinute:
Tabelul SUMMARY OUTPUT
R = 0.9942 denota faptul ca intre PIB si import exista o legatura stransa in economia Frantei
R2 0.9885 arata ca 98% din variatia PIB-ului se datoreaza importurilor masive din Franta
Abaterea medie patratica a erorilor ![]() 13.1896 reprezinta
abaterea punctelor fata de dreapta de regresie. Valoarea acestui indicator
demonstreaza ca functia de regresie este reprezentativa.
13.1896 reprezinta
abaterea punctelor fata de dreapta de regresie. Valoarea acestui indicator
demonstreaza ca functia de regresie este reprezentativa.
Numarul de observatii: 21
Pentru aceasta problema putem afirma ca modelul de regresie liniara simpla este bun.
Tabelul ANOVA
Acest tabel se refera la descompunerea variantei totale (SST), variabila dependenta in doua componente: varianta explicata prin regresie (SSR) si varianta reziduala (SSU).
El este compus din, suma patratelor (SS), numarul gradelor de libertate (df), media patratica (MS), raportul ANOVA (F), si pragul de semnificatie (Signigicance F).
Rezultatele
din acest tabel sunt folosite pentru construirea testului F. Totodata, datele furnizate
de analiza dispersionala (ANOVA), pot valida sau invalida modelul de regresie
construit. Astfel, intrucat F = 1643.2787
si Significance F (pragul de semnificatie) = 6.4651 ![]() , valoare care
este mai mica decat 0.05, confirma ca modelul este valid deci poate fi utilizat
pentru analiza dependentei dintre PIB si Importuri in cadrul economiei franceze
din perioada 1960-1980.
, valoare care
este mai mica decat 0.05, confirma ca modelul este valid deci poate fi utilizat
pentru analiza dependentei dintre PIB si Importuri in cadrul economiei franceze
din perioada 1960-1980.
Al doilea tabel al analizei ANOVA, reda valorile coeficientilor modelului de regresie (Coefficients), erorile standard ale coeficientilor (Standard Error), dar si informatii pentru aplicarea testului Student pentru fiecare coeficient (t-stat si P-value). Valorile coloanei t-stat se obtin prin impartirea coeficientilor la erorile standard care le corespund, asadar obtinem valorea calculata a testului t pentru fiecare estimator (coeficient). Dupa cum se obisnuieste, aceastea valoare se compara cu cea tabelara din repartitia Student.
Intercept
reprezinta termenul liber al functiei, asadar ![]() = 37.1899
Acest punct reprezinta locul in care variabila factoriala este 0, adica volumul
PIB-ului in miliarde euro in cazul in care importurile tind spre 0. Intrucat
= 37.1899
Acest punct reprezinta locul in care variabila factoriala este 0, adica volumul
PIB-ului in miliarde euro in cazul in care importurile tind spre 0. Intrucat ![]() = si
pragul de semnificatie P-value = 5.7671
= si
pragul de semnificatie P-value = 5.7671 ![]() valoare mai mica decat
0.05, putem afirma ca coeficientul este semnificativ. Intervalul de incredere
al acestui parametru este 28.1248
valoare mai mica decat
0.05, putem afirma ca coeficientul este semnificativ. Intervalul de incredere
al acestui parametru este 28.1248 ![]()
![]()
![]() 46.2550
46.2550
Pe de alta parte, ![]() = 4.2536 astfel la cresterea
importurilor cu un miliard de euro, PIB-ul Frantei va creste cu 4.2536 miliarde
euro. Aplicand acelasi rationament ca la
= 4.2536 astfel la cresterea
importurilor cu un miliard de euro, PIB-ul Frantei va creste cu 4.2536 miliarde
euro. Aplicand acelasi rationament ca la ![]() ,
,
![]() = 40.5373 si P-value este 6.4651
= 40.5373 si P-value este 6.4651 ![]() care este mai mica
decat 0.05, deci coeficientul este semnificativ. Intervalul de incredere pentru
care este mai mica
decat 0.05, deci coeficientul este semnificativ. Intervalul de incredere pentru
![]() este 4.0340
este 4.0340![]()
![]()
![]() 4.4733.
4.4733.
IV. Regresie bifactoriala - legatura dintre PIB si importuri si exporturi, in economia Frantei din perioada 1960-1980.
Regresia bifactorialǎ
Daca in prima parte a proiectului, am utilizat ca variabila independenta doar importurile, in ce-a de-a 2 a parte, voi adauga si exporturile in regresie. Perioada este aceeasi.
|
An |
PIB (Y) |
Importuri (X1) |
Exporturi (X2) |
|
| |||
Sursa datelor prezentate mai sus este: Conturile Nationale - Baza 2000 (Institutul National de Statistica al Frantei)
|
SUMMARY OUTPUT |
|
|
Regression Statistics |
|
|
Multiple R | |
|
| |
|
Adjusted | |
|
Standard Error | |
|
Observations | |
|
ANOVA |
|||||
|
df |
SS |
MS |
F |
Significance F |
|
|
Regression |
4.0246E-22 |
||||
|
Residual | |||||
|
Total | |||||
|
Coefficients |
Standard Error |
t Stat |
P-value |
Lower 95% |
Upper 95% |
|
|
Intercept | ||||||
|
X Variable1 | ||||||
|
X Variable2 |
|
RESIDUAL OUTPUT | ||
|
Observation |
Predicted Y |
Residuals |
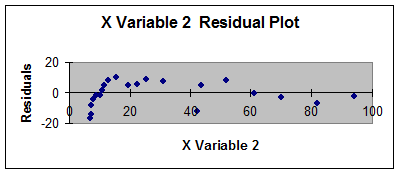
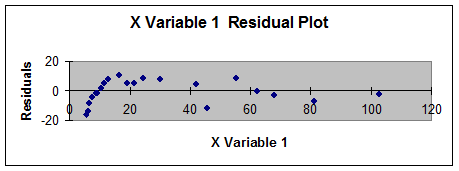
Interpretarea rezultatelor:
Tabelul SUMMARY OUTPUT
R = 0.9979 denota faptul ca intre PIB si import si export exista o legatura stransa in economia Frantei.
R2 0.9958 arata ca 99% din variatia PIB-ului se datoreaza importurilor si exporturilor. Comparant ce doua valori, deducem ca gradul de determinare in cadrul modelului de regresie bifactoriala a crescut de la 98% la 99%. Deci, influenta celor doua variabile (import si export), determina in proportie de 99% variatia PIB-ului in Franta, cresterea cu un procent fiind datorata exporturilor.
Abaterea medie patratica a erorilor ![]() 8.2096 reprezinta
abaterea punctelor fata de dreapta de regresie. Valoarea acestui indicator
demonstreaza ca functia de regresie este reprezentativa. Observam ca valoarea
abaterii medii patratica s-a micsorat de la 13 la 8 (cu aproximatie), asadar
modelul de regresie bifactorial este mult mai precis decat cel unifactorial.
8.2096 reprezinta
abaterea punctelor fata de dreapta de regresie. Valoarea acestui indicator
demonstreaza ca functia de regresie este reprezentativa. Observam ca valoarea
abaterii medii patratica s-a micsorat de la 13 la 8 (cu aproximatie), asadar
modelul de regresie bifactorial este mult mai precis decat cel unifactorial.
Numarul de observatii: 21
Tabelul ANOVA
Datele
furnizate de acest tabel in care este calculat testul F valideaza modelul de
regresie. Intrucat F = 2136.33685 iar
valoarea lui Significance F = 4.02 ![]() este mai mica de 0.05
atunci modelul de regresie construit este valid si poate fi utilizat in analiza
dependentei PIB-ului fata de importuri si exporturi.
este mai mica de 0.05
atunci modelul de regresie construit este valid si poate fi utilizat in analiza
dependentei PIB-ului fata de importuri si exporturi.
Intercept
fiind termenul liber, deci ![]() = -0.7416. In acest punct variabilele explicative sunt 0.
Deoarece
= -0.7416. In acest punct variabilele explicative sunt 0.
Deoarece ![]() = 10.5348 si P-Value este 3.98214
= 10.5348 si P-Value este 3.98214 ![]() < 0.05 atunci acest
coeficient este semnificativ. Intervalul de incredere pentru acest parametru
este 24.6867
< 0.05 atunci acest
coeficient este semnificativ. Intervalul de incredere pentru acest parametru
este 24.6867 ![]()
![]()
![]() 36.9858.
36.9858.
Coeficientul
![]() este -0.7416 .
Inseamna ca daca se majoreaza valoarea importurilor cu un miliard, in
conditiile in care exporturile raman constante, PIB-ul Frantei va scadea cu 0.7416.
Fiindca
este -0.7416 .
Inseamna ca daca se majoreaza valoarea importurilor cu un miliard, in
conditiile in care exporturile raman constante, PIB-ul Frantei va scadea cu 0.7416.
Fiindca ![]() = -0.82499 iar P-value = 0.42017 care este mai mare decat
0.05, rezulta ca coeficientul nu este semnificativ.
= -0.82499 iar P-value = 0.42017 care este mai mare decat
0.05, rezulta ca coeficientul nu este semnificativ.
Coeficientul
![]() este 5.25977. Inseamna
ca la cresterea exporturilor cu un miliard, in timp ce importurile raman
constante, PIB-ul Frantei se va majora cu 5.25977 miliarde euro. Deoarece
este 5.25977. Inseamna
ca la cresterea exporturilor cu un miliard, in timp ce importurile raman
constante, PIB-ul Frantei se va majora cu 5.25977 miliarde euro. Deoarece ![]() = 5.571606 si P-value = 0.000027 < 0.05 , inseamna ca
acest coeficient este semnificativ. Intervalul de incredere pentru acest
parametru este
= 5.571606 si P-value = 0.000027 < 0.05 , inseamna ca
acest coeficient este semnificativ. Intervalul de incredere pentru acest
parametru este
3.276437![]()
![]()
![]() 7.2431172.
7.2431172.
V. Anexe
In cele ce urmeaza vom estima valorile parametrilor modelului de
regresie utilizand metoda celor mai mici patrate ( M.C.M.M.P.):
yi = a + bxi + εi
![]() =
= ![]() +
+ ![]() , unde :
, unde :
![]() = valorile teoretice ale variabilei yi ( PIB) obtinute in functie de
valorile factorului x si de valorile estimatorilor a si b , respectiv
= valorile teoretice ale variabilei yi ( PIB) obtinute in functie de
valorile factorului x si de valorile estimatorilor a si b , respectiv ![]() si
si ![]() ;
;
εi = yi - ![]() = ( a -
= ( a - ![]() )+( b -
)+( b - ![]() ) = estimatiile valorilor variabilei reziduale
) = estimatiile valorilor variabilei reziduale
Astfel , M.C.M.M.P consta in minimalizarea functiei :
![]()
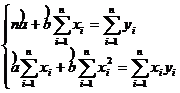 , n = 21
, n = 21
Rezolvarea sistemului necesita intocmirea urmatorului tabel:
|
PIB (y |
Importuri (x |
xi2 |
y2 |
( yi - |
( xi - |
xiX yi |
| |
| ||||||
|
TOTAL |
3536.1 |
647.7 |
|
|
|
|
|
Tabel 1: Valorile intermediare pentru estimarea modelului de regresie
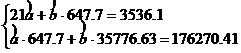 T
T ![]()
T relatia este de forma ![]() = 37.19 + 4.25xi
= 37.19 + 4.25xi
Dispunand de estimatiile
parametrilor se pot calcula valorile estimate ale variabilei endogene ![]() cu ajutorul relatiei
de mai sus, iar valorile variabilei reziduale vor rezulta din relatia :
cu ajutorul relatiei
de mai sus, iar valorile variabilei reziduale vor rezulta din relatia : ![]() = yi -
= yi - ![]() ( vezi tabelul
urmator, col.7 )
( vezi tabelul
urmator, col.7 )
|
yi |
xi |
a |
b |
bxi |
|
|
( yi - |
|
TOTAL |
|
|
|
|||||
Tabel 2: Valorile intermediare pentru testarea semnificatiei parametrilor modelului
|
|
|
285382.532 |
Pe baza acestor valori se pot calcula abaterea medie
patratica a variabilei reziduale![]() si abaterile medii patratice ale celor doi estimatori ,
si abaterile medii patratice ale celor doi estimatori , ![]() si
si ![]() :
:
![]() =
= ![]() =
= ![]() = 173.99, unde k = numarul parametrilor
= 173.99, unde k = numarul parametrilor
![]() =
= ![]() = 13.19
= 13.19
![]() =
= 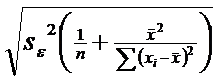 = 20.05
= 20.05
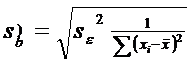 = 6.33
= 6.33
In cele ce
urmeaza, vom testa parametrii modelului de regresie ![]() si
si ![]() astfel:
astfel:
se stabileste ipoteza nula ![]() :
: ![]() = 0
= 0
![]() = 0
= 0
se stabileste ipoteza alternativa ![]() :
: ![]()
![]() 0
0
![]()
![]() 0
0
Vom calcula
testul care se dovedeste a fi unul de volum redus deoarece n = 21 < 30, deci
vom utiliza testul t, lucrand cu un
prag de semnificatie ![]() = 0,05;
= 0,05; ![]() = 37.19;
= 37.19; ![]() = 20.05 si
= 20.05 si ![]() = 4.25;
= 4.25; ![]() = 6.33
= 6.33
![]() =
= ![]() =
= ![]() =
= ![]() = 1.85
= 1.85
![]()
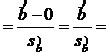
![]() = 0.67
= 0.67
![]() =
= ![]() =
= ![]() = 2,093
= 2,093
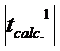 <
< ![]()
![]() 0.13 < 2,093
0.13 < 2,093
![]() <
< ![]()
![]() 0.59 < 2,093
0.59 < 2,093
Se accepta ipoteza nula conform careia parametrii modelului de regresie sunt 0.
1. Ipotezei nule ![]() : modelul nu este valid
: modelul nu este valid
2. Ipotezei alternative ![]() : modelul este valid
: modelul este valid
3. Se calculeaza testul F :
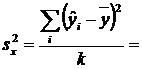 285382.532
285382.532
![]() =
= ![]() =
= ![]() = 173.99
= 173.99
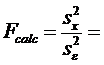
![]() = 1640.22
= 1640.22
Din tabela repartitiei F (Fisher ) se preia valoarea tabelata
pentru un prag de semnificatie ![]() =0,05
=0,05
![]() 4,38
4,38
|
Sursa de variatie |
Masura variatiei |
Nr. gradelor de libertate |
Dispersii corectate |
Valoarea testului F |
|
|
|
|
||||
|
Varianta dintre grupe |
SSR= 285382.532 |
k = 1 |
MSR = |
1640.22 | |
|
Varianta reziduala |
SSE= |
n - k - 1 = 19 |
MSE= |
_ |
|
|
Varianta totala |
SST = 289182.66 |
n - 1 = 20 |
MST = = 14459.133 |
_ |
|
Testul Fisher - Snedecor indica pe baza calculelor faptul ca
rezultatele sunt semnificative prin faptul ca Fcalc > Ftab T modelul este valid , pentru un prag de
semnificatie ![]() =0,05
=0,05
Intensitatea legaturii dintre cele doua variabile se face cu coeficientul de corelatie liniara Pearson
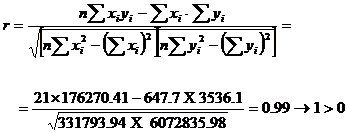
Coeficientul de
corelatie liniara este definit in intervalul ![]() , ceea ce inseamna ca valoarea obtinuta de 0.99 indica o legatura directa si puternica intre cele 2
variabile.
, ceea ce inseamna ca valoarea obtinuta de 0.99 indica o legatura directa si puternica intre cele 2
variabile.
1.Ipoteza nula![]() : r nu este semnificativ statistic
: r nu este semnificativ statistic
2.Ipoteza alternativa ![]() : r este semnificativ statistic
: r este semnificativ statistic
3.Se calculeaza statistica "t"
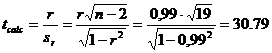
![]() 2,093
2,093
Pe baza calculelor de mai sus se respinge ipoteza nula ![]() , adica, coeficientul de corelatie este
semnificativ statistic, cu un prag de semnificatie
, adica, coeficientul de corelatie este
semnificativ statistic, cu un prag de semnificatie ![]() =0,05.
=0,05.
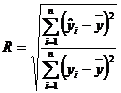
![]()
Verificarea semnificatiei raportului de corelatie se face cu ajutorul testului Fisher :
![]() =
= ![]()
![]()
![]() = 49
= 49
![]() =
=
Cum:
![]() T
R este semnificativ statistic
T
R este semnificativ statistic
Estimarea punctuala se face dupa modelul :
![]() = 37.19 + 4.25xi
= 37.19 + 4.25xi
![]() = 37.19 + 4.25
= 37.19 + 4.25![]() 5.7 = 233.965
5.7 = 233.965 ![]() 61.42 mld.Euro
61.42 mld.Euro
Ceea ce inseamna ca PIB-ul se ridica la valoarea de 61,42 mld.Euro tinand cont ca exporturile vor atinge valoarea de 46.3 mld.Euro.
Intervalul de incredere pentru valoarea prognozata a PIB-ului in perioada urmatoare se va realiza dupa modelul :
![]()
Pe
baza calculelor la punctele precedente , valoarea PIB-ului ( y ) se realizeaza dupa distributia Student ( n ![]() 30 ) si de
30 ) si de ![]() = 173.99. Din datele problemei
= 173.99. Din datele problemei ![]() = 5.7 astfel incat :
= 5.7 astfel incat :
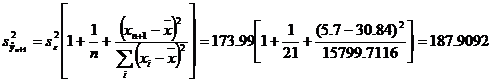
![]()
![]()
Intervalul
de incredere este : ![]()
Valoarea
prognozata a PIB-ului pentru perioada urmatoare s-a situat in intervalul ![]() cu o probabilitate de
95 %
cu o probabilitate de
95 %
|
Politica de confidentialitate |
| Copyright ©
2026 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |