Ciclul sau structura repetitiva
 De multe ori este necesara repetarea
unor operatii, in functie de anumite conditii.
De multe ori este necesara repetarea
unor operatii, in functie de anumite conditii.
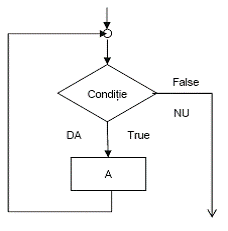
![]() Ciclul cu test initial sau structura repetitiva
conditionata anterior
Ciclul cu test initial sau structura repetitiva
conditionata anterior
Executia presupune parcurgerea urmatoarelor etape:
se evalueaza conditia;
daca rezultatul este adevarat, se executa secventa A, dupa care se trece din nou la evaluarea conditiei;
in caz contrar, se incheie executia ciclului.
Figura 2.17
Exprimarea in pseudocod a acestei structuri este: cat_timp conditie executa secventa A. Aceasta structura mai este cunoscuta ca structura de tip WHILE DO.
Observatie Figura 2.17 Atunci cand conditia este falsa de la inceput, secventa A nu se executa niciodata; in acest caz numarul de iteratii este zero (adica de cate ori a fost executata secventa A).
Exemplul 2.6
Sa se calculeze xn, unde x este un numar real, iar n un numar natural.
real x, putere
intreg n, i
citeste x, n
i=1
putere = 1
cat_timp i<=n executa
putere =putere * i
i = i+1
scrie putere
stop
Variabila "putere" este folosita pentru a pastra puterea i a lui x, i fiind o variabila intreaga ce "numara" puterea la care este ridicat x, fiind denumita variabila de tip contor.
Acest concept a fost dezvoltat de E. W. Dijkstra in lucrarile sale, iar ulterior si de alti specialisti, ca de exemplu N. Wirth si C. A. R. Noare si s-a aflat la baza ideii care a condus in anii '70 la conceptul de programare structurata. El reprezinta un stil de programare care se impune si in prezent. Un efect imediat al programarii structurate este ridicarea productivitatii in programare si cresterea fiabilitatii programelor.
Prin algoritm structural intelegem un algoritm care are o structura de control realizata cu ajutorul celor trei structuri amintite mai sus. Ulterior s-au admis inca doua structuri, si anume:
- structura selectiva
- structura repetitiva (ciclica) conditionata posterior.
Introducerea acestor structuri permite o flexibilitate mai mare in programare. In acest fel, programarea structurata reprezinta un stil de programare care contribuie la realizarea de programe cu o structura clara si care pot fi usor depanate si intretinute.
![]() Ciclul cu test final sau structura repetitiva
conditionata posterior
Ciclul cu test final sau structura repetitiva
conditionata posterior
Executia presupune parcurgerea urmatoarelor etape:
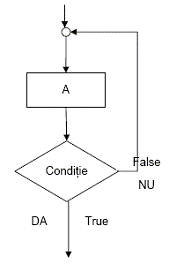 se executa secventa A
se executa secventa A
se evalueaza conditia;
daca rezultatul este fals, se continua cu primul pas;
in caz contrar, se incheie executia ciclului.
Exprimarea in pseudocod a acestei structuri este:
repeta
secventa A
pana_cand conditie
Aceasta structura mai este cunoscuta ca structura de tip REPEAT UNTIL
Observatie
Deoarece testarea conditie se face la sfarsit, secventa se executa cel putin o data (numarul de iteratii este mai mare decat zero).
Figura 2.18
 Structura
selectiva
Structura
selectiva
Exprimarea in pseudocod a acestei structuri este:
case <expr>
c1:
bloc 1;
break;
c2:
bloc 2;
break;
cn:
bloc n;
break;
[default
bloc n+1]
end
Schema logica este urmatoarea :
Fig. 2.19
Exemplul 2.7
Sa se calculeze n! (factorialul numarului n, adica n!=1*2**n).
Pentru rezolvare sunt necesare variabilele de tip intreg n, citit de la tastatura, i, variabila necesara contorizarii pasilor efectuati in calcularea produsului si variabila fact, care va memora valoarea produsului calculat.
intregi n, i, fact
citeste n
i=1
fact=1
repeta
fact=fact*i
i=i+1
pana_cand i>n
scrie fact
stop
Exemplul 2.8
Sa se calculeze suma primelor n numere naturale.
Pentru rezolvare sunt necesare variabilele intregi n, i, s, primele doua variabile avand aceeasi semnificatie ca la problema precedenta, iar s este variabila necesara pastrarii valorii sumei numerelor naturale de la 1 la n.
intregi n, i, s
citeste n
i=1
s=0
repeta
s=s+i
i=i+1
pana_cand i>n
scrie s
stop
Sa probam functionalitatea algoritmului pentru n=3:
i ia valoarea 1 iar s ia valoarea 0; ("se initializeaza" cu aceste valori)
i se adauga la vechea valoare a lui s s=0+1=1
i creste cu o unitate ("se incrementeaza") i=1+1=2
se compara i cu n; deoarece i este mai mic decat n, se trece la repetarea celor doi pasi;
i se adauga la vechea valoare a lui s s=1+2=3
i creste cu o unitate ("se incrementeaza") i=2+1=3
se compara i cu n; deoarece i nu este mai mare decat n, se trece la repetarea celor doi pasi;
i se adauga la vechea valoare a lui s s=3+3=6
i creste cu o unitate ("se incrementeaza") i=3+1=4
i este mai mare decat n, deci se opreste executia ciclarii, se tipareste valoarea sumei s si algoritmul se incheie.
Observatie:Daca se compara aceasta problema cu precedenta, se observa o asemanare in rezolvarea lor, si anume o parte de initializare a variabilelor si o ciclare pentru calculul celor doua valori: factorial, respectiv suma. Diferentele constau in valorile de initializare a factorialului (1, deoarece se calculeaza un produs), respectiv a sumei (s=0) si operatiile de calcul a celor doua variabile; inmultire, respectiv adunare.
![]() Ciclul
cu contor sau structura
repetitiva cu numar cunoscut de pasi (iteratii)
Ciclul
cu contor sau structura
repetitiva cu numar cunoscut de pasi (iteratii)
Aceasta structura repetitiva este folosita in cazurile in care este cunoscut numarul de iteratii ale structurii si modul in care se modifica o variabila ce controleaza executia acestuia, denumita contor.
Exprimarea in pseudocod a acestei structuri este:
pentru contor=vi, vf, pas executa
secventa A
vi, vf reprezinta valorile initiale, respectiv finale ale variabilei contor, iar pas este valoarea cu care se modifica contor la terminarea executiei secventei A; daca nu este precizata nici o valoare pentru pas, aceasta este implicit 1. Aceasta structura este echivalenta cu:
contor=vi
cat_timp contor<=vf executa
secventa A
contor=contor+pas
Exemplul 2.9
Sa se calculeze suma primelor n numere naturale, folosind ciclul cu contor.
Algoritmul a fost explicat in cadrul exemplului 2.8. Rezolvarea in acest caz este:
citeste n
s=0
pentru i=1, n executa
s=s+i
scrie s
Se observa in acest caz ca, in cadrul structurii repetitive nu mai apare operatia de incrementare a variabilei contor i, aceasta fiind inclusa in executia instructiunii.
Selectia: reprezinta calculul unei expresii, si in functie de rezultatul acesteia, algoritmul va continua pe una din ramurile posibile. Expresia trebuie sa fie definita intr-un tip de date cu valori finite.
Pseudocod: case expresie
c1: secventa_1;
c2: secventa_2;
cn: secventa_n;
rest: secventa_rest;
endcase;
![]() Test de autoevaluare 2.4
Test de autoevaluare 2.4
Scrieti algoritmul de rezolvare a urmatoarelor probleme; puteti folosi reprezentarea algoritmilor prin scheme logice sau pseudocod. Rezolvarea fiecarei probleme valoreaza 20 de puncte.
1. Sa se scrie algoritmul pentru calcularea sumei primelor n numere naturale impare, unde n este un numar natural strict pozitiv, dat.
2. Se citeste un sir de numere naturale pana la introducerea valorii zero. Sa se determine media aritmetica a numerelor pare introduse si produsul numerelor impare.
3. Se citeste un sir de numere naturale pana la introducerea valorii zero. Sa se determine suma numerelor de pe pozitiile pare (suma dintre al doilea, al patrulea, etc) si produsul numerelor de pe pozitiile impare (produsul dintre primul, al treilea, al cincilea, etc).
4. Sa se determine valoarea urmatoarelor expresii, unde n este un numar natural dat:
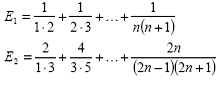
Dandu-se a, b si c, coeficientii unei ecuatii de gradul doi, sa se calculeze:
![]()
unde n este un numar natural dat, fara a se rezolva ecuatia (tinand cont de valorile lui P si S).
 Lucrarea de verificare Nr. 2.
Lucrarea de verificare Nr. 2.
Rezolvati urmatoarele probleme. Acestea trebuie sa fie reprezentate prin scheme logice sau pseudocod. Fiecare problema valoreaza 20 puncte.
1. Se dau 4 numere reale a, b, c si d.
a) Sa se efectueze permutarea circulara la dreapta cu o pozitie a valorilor sirului de numere, astfel incat la afisarea valorilor acestora sa fie tiparite in ordinea d, a, b, c;
b) Sa se efectueze permutarea circulara la stanga cu o pozitie a valorilor sirului de numere, astfel incat la afisarea valorilor acestora sa fie tiparite in ordinea b, c, d, a,;
c) Sa se inverseze sirul de numere, adica sa li se interschimbe valorile astfel incat la afisarea lor sa se afiseze d, c, b, a.
Se va folosi o singura variabila auxiliara.
2. Se considera doua unghiuri A si B, fiecare masurat in grade, minute si secunde. Sa se scrie un algoritm care permite calcularea sumei si diferentei celor doua unghiuri, rezultatul afisandu-se in aceeasi forma (grade, minute si secunde). Presupunem ca unghiul A este mai mare sau egal decat unghiul B.
3. Sa se determine cea mai mare si cea mai mica valoare dintr-un sir de 4 numere reale citite de la tastatura.
4. Se dau 4 numere intregi a, b, c, si d. Sa se afiseze valorile acestora in ordine descrescatoare.
 5.
Se citeste un sir de numere reale de la tastatura, pana la
introducerea valorii zero. Sa se determine cate dintre ele,
impartite la un numar dat k dau un rest egal cu r. (k
si r se citesc si ele de la tastatura).
5.
Se citeste un sir de numere reale de la tastatura, pana la
introducerea valorii zero. Sa se determine cate dintre ele,
impartite la un numar dat k dau un rest egal cu r. (k
si r se citesc si ele de la tastatura).
|
Politica de confidentialitate |
| Copyright ©
2025 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |