Reprezentarea algoritmilor
Limbajul natural nu permite o descriere suficient de riguroasa a algoritmilor, complexitatea descrierilor in limbaj natural. De aceea, pentru reprezentarea algoritmilor se folosesc diferite forme de reprezentare caracteristice, in fapt limbajele specializate. In general, notatia folosita pentru reprezentarea algoritmilor trebuie sa satisfaca urmatoarele cerinte:
1. Sa permita exprimarea cat mai naturala a rationamentelor umane, sa fie usor de invatat si de folosit;
2. Sa reflecte caracteristicile limbajelor de programare de nivel inalt pentru a usura codificarea algoritmilor.
Formele conventionale cele mai folosite in reprezentarea algoritmilor sunt:
schemele logice sau organigramele
limbajele pseudocod.
Principala calitate a acestora este posibilitatea de a evidentia cu claritate fluxul controlului algoritmilor, adica succesiunile posibile ale actiunilor.
Astfel, schemele logice utilizeaza pentru aceasta sageti de legatura intre diversele forme geometrice care simbolizeaza diversele tipuri de actiuni, in timp ce limbajele pseudocod folosesc cuvinte - cheie, adica niste cuvinte cu inteles prestabilit ce identifica operatia care se executa, si cateva reguli simple de aliniere a textului scris.
In continuare sunt prezentate blocurile ce pot intra in componenta unei scheme logice.
R Blocul delimitator are forma unei elipse alungite. El se foloseste pentru a marca inceputul sau sfarsitul schemei logice. Daca blocul este folosit la inceputul schemei logice, atunci in interiorul sau se scrie cuvantul START, iar daca blocul este folosit la sfarsitul schemei logice, atunci in interiorul sau se scrie cuvantul STOP. Figura 2.1 contine blocul delimitator folosit in cele doua situatii.
Fig. 2.1
R Blocul de intrare / iesire are forma unui paralelogram. Acest bloc se foloseste la introducerea datelor in calcule si afisarea rezultatelor.
De obicei, datele de intrare ale unei probleme se introduc initial, cu ajutorul tastaturii, intr-o zona de memorie numita zona tampon. De aici ele sunt preluate de program. Aceasta operatie de preluare a datelor dintr-o zona tampon se numeste operatie de citire. Datele preluate din zona tampon sunt introduse in memoria interna a calculatorului. Aceasta operatie se precizeaza in schemele logice prin cuvantul CITESTE. In figura 2.2. apare o comanda de citire. Aceasta comanda cere sa se citeasca valorile variabilelor a si b si sa se introduca aceste valori in memoria interna.
![]()
Fig. 2.2
Operatia de preluare a valorilor unor variabile din memoria interna si afisarea lor pe ecranul calculatorului se numeste operatie de scriere. De aceea, aceasta operatie se precizeaza in schemele logice prin cuvantul SCRIE. In figura 2.2. apare o comanda de scriere. Aceasta comanda cere sa se scrie valoarea variabilei x pe ecranul monitorului.
Blocul de calcul se foloseste pentru a preciza calculele care se fac. In blocurile de acest tip apar comenzi de forma: v=e, unde v este o variabila, iar e este o expresie de tip compatibil cu v. La intalnirea comenzii v=e se determina valoarea expresiei e, se converteste, daca este cazul, valoarea lui e la o valoare de tipul lui v si se atribuie aceasta valoare variabilei v.
Figura 2.3. contine mai multe blocuri de calcul. Aici am presupus ca toate variabilele sunt de tip numeric. In primul bloc se atribuie variabilei s valoarea 2. Al doilea bloc contine expresia c+3. Aici am presupus ca c are o valoare numerica rezultata dintr-o operatie anterioara. Valoarea expresiei se converteste, daca este cazul, la o valoare de tipul lui a si se atribuie lui a. In al treilea bloc apare expresia b+3. Valoarea acestei expresii se atribuie lui b. Prin urmare, dupa executia acestei comenzi, valoarea lui b se mareste cu 3. Asadar, semnul = care apare in blocurile de calcul nu trebuie confundat cu semnul = din matematica, pentru ca se ajunge la ceva fara sens. In fine, in ultimul bloc se cere sa se atribuie lui m valoarea 2.3. Daca m este o variabila de tip intreg, atunci numarul 2.3 este convertit la numarul intreg 2 si apoi este atribuit variabilei m.

Fig. 2.3
R Blocul de decizie are forma unui romb. In interiorul sau se scrie o conditie care determina ramificarea calculelor. Figura 2.4. contine un asemenea bloc. Conditia din blocul de decizie se citeste ca o propozitie interogativa.
Astfel, in cazul din figura 2.4. citim: Este y egal cu x ? Daca raspunsul la aceasta intrebare este da, atunci se iese din blocul de decizie pe ramura pe care este scris cuvantul DA. Dimpotriva, daca raspunsul la intrebarea de mai inainte este nu, atunci se iese din blocul de decizie pe ramura pe care este scris cuvantul NU.

Fig. 2.4
R Bloc de procedura (fig.2.5) Acest bloc se utilizeaza pentru punerea in evidenta a unor subalgoritmi (parti dintr-un algoritm) in interiorul acestuia se indica ce anume se executa fara a explicita pasii elementari respectivi
![]()
Fig.2.5
![]()
R Blocul conector are forma de cerc. El se foloseste pentru a conecta diferite secvente ale unei scheme logice si poate sa fie:
-conector in cadrul aceleiasi pagini (fig 2.6). Acest conector leaga punctele de intrerupere ale unei scheme logice in cadru1 aceleiasi pagini.
![]()
![]()
![]()
![]() Fig.2.6
Fig.2.6
-conector pentru trecerea la alta pagina (fig.2.7). Se plaseaza la sfarsitul, respectiv inceputul unei pagini.
![]()
![]()
![]()
![]() Fig. 2.7
Fig. 2.7
R
![]() Sageata (fig. 2.8). Toate blocurile
mentionate mai sus se leaga intre ele cu ajutorul unei
sageti (orizontale sau verticale) care indica sensul
prelucrarii informatiei
Sageata (fig. 2.8). Toate blocurile
mentionate mai sus se leaga intre ele cu ajutorul unei
sageti (orizontale sau verticale) care indica sensul
prelucrarii informatiei
![]()
Fig. 2.8
R Semnul de atribuire. In descrierea proceselor de calcul cu ajutorul schemelor logice se foloseste semnul de atribuire (doua puncte si egal). ": ="
In dreapta semnului de atribuire se scriu anumite marimi a caror valoare numerica este cunoscuta, iar in stanga semnului de atribuire se scriu variabilele care iau valorile ce figureaza in membrul drept. Semnul = care apare in blocul de decizie are sens de comparatie. El nu se va confunda cu semnul = din blocurile de calcul. Pentru scrierea conditiilor se mai folosesc si celelalte semne de comparatie din matematica: <, ≤, >, ≥ si ≠.
Alte simboluri folosite:
![]()
Fisier pe banda magnetica
![]()
![]()
Fisier pe disc magnetic
![]()
![]() Disc flexibil
Disc flexibil

Dispozitiv de afisare (display)
![]()
Terminal cu tastatura
![]()
Exemple de scheme logice
Sa se descrie cu ajutorul unei scheme
logice un algoritm de calcul, pentru expresiile: E E E Pentru X,Y Solutie:Informatia initiala o
constituie valorile lui X si Y, iar informatia finala o
constituie valorile lui E Se observa ca valorile acestora
se pot calcula numai intr-o anumita ordine. Schema logica ce descrie algoritmul de
calcul al expresiilor este data in fig.2.9
a) schema
logica liniara
![]() = X
= X![]() + Y
+ Y![]()
![]() = X + Y + E
= X + Y + E![]()
![]() = XY +
E
= XY +
E![]() + E
+ E![]()
![]() R
dati.
R
dati.![]() , E
, E![]() , E
, E![]()
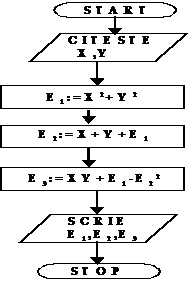
Fig.2.9
a) schema logica ramificata
Sa se descrie cu ajutorul unei scheme logice, un algoritm pentru calculul radacinilor ecuatiei de gradul II.
![]() a,b,c
a,b,c ![]() R
R
Solutie: Informatia initiala o constituie valorile coeficientilor a, b si c, iar informatia finala valorile radacinilor ecuatiei.
In stabilirea algoritmului se disting urmatoarele situatii:
1. ![]() - ecuatia este nedeterminata
- ecuatia este nedeterminata
2. ![]()
![]() - ecuatia este
imposibila
- ecuatia este
imposibila
![]() - ecuatia are o
solutie reala X
- ecuatia are o
solutie reala X![]() = -c/b
= -c/b
4. ![]() -
natura radacinilor ecuatiei de gradul II este data de
valoarea determinantului
-
natura radacinilor ecuatiei de gradul II este data de
valoarea determinantului ![]()
daca
![]() - ecuatia are radacini reale si distincte
- ecuatia are radacini reale si distincte
notate cu ![]() +
+ ![]()
![]()
![]()
daca
![]() - ecuatia are
radacini reale si egale notate cu:
- ecuatia are
radacini reale si egale notate cu:
![]()
daca
![]() ecuatia are
radacini complexe notate cu:
ecuatia are
radacini complexe notate cu:
![]() si
si ![]() , unde:
, unde: ![]() ;
; ![]()
Schema
logica ce descrie algoritmul de solutionare a ecuatiei de gradul
II este data de fig 2.10. pentru cazul ![]()
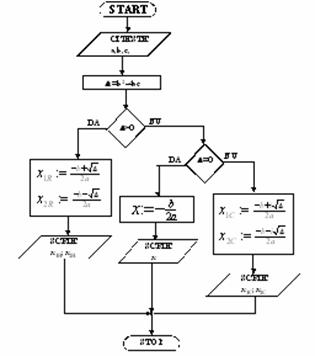
Fig.2.10
c) schema logica ciclica
Sa se descrie cu ajutorul unei scheme logice un algoritm pentru calculul sumei
![]()
Solutie: Informatia initiala o constituie
valorile lui ![]() ,
, ![]() , iar informatia finala valoarea lui S. Vom calcula
aceasta suma, calculand din aproape in aproape suma a cate doua
numere, astfel:
, iar informatia finala valoarea lui S. Vom calcula
aceasta suma, calculand din aproape in aproape suma a cate doua
numere, astfel:
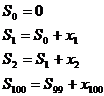
Generalizand, rezulta urmatoarea
formula de recurenta:![]() ;
; ![]()
Numarul pasilor algoritmul este 100, iar schema logica ce descrie algoritmul este data in fig.2.11

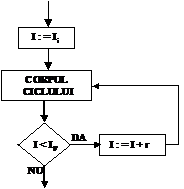

Fig.2.11
Prezentam la final o schema logica care contine toate blocurile pe care le-am descris inainte. Este vorba de schema logica de rezolvare a ecuatiei ax+b=0 cu a si b numere reale. Evident, daca a=0 si b=0, atunci ecuatia este satisfacuta de orice x. Prin urmare, in acest caz ecuatia are o infinitate de solutii. Daca a = 0 si b ≠ 0, atunci apare o incompatibilitate. In fine, daca a ≠ 0, atunci ecuatia are o singura solutie: x = -b/a, pentru orice b. Schema logica de rezolvare a problemei apare in figura 2.12. Asa cum observam, blocurile schemei logice sunt conectate intre ele prin linii prevazute cu sageti. Aceste sageti indica ordinea de parcurgere a blocurilor( Fig. 2.12)
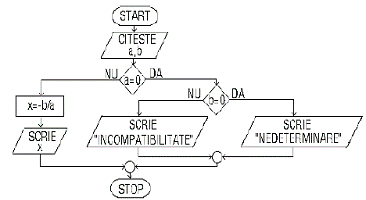 Schema logica de rezolvare a
ecuatiei ax+b=0 contine o comanda pentru citirea datelor.
Aceasta comanda cere sa se citeasca valorile variabilelor a
si b. Pe baza acestei scheme putem alcatui un program care
sa rezolve o ecuatie de forma ax+b=0 pentru orice valori ale
lui a si b. In primul bloc de decizie din schema logica
apare conditia a=0. Evident, conditia a=0 poate fi
adevarata sau falsa. Daca conditia a=0 este
adevarata, atunci din blocul de decizie se iese pe ramura pe care
este scris cuvantul DA, iar daca conditia a=0 nu este
adevarata, atunci din blocul de decizie se iese pe ramura pe care
este scris cuvantul NU.
Schema logica de rezolvare a
ecuatiei ax+b=0 contine o comanda pentru citirea datelor.
Aceasta comanda cere sa se citeasca valorile variabilelor a
si b. Pe baza acestei scheme putem alcatui un program care
sa rezolve o ecuatie de forma ax+b=0 pentru orice valori ale
lui a si b. In primul bloc de decizie din schema logica
apare conditia a=0. Evident, conditia a=0 poate fi
adevarata sau falsa. Daca conditia a=0 este
adevarata, atunci din blocul de decizie se iese pe ramura pe care
este scris cuvantul DA, iar daca conditia a=0 nu este
adevarata, atunci din blocul de decizie se iese pe ramura pe care
este scris cuvantul NU.
Desigur, si conditia b=0 care apare in celalalt bloc de decizie al schemei logice determina ramificarea calculelor intr-un fel sau altul. In fine, sa mai observam ca in blocul de calcul apare scris x = -b/a. Evident, x = -b/a nu este o conditie. Acum se cere sa se determine valoarea lui -b/a si sa se atribuie valoarea calculata lui x.
Schema
logica pe care o analizam contine trei drumuri care pornesc de
Facem intai verificarea schemei pentru a=2 si b=-8. Prin urmare, dorim sa rezolvam ecuatia 2x-8=0. Pe schema logica parcurgem pasii urmatori:

Consideram acum cazul in care a=0 si b=-6. Asadar, este vorba de ecuatia 0x - 6=0. Acum avem o incompatibilitate. Pe schema logica parcurgem pasii urmatori:

In fine, consideram cazul in care a=0 si b=0. Asadar, este vorba de ecuatia 0x+0=0. Este vorba de o nedeterminare. Pe schema logica parcurgem pasii urmatori:

Schema pe
care am prezentat-o aici este foarte simpla. De aceea, a fost posibil
sa o verificam cu seturi de date corespunzatoare tuturor
drumurilor care duc de
|
Politica de confidentialitate |
| Copyright ©
2025 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |