
Calitatea vietii in Uniunea Europeana
1. Datele
Datele analizate sunt prezentate in matricea de mai jos .Acestea sunt preluate din cartea "Europe in figures - Eurostat yearbook " , editia 2006-2007 si poate fi gasita si la adresa de internet ec.europa.eu/eurostat .
|
TARILE |
Dens |
Sperm |
Sperf |
Moinf |
Energie |
Nr pat |
Mob |
Stud |
Rata |
|
|
Belgia | ||||||||||
|
Cehia | ||||||||||
|
Danemarca | ||||||||||
|
Germania | ||||||||||
|
Estonia | ||||||||||
|
Grecia | ||||||||||
|
Spania | ||||||||||
|
Franta | ||||||||||
|
Irlanda | ||||||||||
|
Italia | ||||||||||
|
Cipru | ||||||||||
|
Letonia | ||||||||||
|
Lituania | ||||||||||
|
Luxemburg | ||||||||||
|
Ungaria | ||||||||||
|
Malta | ||||||||||
|
Olanda | ||||||||||
|
Austria | ||||||||||
|
Polonia | ||||||||||
|
Portugalia | ||||||||||
|
Slovenia | ||||||||||
|
Slovacia | ||||||||||
|
Finlanda | ||||||||||
|
Suedia | ||||||||||
|
U.K. | ||||||||||
|
Bulgaria | ||||||||||
|
Romania |
|
|
Criteriile urmarite in tabel , pentru aceasta analiza referitoare la calitatea vietii in U.E., sunt alese astfel incat sa fie atinse cele mai relevante aspecte din viata omului , din secolul 21.
Dens - densitatea populatiei
Sperm/Sperf - speranta de viata la nastere pentru barbati si femei
Moinf - mortalitatea infantila la 1000 loc
Energie - energie electrica consumata , exprimata in GWh / 1000 loc
Nr_pat - numarul paturilor din spitale la 100.000 loc , am ales acest indicator in detrimentul numarului de medici , deoarece multe tari nu au statistici puse la punct in aceasta privinta .
Mob - numarul de abonamente de telefonie mobila la 100 loc , din nou din multitudinea de tipuri de tehnologii prezente , telefonia mobila ofera cele mai multe date , in toate tarile analizate .
Stud - numarul de elevi si studenti la 1000 loc
Rata - rata inflatiei
Aceste date sunt luate din perioada 2004 -2005 , cu anumite exceptii unde s-au folosit date mai vechi , nefiind puse la dispozitie datele actualizate , statisticile respective inca nu sunt valabile .
Scopul analizei asupra acestei matrice de date este de a determina care sunt indicatorii cu adevarat relevanti , dar si de a realiza o clasificare a tarilor si nu numai a criteriilor . Pentru acest lucru vor fi utlizate Tehnica de Analiza in Componente Principale si Algoritmul Ierarhic de Clasificare .
2. Etapele teoretice
A. Analiza in Componente Principale
Componentele principale ofera o tehnica pentru a reexprima variabilele( vectorii x1 , x2 xp) prin altele noi ( notate z1,z2,,zs) , cu s<=p , care sa indeplineasca urmatoarele proprietati :
sa fie ortogonale 2 cate 2
fiecare dintre acestea sa captureze o cantitate cat mai mare din imprastierea totala a valorilor variabilei X .
Pasii algoritmului sunt urmatorii:
Pasul 1. Se standardizeaza datele din matricea de date, folosind mediile si abaterile medii patratice ale variabilelor.
Pasul 2. Se calculeaza, din datele standardizate, matricea corelatiilor, fie ea R.
Pasul 3. Se identifica primele q valori proprii ale matricei R a corelatiilor (in ordine descrescatoare). Fie ele λ1 ≥ λ 2 ≥ ≥ λ q.
Pasul 4. Prima axa factoriala f 1 este data de vectorul propriu de norma 1 asociat valorii proprii λ1. A doua axa factoriala f 2 este data de vectorul propriu de norma 1 asociat valorii proprii λ2 , s.a.m.d. Formam matricea a vectorilor proprii. F = ( f 1, f 2 ,, f q )
Pasul 5. Matricea C = (C1,C2 ,,Cq ) a componentelor principale - variabilelor factoriale - se obtine din matricea vectorilor proprii F ai matricei R si din matricea X, adica C = X F
Pasul 6. Dupa parcurgerea pasului 5 pentru toate cele q (< p) axe factoriale,cantitatea totala de informatie din norul de puncte recuperata de subspatiul factorial descris de axele f 1, f 2 , , f q este λ1 + λ2 + .. + λq .
Un mod practic de apreciere a calitatii ajustarii norului de puncte prin acest subspatiu este calculul raportului
![]()
Cum acest raport exprima, procentual, cantitatea de informatie recuperata. Evident, cu cat 0 ≤ τq ≤ 100 , τq este mai apropiat de valoarea maxima 100, cu atat norul de puncte este ajustat mai bine prin subspatiul de dimensiune q.
B Analiza de tip Cluster
Metodele de clasificare sau de analiza "cluster" au ca scop gruparea indivizilor, identificati printr-o serie de atribute - variabile numerice - intr-un numar cat mai restrans de clase omogene. Ceea ce le caracterizeaza este faptul ca realizeaza o analiza globala a indivizilor ce sunt studiati printrun numar mare de variabile, iar ipotezele cerute sunt minime. Mai precizam faptul ca obiectul clasificarii nu-l reprezinta numai indivizii ci poate fi si variabilele .
Se doreste a se realiza clase in asa fel incat indivizii apartinand unei aceleiasi clase sa fie cat mai asemanatori intre ei prin valorile variabilelor lor in timp ce clasele constituite sa fie cat mai diferite. Putem spune ca efectuarea unei analize "cluster" presupune parcurgerea a doua etape:
a) alegerea unei masuri de proximitate, mai precis, definirea unei masuri de apropiere dintre indivizi pe baza tuturor variabilelor observate;
b) precizarea unor reguli de construire a claselor asa incat diferenta intre acestea sa fie cat mai mare, in timp ce indivizii aflati in acelasi grup sa fie cat mai apropiati.
Tehnici de clasificare :
1) Analiza claselor ierarhice este o metoda de grupare "ierarhica" in care fiecare clasa este in totalitate continuta in alta clasa. Nu este ceruta nici o informatie a priori despre numarul claselor, iar odata ce un individ a fost asociat unei clase, el va ramane acolo. Nu este recomandata a fi utilizata pentru baze de date mari, cu multi indivizi.
2) Analiza claselor disjuncte este o tehnica ne-ierarhica, ce recurge la o clasificare iterativa.Initial toti indivizii se grupeaza arbitrar in clase. Urmeaza apoi o repartizare a fiecarui individ la o clasa, in functie de similaritatea individului respectiv cu cei din clasa respectiva. Procedeul este iterativ si se termina atunci cand nu mai constatam realocari intre clase. Procedeul este mai eficient pentru baze de date mari, iar pentru rapiditate s-ar impune cunoasterea a priori a numarului de clase.
3) Clasificarea pe baza mediei . Este o tehnica de clasificare in clase disjuncte, centrul fiecarei clasei fiind obtinut "dinamic" ca medie a indivizilor din clasa respectiva. Tehnica k-mean are ca obiectiv, la fiecare iteratie, reducerea variantei indivizilor din interiorul fiecarei clase si maximizarea variantei dintre clase.
Indicele de proximitate este un numar ce exprima asemanarea (similaritatea) - sau deosebirea (disimilaritatea) - existenta intre doi indivizi, luand in considerare toate valorile observate asupra variabilelor lor. Astfel, putem sa spunem ca proximitatea intre indivizi este masurata printr-o matrice D(n × n) in care un element dij exprima similaritatea (disimilaritatea) intre individul i si individul j. Exista mai multe moduri de construire a matricei de proximitate, unul dintre fiid acesta :
* Sa presupunem ca datele initiale sunt exprimate printr-o matrice de forma indivizi × variabile. Fie doi indivizi i si j si liniile corespunzatoare lor in matricea de date. Mai precis, fie xi linia corespunzatoare individului i si xj linia corespunzatoare individului j. Pentru cei doi indivizi putem calcula distanta data de norma Lr.
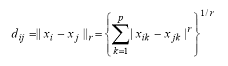
Pt r=2 , aceasta este distanta euclidiana . Aceasta distanta poate fi folosita ca o masura de proximitate, ea masurand disimilaritatea intre indivizi. Mai precis, cu cat distanta intre indivizi este mai mare, cu atat disimilaritatea intre acestia este mai mare . Se mai observa faptul ca distanta astfel calculata ne va conduce la o matrice de proximitate simetrica, avand 0 pe diagonala principala.
Atunci cand dorim sa evaluam proximitatea intre clase de indivizi, putem recurge la mai multe proceduri :
a) Metoda vecinilor celor mai apropiati. Prin aceasta, distanta dintre doua clase este asimilata cu distanta dintre elementele cele mai apropiate intre ele (elemente apartinand, evident, la grupuri diferite). Utilizarea acestei metode poate conduce la riscul
aparitiei de grupuri foarte eterogene, deoarece nu luam in calcul elementele extreme ale clasei.
b) Metoda vecinilor celor mai departati. Prin aceasta, distanta dintre doua clase este asimilata cu distanta dintre elementele cele mai departate intre ele.
c) Metoda agregarii prin medii. Aceasta consta in evaluarea distantei intre doua clase pornind de la "centrele lor de greutate". Desi aceasta metoda este foarte logica, ea cere multe calcule suplimentare in comparatie cu primele doua. De aceea, de multe ori este mai indicat a se utiliza una dintre metodele anterioare.
3. Aplicatia pe baza datelor din matricea de la primul punct , utilizand mediul SPSS
A. Analiza in Componente Principale
Inainte de a efectua de a aplica efectiv aceasta tehnica , trebuie mentionat ca aceste date sunt variabile continue si de aceea putem calcula indicatorii de centrare si imprastiere pentru fiecare clasa , indicatori cum sunt min , max , amplitudinea , media sau abaterea standard , dupa cum urmeaza in Tab 1 .
Se poate observa diferenta dintre aceste criterii de ordin cantitativ , si luand in considerare si abaterea standard din tabel e de preferat sa lucram cu datele standardizate , pentru o mai buna analiza , datele standardizate sunt trecute in cadrul anexelor .
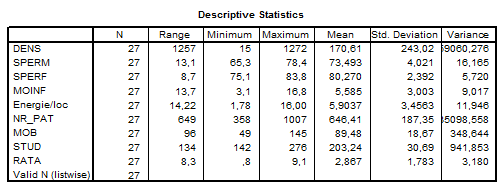
Tab 1 .
Pentru a analiza independenta dintre acesti indcatori , se calculeaza matricea corelatiilor .
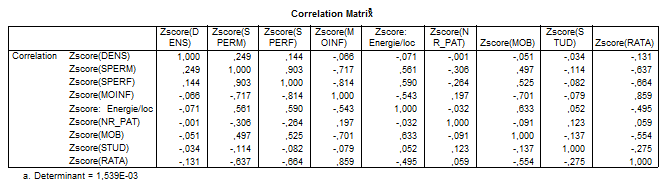
Dupa cum se observa , exista cativa indicatori intre care apar legaturi destul de puternice , cum sunt sperm , sperf si moinf , rata si sperm /sperf , rata si mob , energie si mob - in toate aceste cazuri sunt coeficienti de peste 0,6 , ajungand intre speranta de viata la femei si barbati la 0,9 si mai redusa cum aminteam de 0,66 intre speranta de viata la femei si rata inflatiei . Este destul de greu de precizat ce criterii e de preferat sa se elimine , de aceea mai bine se determina care ar fi acei indicatori cheie , daca se afla printre acestia .
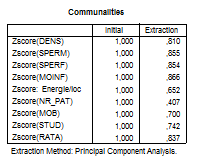
In tabelul alaturat , sunt trecuti indicatorii , iar pe coloana intitulata "Extraction" sunt valorile exprimate zecimal , cuprinse in intervalul [0,1] , valori ce exprima cantitatea de informatie recuperata de catre fiecare indicator , prin aplicarea ACP , daca aceasta cantitate este < 0,4 se poate decide renuntarea la indicele respectiv , in cazul de fata doar nr_pat are o valoare mai redusa , dar poate fi mentinut in continuare in analiza .
Un alt tabel foarte important este urmatorul , deoarece prezinta cantitatea de informatie recuperata prin intermediul primelor 3 componente . De mentionat , ca in cadrul ACP , se poate specfica un anumit numar de componente , iar in cazul de fata s-a ales 3 .
In coloana " Initial Eigenvalues" sunt trecute valorile proprii , in ordine descrecatoare , ele redand cantitatea de informatie extrasa prin intermediul fiecarei componente - adica noii indicatori , acei indiatori sintetici care sumarizeaza informatia din indicatorii initiali . Primele 3 componente extrag 74,68 % din informatia adusa de indicatorii initiali . Este un scor bun , care permite continuarea analizei , se observa , ca in cazul in care ar fi fost alese 4 componente s-ar fi ajuns la peste 84 % din informatia initiala - o alternativa viabila si aceasta deoarece au fost luati in calcul 9 indici .

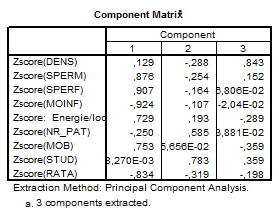

Rezultatele preliminare care ne indica fiecare componenta de la ce indici a preluat informatia sunt prezentate in tabelul Component Matrix si este foarte clar ca prima componenta recupereaza informatie de la indicatorii de speranta de viata si mortalitate infantile obtinandu-se valori de aprozimativ 0,9 , totusi aceasta componenta este influentata puternic si de energie , mob si rata - avand ponderi semnificativede peste 0,7 .
Componenta 2 preia informatii de la stud in special 0,78 si intr-o mai mica masura de la nr_pat 0,58 .
Componenta 3 se identifica in aceasta faza cu indicatorul dens .
Dupa aplicarea tehnicii de rotatie Varimax - pentru gasirea unor rezultate mai concludente , se obtine tabelul Rotated Component Matrix , si in aceasta etapa componentele se cristalizeaza mult mai clar din punctul de vedere al informatiei recuperate si de la "cine" anume , astfel :
componenta 1 confirma , este un indicator de sinteza , preluand informatii de la majoritatea indicilor si anume : speranta de viata la femei si barbati , mortalitatea infantila , consumul de energie , telefoanele mobile si inflatia - practic este un indicator sintetic si daca privim din perspectiva analizei factorilor , in spatele acestei componente se afla dimensiunea economica a vietii omului cat si sansele sale de supravietuire , tocmai in acest mediu . Dar daca se ia in considerare si semnul acestor ponderi , se reliefeaza cateva aspecte - un indice mare mob sau energie inseamna si o valoare negativa insa pentru indicele inflatie , se poate traduce ca tehnologia reprezinta o modalitate de crestere economica ceea ce duce si la o inflatie mai redusa, asa se intampla spre exemplu si cu legatura dintre speranta de viata si mortalitatea infantila
componenta 2 confirma si ea , preluand foarte multa informatie de la stud 0,84 si intr-o mai mica masura de la nr_pat 0,59 . Asadar acesta ar putea fi un indicator mixt, dar care reflecta totusi dimensiunea "educatie" si mult mai redus "sanatate"
componenta 3 se identifica de data aceasta foarte clar cu indicele dens - densitatea populatiei , un indice care ar putea ascunde in spatele sau gradul de urbanizare din tarile supuse analizei .
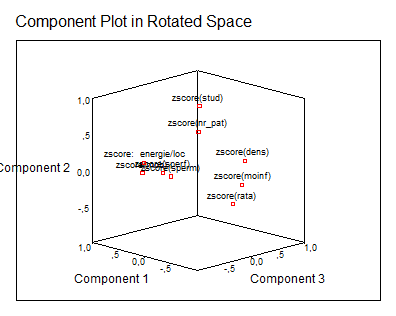
In figura alaturata , sunt reprezentate rezultatele anterioare si in spatiu , aceasta subliniaza apropierea dintre anumiti indici : energie , sperm/sperf , moinf si bineinteles componenta de care apartin .
Privind insa si coloanele rezultate qcl_1 , qcl_2 (a se consulta Anexe) - este realizata si o clasificare a tarilor , au rezultat de fapt numai 2 clustere :
Cluster 1 : Estonia , Letonia , Lituania , Ungaria , Polonia , Slovacia , Bulgaria, Romania
Cluster 2 : Belgia , Cehia , Danemarca , Germania , grecia , Spania , Franta , Irlanda , Italia , Cipru , Luxemburg , Malta ,Olanda , Austria , Portugalia , Slovenia , Finlanda , Suedia , Marea Britanie .
Asadar , este evidenta impartirea U.E. intre tarile cu vechime in aceasta structura - tari unde oamenii se pot astepta la o calitate a vietii mai ridicata si noile tari intrate, enumerate in cluster 1 , unde conform componentelor rezultate in urma ACP ; gasite pe coloanele fac1 , fac2 , fac3 ; se situeaza la un nivel inferior .
B. Tehnicile de clasificare
Algoritmul ierarhic
Intial se vor folosi algoritmii iararhici , utilizand cele 3 metode de agregare , dar vor fi prezentate numai cea bazata pe metoda cel mai departati vecini si cea pe baza centroizilor , cealalta neavand rezultate concludente in formarea unor clase in urma analizei .
A )In primul rand trebuie calculata matricea de proximitate , pe baza careia se vor forma clasele. In acest prim caz , se utilizeaza distanta euclidiana si rezulta tabelul de pe pagina urmatoare .
Fiecare element al matricei de proximitate reprezinta distanta dintre tari , distanta calculata in functie de toti cei 9 indicatori .
In urma aplicarii acestei tehnici de clasificare rezulta dendograma , in care se pot distinge cateva clase . De data aceasta exista o impartire si in cadrul acelui cluster rezultat la punctul anterior , cluster ce cuprindea tarile dezvoltate , cu vechime in U.E. Se formeaza astfel in mare clasa din 4 , 18 , 8,9 , 2,23,24 , o alta clasa 3,21,11,20,7,10,6,1 ,17,25 , a treia clasa : 15,22,13 ,5, 19 , mai sunt tarile 16 si 14 care nu reusesc sa se incadreze clar intr-o anumita clasa mai mare , si apoi 26 ,27 si 12 care formeaza clasa cea mai indepartata , clasa cu rezultatele cele mai slabe , unde calitatea vietii este mai scazuta - sunt trecute Romania ,Bulgaria si Letonia , asadar situatia se repeta , si privind tarile din primul cluster obtinut de asemenea se confirma . E clusterul ce contine tarile nordice , Germania , Franta - tarile cele mai dezvoltate , care ofera cel putin teoretic o viata mai buna , o surpriza este Marea Britanie care se afla abia in al doilea cluster ,alaturi de Italia, tari dezvoltate dar care nu ating toate aspectele luate in considerare in aceeasi masura , desi au o economie mai puternica decat a unor tari din primul pluton .
* * * * * * H I E R A R C H I C A L C L U S T E R A N A L Y S I S * * * * * *
Dendrogram using Complete Linkage
Rescaled Distance Cluster Combine
C A S E 0 5 10 15 20 25
Label Num +---------+---------+---------+---------+---------+
4
18
8
9
2
23
24
3
21
11
20
7
10
6
1
17
25
15
22
13
5
19
16
14
12
26
27

In tabelul de mai sus este prezentata modalitatea de agregare datelor in clustere . Spre exemplificare , la primul pas se ia in considerare distanta minima dintre toti indivizii , in cazul de fata 4 si 18 , adica Germania si Austria - tari clar cu aceleasi orientari si valori pe toate planurile , pe urmaroarea coloana la Coeffiecients este trecuta distanta calculata distanta euclidiana si apoi sunt trecute in coloanele imediat urmatoare clasele in care au mai aparut acesti indivizi , in acest caz fiind trecuta valoarea zero , asa cum este si normal , fiind primul pas . In ultima coloana , este inscris pasul la care se mai intalnesc indivizii respectivi, asadar la pasul 9 vom revedea cum 4 formeaza o clasa si cu 9 , rezultand 4,9,18 si algoritmul coninua pana sunt luati in considerare toti indivizii .
B ) Pentru cazul utilizarii metodei agregarii pe baza mediilor , va fi prezentata numai dendograma ,iar matricea de proximitate si tabelul in care este descris modul de formare a claselor se vor regasi in cadrul anexelor . De mentionat ca a fost utilizata distanta euclidiana patratica , fiind potivita acestui caz .
Asa cum se poate observa , reies clase asemanatoare din punctul de vedere al componentei , totusi analizand clasele mai indepartate se distinge 5,19,12,26 - un cluster alcatuit din tari cu rezultate mai slabe , dar spre deosebire de clusterul analog de la metoda precedenta Romania lipseste , si acelasi lucru se petrece si cu alte 2 tari Luxembourg si Malta - acesti indivizi formeaza fiecare cate o clasa de data aceasta , o trasatura comuna a acestora fiind chiar "extremul" , Romania are rezultatele cele mai slabe , iar Luxembourg este o tara foarte bogata dar foarte mica , ce presupune rezultate mai slabe din alte puncte de vedere .
* * * * * * H I E R A R C H I C A L C L U S T E R A N A L Y S I S * * * * * *
Dendrogram using Centroid Method
Rescaled Distance Cluster Combine
C A S E 0 5 10 15 20 25
Label Num +---------+---------+---------+---------+---------+
4
18
8
3
21
11
20
7
10
6
1
17
2
25
9
23
24
15
22
13
5
19
12
26
14
16
27
Mai departe vor fi supuse analizei si variabilele , adica tocmai aceste criterii , utilizand un algoritm ierarhic si anume metoda celor mai indepartati vecini . Matricea de proximitate este trecuta mai jos si a fost utilizata distanta euclidiana :
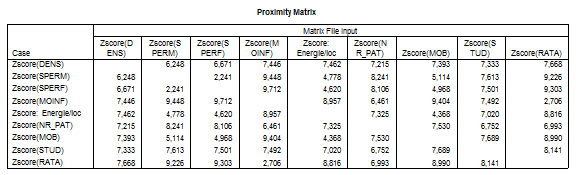
Modalitatea de formare a claselor este descrisa in tabelul urmator , coloana "Coefficients" avand trecute distantele dintre indivizi si este folositor tocmai pentru a intelege mai bine dendograma , unde clasele sunt vizibile si grafic .
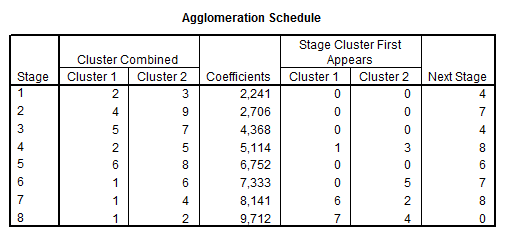
Privind si dendograma pot fi descrise urmatoarele clase :
- prima formata din speranta de viata pentru femei si barbati , cele 2 criterii fiind strans legate - distanta cea mai mica a fost gasita intre acestea doua .
- a doua clasa are in componenta mob si energie , asadar se constituie intr-un posibil indicator al industriei si servicilor pentru tarile analizate
- a treia clasa este formata din indicii moinf si rata
- ultima clasa este tot mixta , aici gasind nr_pat , stud si dens , clasa cea mai indepartata dar care aduna indici din domenii cheie : sanatatea , educatia si gradul de aglomerare a populatiei .
Este evident faptul ca au rezultat clase foarte diferite in comparatie cu ACP , in cadrul ACP fiind rezultate mult mai concludente .
* * * * * * H I E R A R C H I C A L C L U S T E R A N A L Y S I S * * * * * *
Dendrogram using Complete Linkage
Rescaled Distance Cluster Combine
C A S E 0 5 10 15 20 25
Label Num +---------+---------+---------+---------+---------+
ZSPERM 2
ZSPERF 3
ZEne 5
ZMOB 7
ZMOINF 4
ZRATA 9
ZNR_PAT 6
ZSTUD 8
ZDENS 1
Concluzii. In urma tehnicilor de analiza datelor aplicate, s-a reusit obtinerea unor indicatori care pot sintetiza mai bine informatia privind calitatea vietii ,exista astfel determinata componenta economica , demografica si educationala , in functie de care s-a putut obtine o prima clasificare intre tari , pe de o parte acele tari dezvoltate cu scoruri bune pe toate planurile , sau aproape toate si pe de alta parte tarile recent aderate la Uniunea Europeana , tari aflate in curs de dezvoltare care promit insa , nemaifiind pe ansamblu la distante foarte mari de scorurile medii din cadrul Uniunii . Totusi privind evolutia Romaniei , se poate spune ca in acest moment exista la nivelul acesteia rezultate mai slabe in general privind componenta economica dar cu progrese vizibile si rezultate apropiate de media europeana privind celelalte aspecte luate in considerare . Trebuie mentionat insa faptul ca aceste criterii prezinta cantitativ situatia , fiind mult mai greu de cuantificat calitatea economiei , a educatiei sau a altor aspecte din societate .
S-a putut realiza insa si o clasificare mai fina intre aceste tari , fiind sesizabile discrepante si in cadrul tarilor dezvoltate . Omul pare sa aiba sansa unei vieti mai bune nu neaparat in cadrul unei puteri economice pe plan mondial precum Italia sau Marea Britanie ci in cadrul unor tari mai mici , care apar cu rezultate notabile nu numai pe plan economic , tarile nordice fiind in acest caz alternativa .
ANEXE

Tabelul din stanga contine scorurile obtinute in cadrul ACP , de fiecare indice in urma aplicarii metodei de rotatie Varimax .
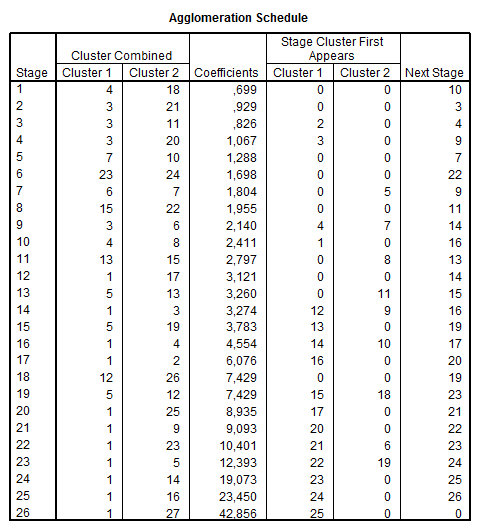
Tabelul contine formarea clusterelor pas cu pas - metoda pe baza agregarii mediilor .
Bibliografia
"Europe in figures - Eurostat yearbook " , editia 2006-2007 https://ec.europa.eu/eurostat
|
Politica de confidentialitate |
| Copyright ©
2026 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |