
Daca se considera ca a << b si ka << 1 (conditii pentru aproximatia unidimensionala), rezulta pentru cele doua componente ale densitatii curentului de suprafata urmatoarele valori:
![]() (4.39)
(4.39)
![]() (4.40)
(4.40)
Astfel curentul total si sarcina totala pe unitate de lungime sunt:
![]() (4.41)
(4.41)
![]() (4.42)
(4.42)
unde ![]() si
si ![]() sunt densitatea
curentului de suprafata, respectiv densitatea de sarcina.
sunt densitatea
curentului de suprafata, respectiv densitatea de sarcina.
Legea de conservare a sarcinii este incorporata in ecuatia de continuitate:
![]()
|
|
|
Fig. 4.12. Configuratia antenei bucla: a) bucla iluminata de un camp electric Ei(R) - privire spatiala; b) proiectiile vectorului camp in planul buclei. |
Pentru regim armonic:
![]()
Deoarece ![]() atunci, in coordonate
sferice,
atunci, in coordonate
sferice,
 ,
,
iar ecuatia de continuitate devine:
![]() (4.43)
(4.43)
Constanta de
propagare a mediului ![]() este considerata
in cele ce urmeaza, pentru antena care se afla in aer,
este considerata
in cele ce urmeaza, pentru antena care se afla in aer, ![]() si
si ![]() .
.
Pentru medii
conductoare, ![]() va fi inlocuit cu
va fi inlocuit cu ![]() ,
,
iar ![]() va fi inlocuit cu
va fi inlocuit cu ![]() .
.
Ecuatia
integrala pentru curentul ![]() poate fi
obtinuta de la conditia la limita pe suprafata buclei.
poate fi
obtinuta de la conditia la limita pe suprafata buclei.
Daca
consideram relatia de definire a potentialului scalar ![]() ,
,
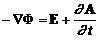 ,
,
pentru regim sinusoidal, pe suprafata buclei rezulta:
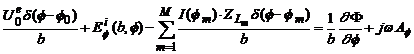 (4.44)
(4.44)
unde:
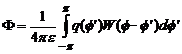 (4.45)
(4.45)
 (4.46)
(4.46)
 (4.47)
(4.47)
![]() (4.48)
(4.48)
R - distanta dintre punctele ![]() si
si ![]() .
.
Din relatia
(4.43) se determina ![]() :
:
![]()
Inlocuind ![]() in relatia
(4.45),
in relatia
(4.45),
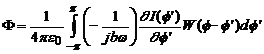

Daca se integreaza prin parti,
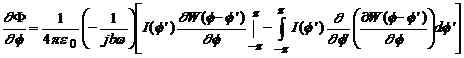
Deoarece ![]() si
si ![]() ,
,
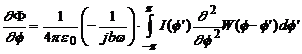

unde x este impedanta caracteristica a spatiului liber (§ 2.)
Ecuatia (4.44) devine:

Daca se
inlocuieste in membrul drept valoarea lui ![]() conform (4.46) si valoarea lui
conform (4.46) si valoarea lui ![]() ,se obtine:
,se obtine:

unde:
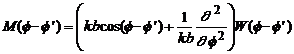 (4.50)
(4.50)
Miezul rezultat ![]() poate fi reprezentat
printr-o serie Fourier:
poate fi reprezentat
printr-o serie Fourier:
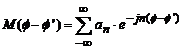 (4.51)
(4.51)
unde ![]() (4.52)
(4.52)
Nn -
provine din dezvoltarea in serie Fourier a primului miez ![]() :
:
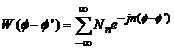 (4.53)
(4.53)
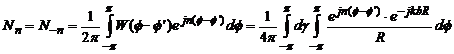 (4.54)
(4.54)
De asemenea curentul
![]() poate fi reprezentat
printr-o serie Fourier:
poate fi reprezentat
printr-o serie Fourier:
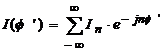 (4.55)
(4.55)
unde:
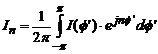 (4.56)
(4.56)
Daca se
inlocuieste in relatia (4.49) pe ![]() dat de (4.51) se
obtine:
dat de (4.51) se
obtine:

si conform relatiei (4.56) rezulta:
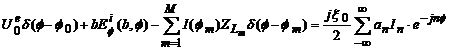 (4.57)
(4.57)
Din aceasta
ecuatie se pot calcula coeficientii ![]() si deci pe
si deci pe ![]() , daca se cunoaste
, daca se cunoaste ![]() si
si ![]() .
.
![]() se calculeaza cu
ajutorul lui (4.52), unde coeficienti
se calculeaza cu
ajutorul lui (4.52), unde coeficienti ![]() au fost determinati
in [Wu62]:
au fost determinati
in [Wu62]:
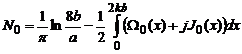 (4.58)
(4.58)
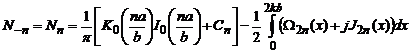 (4.59)
(4.59)
unde:
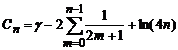 (4.60)
(4.60)
![]() este constanta lui
Euler
este constanta lui
Euler
![]() este functia
Bessel de speta a doua modificata
este functia
Bessel de speta a doua modificata
![]() este functia
Bessel de prima speta modificata
este functia
Bessel de prima speta modificata
![]() este functia
Bessel (de prima speta)
este functia
Bessel (de prima speta)
![]() este functia
Lommel Weber [Jahnker45], [Jahnker60]
este functia
Lommel Weber [Jahnker45], [Jahnker60]
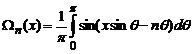 (4.61)
(4.61)
In cele ce urmeaza se presupune ca bucla este iluminata de o unda plana (Ei si Bi sunt perpendiculari unul pe altul si amandoi perpendiculari pe directia de propagare).
Vectorul camp electric poate fi reprezentat ca o unda progresiva in directia R.
![]() (4.62)
(4.62)
![]() este vectorul camp
electric la centrul buclei (R=0).
este vectorul camp
electric la centrul buclei (R=0).
Din Fig.4.1 se
observa ca vectorul camp electric incident la punctul (z = 0, b,![]() ) este:
) este:
![]() (4.63)
(4.63)
Dar ![]()
![]()
![]()
Asadar ,
![]() (4.64)
(4.64)
Pentru a determina
componenta ![]() a vectorului
a vectorului ![]() , adica
, adica ![]() , (deoarece numai aceasta componenta induce curent
in bucla), trebuie sa se ia numai componentele lui
, (deoarece numai aceasta componenta induce curent
in bucla), trebuie sa se ia numai componentele lui ![]() din planul xOy si
anume
din planul xOy si
anume ![]() si
si ![]() .
.
Componenta
tangentiala la bucla ![]() data de
data de ![]() satisface
relatia:
satisface
relatia:
 (4.65)
(4.65)
![]() (4.66)
(4.66)
Componenta
tangentiala la bucla ![]() , data de
, data de ![]() satisface
relatia:
satisface
relatia:
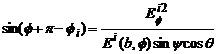 (4.67)
(4.67)
![]() (4.68)
(4.68)
Componenta
tangentiala la bucla a lui ![]() este:
este:
![]() =
=![]() -
- ![]() (4.69)
(4.69)
![]() (4.70)
(4.70)
sau
![]() =
=![]() (4.71)
(4.71)
![]() poate fi
reprezentata printr-o serie Fourier.
poate fi
reprezentata printr-o serie Fourier.![]()
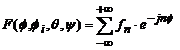 (4.72)
(4.72)
unde
coeficientii ![]() sunt:
sunt:
 (4.73)
(4.73)
Coeficientii ![]() pot fi calculati
astfel:
pot fi calculati
astfel:
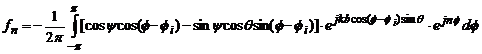 (4.74)
(4.74)
sau daca se
inmultesc ambii membri ai ecuatiei cu ![]() , atunci:
, atunci:
![]()

![]() (4.75)
(4.75)
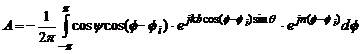
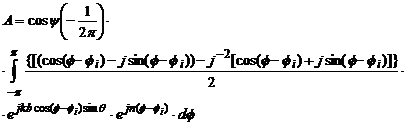
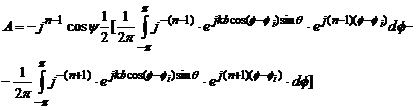
![]() (4.76)
(4.76)
unde ![]() este reprezentarea
integrala a functiei Bessel de prima speta si ordin
intreg.
este reprezentarea
integrala a functiei Bessel de prima speta si ordin
intreg.
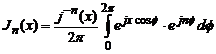 (4.77)
(4.77)

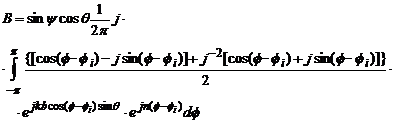
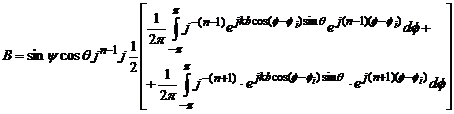
![]()
![]()
Deci
![]() (4.78)
(4.78)
Deoarece ![]() si
si
![]() , rezulta
ca:
, rezulta
ca:
![]() (4.79)
(4.79)
Daca se
descompune ![]() ,
, ![]() devine:
devine:
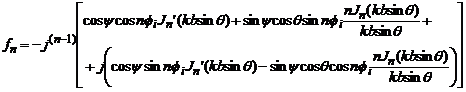 (4.80)
(4.80)
Pentru bucla
electric mica, kb < 1, se calculeaza doar ![]() :
:
![]()
![]() (4.81)
(4.81)
![]()
![]()
![]() (4.83)
(4.83)
Componenta
tangentiala a campului in punctul ![]() pe bucla
pe bucla ![]() este:
este:

![]()
Deoarece numai
componenta lui ![]() din planul buclei
induce curent, se iau urmatoarele unghiuri de incidenta:
din planul buclei
induce curent, se iau urmatoarele unghiuri de incidenta:
![]() (in acest caz,
(in acest caz, ![]() este perpendicular pe
planul buclei)
este perpendicular pe
planul buclei)
![]() (4.85)
(4.85)
![]() (4.86)
(4.86)
![]() (4.87)
(4.87)
In situatia
aceasta ![]() este maxim si nu
depinde de
este maxim si nu
depinde de ![]() , iar
, iar ![]() si
si ![]() depind de
depind de ![]() .
.
 (4.88)
(4.88)
Deci ![]() =max pentru
=max pentru ![]() =
= ![]() si
si
![]() (4.89)
(4.89)
Daca se revine
la ecuatia (4.57) si se inlocuieste ![]() conform (4.71) si
(4.72), se obtine:
conform (4.71) si
(4.72), se obtine:
 (4.90)
(4.90)
Inmultind ambii
membri ai ecuatiei (4.90) cu ![]() si apoi integrand
de la (
si apoi integrand
de la (![]() ) la
) la ![]() , rezulta:
, rezulta:
 (4.91)
(4.91)
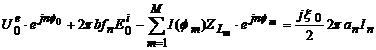 (4.92)
(4.92)
 (4.93)
(4.93)
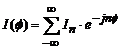 (4.94)
(4.94)
|
Politica de confidentialitate |
| Copyright ©
2026 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |