
Harti Karnaugh cu patru variabile
Folosindu-ne de codul Gray, putem construi harti Karnaugh mai mari. O harta Karnaugh cu patru variabile arata precum cea de mai jos:
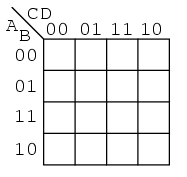
Exemplele de mai jos ilustreaza simplificarea expresiilor booleene ce sunt prea greu de realizat prin intermediul regulilor de simplificare booleana. Aceste expresii pot fi simplificate cu algebra booleana. Totusi, utilizarea hartilor Karnaugh este un procedeu mult mai rapid si mai usor, mai ales daca exista multe simplificari logice de realizat.
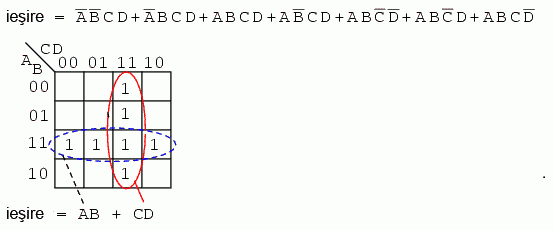
Expresia booleana de mai sus contine 7 produse. Acesti termeni sunt grupati de sus in jos si de la stanga la dreapta pe harta Karnaugh de mai sus. De exemplu, primul termen, A'B'CD, se regaseste pe randul 1, casuta a 3-a, si corespunde locatiei A = 0, B = 0, C = 1, D = 1. Ceilalti termeni sunt pozitionati intr-o maniera similara. Grupul orizontal (albastru) corespunde termenului AB, iar grupul vertical (rosu) corespunde expresiei booleene CD. Din moment ce avem doua grupuri, rezultatul trebuie sa fie o suma de doua produse, prin urmare, AB + CD.
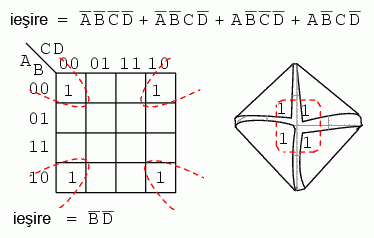
In cazul de mai sus, "impaturim" cele patru colturi ale hartii Karnaugh, precum un servetel, pentru a observa mai bine adiacenta celor patru regiuni. B = 0 si D = 0 pentru toate regiunile. Celelalte variabile, A si B, sunt 0 in unele cazuri si 1 in altele. Prin urmare, aceste variabile nu se vor regasi in rezultatul final al expresiei simplificate.
Pentru o vizualizare mai buna, ne putem imagina ca indoim marginile de jos si de sus a hartii sub forma unui cilindru. In acest caz, ambele grupuri sunt adiacente si formeaza practic un singur grup. Acest lucru ne spune ca rezultatul este un singur termen. Singura variabila comuna a acestui grup de 8 variabile este B = 0. Rezultatul simplificarii este prin urmare B'.
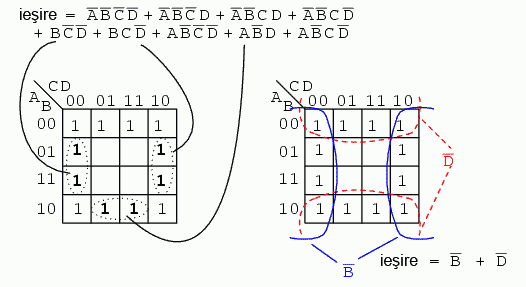
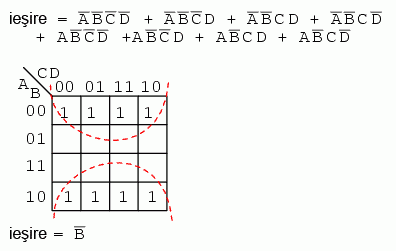
Expresia booleana de mai sus contine 9 termeni de produse, dintre care trei au doar trei variabile booleene in loc de patru. Diferenta consta in faptul ca, desi termenii ce contin patru variabile booleene acopera o singura regiune, termenii cu trei variabile booleene acopera o pereche de regiuni fiecare.
Trecand la simplificare, formam doua grupuri de cate opt termeni. Regiunile ce se regasesc in colt sunt comune ambelor grupuri. Acest lucru este corect. De fapt, aceasta strategie conduce la o solutie mai buna decat daca am fi format un grup de opt si un grup de patru regiuni, fara nicio regiune comuna celor doua. Solutia finala este B' + D'.

In exemplul de mai sus, trei regiuni formeaza doua grupuri de cate doua. O a patra regiune nu poate fi combinata cu nicio alta regiune, ceea ce se intampla frecvent in situatiile reale. In acest caz, termenul ABCD ramane neschimbat in cadrul procesului de simplificare a expresiei booleene initiale. Rezultatul este B'C'D' + A'B'D' + ABCD.
Adeseori, exista mai mult de o singura solutie cu cost minim pentru expresia nesimplificata. Un astfel de caz este cel de mai jos:
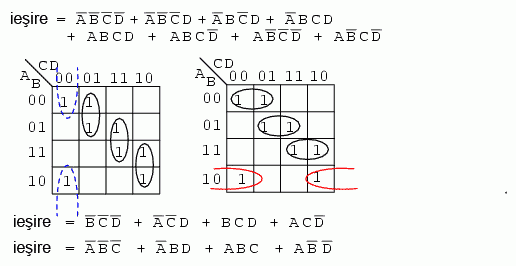
Ambele rezultate de mai sus contin patru termeni, cu trei variabile booleene fiecare. Ambele solutii sunt valide din punct de vedere al minimizarii costurilor. Diferenta dintre cele doua solutii finale consta in modul de grupare al regiunilor. Reamintim faptul ca o solutie cu cost minim este acea solutie ce permite o implementare fizica a circuitului logic cu un numar cat mai mic de porti logice si numar de intrari.
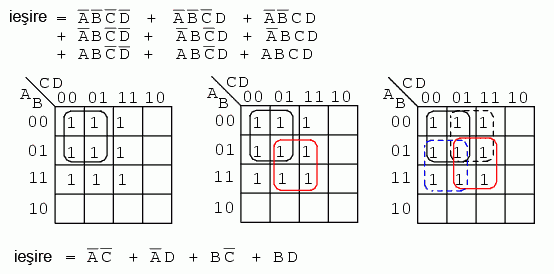
In urmatorul exemplu, cel de mai sus, dupa ce trecem toate valorile de 1 pe harta Karnaugh, realizam primul pas al simplificarii, si anume, gruparea primelor patru regiuni (stanga). In acest punct, s-ar putea sa nu fie foarte evident cum am putea grupa regiunile ramase.
La pasul al doilea (centru), grupam inca patru regiuni. Mai raman in acest moment inca doua regiuni negrupate. Solutia cu cost minim este sa grupam aceste doua regiuni, ca si grupuri de patru, conform figurii din dreapta.
Atentie, nu incercati sa realizati grupuri de cate trei. Gruparile trebuie sa fie sub forma puterilor lui 2, si anume, 1, 2, 4, 8, etc.

Avem din nou mai sus un exemplu ce suporta doua solutii cu cost minim. Formam initial cele doua grupuri de cate patru regiuni (rosu si albastru). Solutia finala depinde de modul in care grupam regiunea ramasa libera. Daca o introducem in grupul din stanga (rosu), solutia este ABC'. Daca o introducem in grupul din dreapta (albastru), solutia este ABD. Indiferent de alegerea facuta, ambele solutii sunt corecte din punct de vedere al minimizarii costurilor de implementare.

Mai sus este un exemplu de simplificare cu harti Karnaugh (stanga) precum si cu regulile algebrei booleene (dreapta). C' (C = 0) reprezinta aria formata de cele opt regiuni din stanga. Regiunea ramasa negrupata este echivalenta cu expresia ABCD. Grupand aceasta regiune cu cea din stanga ei, simplifica termenul ABCD la ABD. Rezultatul final este prin urmare C' + ABD.
Cazul de mai sus este un exemplu rar a unei probleme cu patru variabile ce poate fi redusa destul de usor si cu algebra booleana. Asta in cazul in care va amintiti teoremele de simplificare booleana.
|
Politica de confidentialitate |
| Copyright ©
2026 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |