
Puterea si cuplul electromagnetic ale masinii asincrone
Puterea electrica instantanee a masinii asincrone, in cazul general cand alimentarea are loc dinspre stator si dinspre rotor, se poate exprima astfel:
![]() . (2.78)
. (2.78)
In aceasta relatie, conform celor stabilite in subcapitolul 2.2, marimile rotorice, ca marimi scalare sunt raportate la stator iar ca marimi vectoriale sunt raportate la rotor. Acest procedeu nu modifica forma expresiei puterii instantanee. Expresia (2.78) se poate pune sub forma matriceala astfel [21]:
![]() . (2.79)
. (2.79)
In relatia (2.79) la marimile rotorice indicele semnifica faptul ca aceste marimi se refera la sistemul de axe trifazat solidar cu rotorul. Matricea [x]T este transpusa matricii [x] adica:
![]() . (2.80)
. (2.80)
Pentru exprimarea puterii instantanee cu ajutorul componentelor bifazate ortogonale se foloseste, atat pentru curenti cat si pentru tensiuni, relatia de recurenta (1.29). Se obtine astfel:
![]()
![]() (2.81)
(2.81)
Efectuand operatiile cu matricile [A] si [A]-1 (relatiile 1.31) se obtine matricea coeficientilor de putere trifazata:
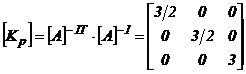 . (2.82)
. (2.82)
Efectuand
calculele, conform (2.81), prin introducerea matricilor ![]() si
si ![]() rezulta expresia
puterii instantanee sub forma:
rezulta expresia
puterii instantanee sub forma:
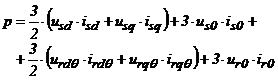 . (2.83)
. (2.83)
Expresia (2.83) se poate exprima si cu ajutorul fazorilor spatiali sub forma:
![]() . (2.84)
. (2.84)
Fazorii
spatiali us, is respectiv ur,
i r se refera la o faza. Pentru a lua in
considerare efectul celor trei faze, in relatia (2.84) apare factorul
trei. Deoarece se lucreaza cu marimi instantanee (in regim permanent
sinusoidal apare in mod obisnuit valoarea maxima ![]() si nu valoarea
efectiva U). Din aceasta
cauza apare factorul
si nu valoarea
efectiva U). Din aceasta
cauza apare factorul ![]() in relatia
puterii instantanee [21]. Fazorii spatiali din relatia (2.84) se vor
raporta la un sistem de axe comun, oarecare, (fig. 2.2).
Conform relatiei (1.36), unde:
in relatia
puterii instantanee [21]. Fazorii spatiali din relatia (2.84) se vor
raporta la un sistem de axe comun, oarecare, (fig. 2.2).
Conform relatiei (1.36), unde:
pentru fazorii statorici 1 = 0 si
pentru fazorii rotorici 1 = si
In cazul general se poate scrie:
![]() si
si ![]() . (2.85)
. (2.85)
Astfel produsele din (2.84) devin:
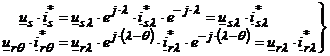 ;
;
Cu aceasta relatia (2.84) devine:
![]() . (2.87)
. (2.87)
In relatia (2.87) se inlocuiesc tensiunile us si ur cu expresiile (2.15) si respectiv (2.18) si tensiunile us0 si ur0 cu relatiile:
![]() ;
;
![]() .
.
Se
inlocuiesc de asemenea fluxurile cu relatiile (2.74) si (2.75).
Dezvoltand calculele si tinand seama ca, in general, ![]() , relatia (2.87) conduce la [21]:
, relatia (2.87) conduce la [21]:
 .
.
(2.88)
In dezvoltarea de mai sus termenul:
![]() .
.
deoarece
este pur imaginar. Acest termen contine ![]() , in functie de sistemul de axe la care se
raporteaza fazorii spatiali. Disparitia sa conduce la concluzia
ca - dupa cum este normal - expresiile diferitelor puteri sunt
independente de sistemul de axe d - q ales. Din
expresia puterii mecanice (rel. 2.88) se observa ca componentele
homopolare nu contribuie la producerea cuplului.
, in functie de sistemul de axe la care se
raporteaza fazorii spatiali. Disparitia sa conduce la concluzia
ca - dupa cum este normal - expresiile diferitelor puteri sunt
independente de sistemul de axe d - q ales. Din
expresia puterii mecanice (rel. 2.88) se observa ca componentele
homopolare nu contribuie la producerea cuplului.
Tinand seama de expresiile fluxurilor (2.74) si (2.75) puterea mecanica se poate pune si sub formele:
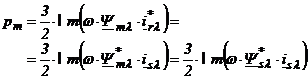 . (2.89)
. (2.89)
Cuplul electromagnetic me rezulta din expresia puterii mecanice care poate fi scrisa sub forma:
![]() ,
,
unde,
r este viteza
unghiulara a rotorului exprimata in grade mecanice, in timp ce este exprimata in grade
electrice. Deoarece ![]() rezulta:
rezulta:
![]() . (2.90)
. (2.90)
Din expresia puterii mecanice (2.88):
![]() , (2.91)
, (2.91)
si (2.89) rezulta cuplul electromagnetic instantaneu exprimat:
cu marimi statorice:
![]() ; (2.92)
; (2.92)
cu marimi rotorice:
![]() ; (2.93)
; (2.93)
cu curenti:
![]() ; (2.94)
; (2.94)
cu fluxul de magnetizare:
![]() ; (2.95)
; (2.95)
sau
![]() . (2.96)
. (2.96)
Expresia cuplului electromagnetic, ca si a puterii, este invariabila la transformarea sistemului de axe. Expresiile fazoriale ale cuplului electromagnetic sunt sintetizate in tabelul 2.1. [21].
|
Tabelul 2.1. Expresiile fazoriale ale cuplului electromagnetic |
||||||
|
is |
ir |
s |
r |
m |
Expresia cuplului |
|
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
● denota variabilele utilizate pentru calculul cuplului. |
||||||
Daca se considera relatia (1.14), din relatiile (2.92) -(2.96) se obtin expresiile cuplului - exprimate in functie de componentele bifazate ale marimilor care intervin - astfel:
cu marimi statorice:
![]() ; (2.97)
; (2.97)
cu marimi rotorice:
![]() ; (2.98)
; (2.98)
cu curenti:
![]() ; (2.99)
; (2.99)
cu fluxul de magnetizare:
![]() ; (2.100)
; (2.100)
sau
![]() . (2.101)
. (2.101)
Expresia cuplului electromagnetic se poate scrie si matriceal. Pentru aceasta, pe baza relatiei (1.20), din relatiile (2.97) - (2.101) rezulta cuplul in functie de:
marimile statorice:
![]() ;
;
marimile rotorice:
![]() ;
;
curenti:
![]() ;
;
fluxul de magnetizare:
![]() ;
;
sau
![]() ;
;
unde matricea [Q] este (a se vedea subcap. 2.1):
 .
.
Expresiile (2.92) - (2.96) pot fi puse sub forma de produse vectoriale. De exemplu relatia (2.92), dupa modelul din subcap. 1.4, poate fi scrisa sub forma:
![]() ,
,
unde modulul cuplului este:
![]() ,
,
fiind unghiul dintre fazorul de flux si fazorul de curent. s si is, fiind modulele fazorilor respectivi, nu depind de sistemul de axe si de aceea indicele a fost omis in relatia (2.108).
Din relatiile (2.97) - (2.101) se observa ca, daca sistemul de axe comun se orienteaza dupa una din marimile care anuleaza componenta q a acesteia din termenul al doilea, atunci se obtine cuplul maxim - asemanator masinii de curent continuu complet compensate - asa cum s-a stabilit deja in subcap. 1.4. Acesta este principiul de baza pentru sistemele cu orientare dupa camp ale masinilor de curent alternativ.
|
Politica de confidentialitate |
| Copyright ©
2026 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |