
Ranfortii sunt lucrari de constructii care se utilizeaza pentru consolidarea terasamentelor si versantilor care pot sa ajunga in faza de alunecare si la care suprafata de alunecare posibila este situata la o adancime de pana la 3,5 m de la suprafata.
Ranfortii sunt realizati din beton, iar saparea in terenul de fundare se poate realiza mecanizat. Realizarea sapaturilor se executa perpendicular pe frontul ce urmeaza a fi sustinut si prezinta avantajul de a nu periclita stabilitatea terasamentelor in timpul executiei sapaturii in terenul de fundare.
Ranfortii se pot realiza si in forma tipizata, caz in care ei sunt proiectati pentru a putea prelua presiuni maxime pe talpa de 4 daN/cm2 si sunt utilizati la sustinerea taluzurilor drumurilor sau la stabilizarea taluzurilor sau versantilor aferenti cailor de comunicatie terestre.
Din experienta acumulata pana in prezent a rezultat ca aceste lucrari sunt oportune numai pentru lucrari in rambleu si foarte rar in debleu.
Ranfortul este alcatuit din fundatie si elevatie. Pentru fundatie s-au adoptat urmatoarele valori ale adancimilor de sapare: 3,5 m, 4,5 m si 5,5 m corespunzatoare tipurilor de ranforti, mic, mijlociu si mare.
Elevatia are inaltimi cuprinse intre 1 si 2 m si pe ea sunt asezate elementele de sustinere ce transmit o impingere terenului de fundare. Elementele de sutinere pot fi fasii prefabricate de planseu, fasii prefabricate de poduri, bolti prefabricate, etc.
In functie de adancimea la care se afla planul de alunecare posibila se stabileste tipul de ranfort care trebuie utilizat, cu respectarea conditiei de realizare a unei incastrari de minimum 2,0 m sub planul de alunecare.
In figura 5.1 este prezentat un ranfort cu principalele elemente constructive :

Executia ranfortului este posibila in doua moduri care difera intre ele prin pozitia platformei de lucru a utilajului de sapat, si care poate fi amplasata in amonte sau in aval. In general este de preferat amplasarea in amonte. Amplasarea in aval prezinta avantajul ca se poate realiza o adancime de sapare mai mare, atunci cand planul de alunecare este mai profund, dar are dezavantajul ca accesul utilajului de sapare este mai dificil si se dezafecteaza o suprafata mai mare de teren.
In tabelul 5.1 sunt prezentate comparativ solutiile de sustinere cu zid de sprijin din casete prefabricate si cei cu ranforti executati mecanizat.
Baretele sunt elemente de constructie din beton armat, care au o rezistenta mare si care se folosesc ca si fundatii de adancime, sau ca elemente structurale pentru lucrari de consolidare in cazul alunecarilor de teren de profunzime, atunci cand suprafata de alunecare probabila se gaseste la adancime de 4-10m.
Din punct de vedere constructiv baretele se pot realiza in urmatoarele tipuri constructive :
Tabel 5.1.
Costurile pe tipuri de consoloidare
|
Nr.crt. |
Indicator |
Zid de sprijin din casete prefabricate |
Sustinere - consolidare cu ranforti |
Diferenta |
|
1. |
Ciment [kg] |
3160 |
2460 |
22 |
|
2. |
Otel [kg] |
85,2 |
40 |
55 |
|
3. |
Prefabricate [m3] |
2 |
0,3 |
85 |
|
4. |
Pret cost (an1989)[lei] |
13250 |
8690 |
34 |
barete cu capitel izolat, (fig 5.2), barete cu capitel cu elemente de legatura: bolti sau grinzi (fig 5.3); barete grupate intr-un modul, prin solidarizare cu o grinda (fig 5.4 ); barete grupate intr-un modul prin solidarizare cu un cadru spatial (fig 5.5).



Fiecare solutie are un domeniu de aplicare bine precizat in functie de adancimea posibila a planului de alunecare, caracteristicile geotehnice ale terenului de fundare si impingerea pamantului.

Cele mai alese tipuri de barete folosite in Romania sunt cele cu dimensiunile 2,60 x 0,8 si cu o adancime de fundare cuprinsa intre 10 si 12 m.
Ca si baretele, coloanele din beton armat sunt elemente de fundare si reprezinta elementele structurii de rezistenta ale lucrarilor de consolidare.
Ele se realizeaza printr-o forare tubata cu diametrul cuprins intre 0,8 si 2 m. In interiorul tubului se monteaza armatura si apoi este turnat betonul.
Terenurile in care se utilizeaza coloanele pot avea o alcatuire litologica diversa, cu infiltratii de apa si alternanta de roci slabe.
Fundarea coloanelor se face la 7-9 m sub nivelul planului de alunecare, ele avand marele avantaj al posibilitatii de realizare a unor adancimi de fundare mai mare decat la barete, fig. 12.6.
Din punct de vedere constructiv, lucrarile de sustinere cu coloane se pot realiza in urmatoarele variante:
a.) coloane distantate, solidarizate prin grinda de continuitate;
b.) coloane tangente (joantive), solidarizate prin grinda de continuitate;
c.) coloane dispuse intr-un cadru plan, realizand un ranfort;
d.) coloane dispuse tangent, intr-un perete descarcat prin coloane de ancoraj.
Calculul unui element fisat (bareta sau coloana ) se face luand in considerare interactiunea acestor elemente cu terenul de fundare.
Terenul de fundare este asimilat cu un mediu elastic fiind caracterizat printr-un coeficient de pat Cz, care variaza proportional cu adancimea z.
Cz = m . z ; [N / m3 ]; (5.1 )
unde : m - este coeficientul de proportionalitate al terenului de fundare, ( N / m4 ).
Coeficientul de pat Cz se determina pentru straturile de pamant pana la o adancime conventionala "hm" care nu trebuie sa depaseasca inaltimea h a elementului fisat:
hm = 3,5 d1 + 1,5 ![]() h ; (
5.2)
h ; (
5.2)
unde d1 - diametrul coloanei, sau latura sectiunii baretei
Daca pe adancimea hm se intalneste un singur tip de roca se va utiliza valoarea coeficientului de proportionalitate al rocii stabilita in functie de natura rocilor si dependenta acestuia de idicele de consistenta respectiv cifra porilor.
Aceste corelatii sunt redate in tabelele 5.2 si 5.3
Tabel 5.2.
Valoarea coeficientului de proportionalitate pentru roci argiloase
|
Tip de roca |
Indicele de consistenta |
Domeniul de consistenta |
Coeficientul de proportionalitate m x.103 [N/ m4] |
|
Argile |
1,5 |
Foarte tare |
10.000 |
|
1,25 |
Tare |
8.000 |
|
|
Argile prafoase |
1 |
Plastic vartos |
6.000 |
|
0,75 |
Plastic consistent |
5.000 |
|
|
Argile nisipoase |
0,5 |
Plastic moale |
4.000 |
|
0,25 |
Plastic curgator |
500 2000 |
 |
Tabel 5.3.
Valoarea coeficientului de proportionalitate pentru nisipuri
Tip de nisip |
Starea de indesare |
Indicele porilor "e" |
mx103 [N/m4] |
|
Nisip prafos |
Afanat Mediu indesat indesat |
0,8 |
1500 |
|
0,6 - 0,8 |
2000 - 4000 |
||
|
0,6 |
5000 |
||
|
Nisip fin |
Afanat Mediu indesat indesat |
0,75 |
3000 |
|
0,6 - 0,75 |
4000 - 6000 |
||
|
0,6 |
7500 |
||
|
Nisip mijlociu |
Afanat Mediu indesat indesat |
0,7 |
3000 |
|
0,55 - 0,7 |
4000 - 6000 |
||
|
0,55 |
7500 |
||
|
Nisip mare |
Afanat Mediu indesat indesat |
0,7 |
5000 |
|
0,55 - 0,7 |
6000 - 10000 |
||
|
0,55 |
13000 |
||
|
Nisip cu pietris |
Afanat Mediu indesat indesat |
0,7 |
7000 |
|
0,55 - 0,7 |
10000 - 20000 |
||
|
0,55 |
25000 |
Daca terenul de fundare este neomogen, alcatuit din doua sau mai multe tipuri de roci atunci se stabileste un coeficient de proportionalitate echivalent, astfel:
pentru doua tipuri de roci :
![]() ; (5.3.)
; (5.3.)
pentru trei tipuri de roci
 ; (5.4.)
; (5.4.)
unde, h3 = hm -(h1 + h2 )
Calculul baretelor si coloanelor in cazul rocilor neomogene efectuat cu ajutorul coeficientului de proportionalitate echivalent este acoperitor si nu este posibil sa apara probleme de instabilitate datorita subdimensionarii.
Determinarea latimii elementelor fisate (barete sau coloane)
La baretele si coloanele dispuse pe un singur rand latimea "bc" a baretelor si a coloanelor cu diametru egal sau mai mare de 0,8 m se determina cu relatia:
bc = d + 1 [m]; (5.5 )
in care: d - diametrul coloanei sau latimea baretei.
Pentru celelalte cazuri relatia de calcul devine:
bc = 1,5d + 0,5 [m]; (5.6)
Pentru a asigura o interactiune optima intre elementele fisate si terenul de fundare, (fig.5.7), este necesar sa se asigure o distanta minima intre axele elmentelor data de relatia:
a![]() d + 1,0 ; [m]; (5.7)
d + 1,0 ; [m]; (5.7)
La elementele fisate dispuse pe mai multe randuri trebuie sa se tina seama si de conlucrarea de ansamblu, prin luarea in considerare atat a distantei dintre elementele unui rand cat si a distantei dintre randuri prin introducerea unui coeficient de conlucrare K, ( fig 5.8 ).

In acest caz latimea devine:
bc = (d+1) . K; (5.8)
in care:
K=
![]() x
x![]() (5.9)
(5.9)
Unde:
b = 1, pentru elementele fisate dispuse pe un singur rand;
b = 0,6, pentru elementele fisate dispuse pe doua randuri;
b = 0,5 , pentru elementele fisate dispuse pe trei randuri;
L - distanta dintre elemente;
hp - adancimea de fundare si care este: hp < 6 m pentru d = 1 m si hp < 18 m pentru d = 5 m.

Pentru valori intermediare ale lui d, adincimea de fundare se determina cu relatia :
hp = 3 (d + 1); (5.10)
In cazul in care baretele sunt dispuse pe doua randuri si acestea se intrepatrund pe o lungime egala cu jumatate din latura lunga a baretei, (fig 5.9) distanta minima dintre aceste barete trebuie sa fie:
a![]() d + 2 [m]; (5.11)
d + 2 [m]; (5.11)

Distantele diferentiate dintre barete, in functie de pozitia lor, se stabilesc din conditia ca fortele ce se transmit prin frecare de peretii laterali ai baretelor masivului de pamant sa nu depaseasca rezistenta la forfecare a acestuia.
Determinarea rigiditatii baretelor si coloanelor
Modul de calcul a elementului fisat depinde de valoarea adancimii
reduse, de introducere in terenul de fundare a acestuia, care se noteaza
cu ![]() si care se
calculeaza cu relatia:
si care se
calculeaza cu relatia:
![]() = a . h ; (5.12.)
= a . h ; (5.12.)
in care:
 (5.13)
(5.13)
unde: a - coeficient de interactiune, element fisat - teren de fundare;
h - adancimea efectiva de fundare a elementului fisat ;
Eb - modulul de elasticitate al betonului armat;
I - momentul de inertie al sectiunii transversale;
bc - latimea de calcul a elementului fisat.
Daca h 2,5 elementul se considera infinit rigid si se aplica relatiile de calcul de la fundatiile incastrate.
Daca h >2,5 elementul se considera elastic, caz in care se aplica relatiile de calcul ale unui element incovoiat.
In tabelul 12.4 sunt redate valorile corespunzatoare conditiei
de element infinit rigid: ![]() 2,5.
2,5.
Modul de calcul al elmentelor fisate rigide
Stabilitatea elementelor incastrate in teren sub actiunea sarcinilor exterioare este asigurata de rezistenta la compresiune a rocilor care vin in contact cu elmentul fisat.
Daca asupra elementului fisat actioneaza forte orizontale (H), forte verticale (N), precum si un moment incovoietor (M), (figura 5.10), atunci elementul tinde sa se roteasca in jurul unui punct care se afla la o adancime zo de la suprafata terenului si care este actionat de urmatoarele tipuri de forte orizontale si verticale:
Tabel 5.4.
Valorile fisei pentru ![]() 2,5
2,5
|
Coeficient de proportionalitate |
h (barete 2,6 x 0,8) |
h (coloane d= 1,08 m) |
|
2000 |
15,8 |
8,6 |
|
3000 |
14,6 |
7,9 |
|
4000 |
13,7 |
7,6 |
|
6000 |
12,7 |
7 |
|
8000 |
12 |
6,6 |
V1 - reactiunea pe verticala creata de sol pe talpa elementului fisat;
P1 - reactiunea laterala a solului pe partea anterioara a elementului, in partea superioara a acestuia ;
P2 - reactiunea laterala pe partea posterioara a elementului, in partea inferioara a acestuia ;
T1 si T2 - forte de frecare pe fetele laterale ale elementului ;
T3 - forta de frecare pe talpa elementului.

Caracterul general al deplasarilor
elementelor incastrate si starea de tensiune din elemente, depind in mod
esential, de marimea fortelor exterioare la care acestea sunt
supuse. In functie de valoarea fortelor exterioare putem intalni trei
cazuri:
a.) Cand fortele exterioare sunt mici, (fig. 5.11) si reactiunea solului pe fetele laterale si pe talpa se situeaza in domeniul elastic, diagramele presiunii pe fetele laterale au forma curbilinie, iar diagrama de presiune pe talpa elementului este trapezoidala.
b.) Fortele exterioare cresc si se produc deformatii plastice in terenul de fundare. Presiunea creata atinge valoarea limita a rezistentei pamantului, iar diagrama presiunii pe talpa are forma triunghiulara, fig. 5.12.
c.) In cazul cand fortele exterioare cresc in continuare, deformatiile plastice cresc, iar reactiunea terenului de fundare pe fetele laterale atinge valoarea limita a acestuia, fig 5.13.
In cele trei cazuri s-a examinat situatia particulara cand centrul de rotatie al elementului, punctul D, se afla deasupra talpii elementului fisat.
Pozitia acestui centru determina schema de calcul si caracterul diagramelor de presiune ale terenului de fundare pe fetele elementului fisat.
Tinand seama de distributia starii de tensiune in terenul de fundare, calculele de stabilitate si determinarea starii de tensiune in elementele fisate incastrate in teren se poate realiza prin doua procedee:
cu luarea in considerare a comportamentului elastic al terenului de fundare;
pe baza solicitarilor limita, corespunzatoare starii limita de echilibru a terenului de fundare.



Intucat cea de-a doua metoda este foarte laborioasa, in practica s-au generalizat relatiile de calcul considerand ca terenul de fundare se comporta elastic. Se considera un mediu elastic de tip Winkler, cu neglijarea fortelor de frecare intre elementul fisat si terenul de fundare, fig.5.14.

Consideram ca sub actiunea unei forte orizontale H, la o adancime Z, deplasarea orizontala a elementului se determina cu relatia:
Y
=( Z0 - Z ) tg![]() .; (5.14)
.; (5.14)
Tensiunea verticala a terenului sz este, conform ipotezei lui Winkler, direct proportionala cu aceasta deplasare :
sz = Cz ; y = C z ( z0 - z )tg q/ h; (5.15)
unde Cz = m . z si C = m . h sunt coeficientii de pat ai terenului de fundare la adancimile z si h.
Tensiunea maxima pe suprafata talpii se determina cu relatia:
smax = C dmax
= ![]() tga (5.16.)
tga (5.16.)
in care: C - coeficientul de pat la adancimea h;
a - latura elementului paralela cu directia fortei orizontale H;
dmax - tasarea maxima la extremitatea elementului fisat.
Necunoscutele Z0 si q se determina din conditile de echilibru:
S y = 0 si S M =0 ; (5.17)
 (5.18)
(5.18)
Din rezolvarea sistemului se obtin cele doua necunoscute :

unde:
![]()
Wt - modulul de rezistenta al talpii elementului fisat;
H - rezultanta fortelor orizontale exterioare;
l = ![]() - distanta de la
rezultanta fortelor exterioare orizontale pana la talpa
fundatiei;
- distanta de la
rezultanta fortelor exterioare orizontale pana la talpa
fundatiei;
M - momentul total al fortelor orizontale exterioare in raport cu talpa;
b - raportul coeficientilor de pat si reprezinta raportul de deformabilitate al terenului situat deasupra talpii fundatiei si cel situat sub talpa fundatiei;
![]()
C - coeficientul de pat al terenului aflat sub talpa fundatiei:
C = 3 x 105 KN/m3 pentru src = 1 MPa
C = 15 x 106 KN/m3 pentru src 25 MPa.
Pentru valori intermediare ale rezistentei la compresiune, coeficientul de pat se determina prin interpolare.
Calculul elementului fisat rigid
Calculul elementului fisat rigid urmareste determinarea eforturilor unitare si a deplasarilor suportate si incepe cu determinarea presiunilor orizontale pe cele doua fete verticale ale acestuia.
La adancimea z de la suprafata, perpendicular pe planul de actiune al fortelor orizontale, se dezvolta tensiuni orizontale a caror valoare se determina cu relatia :
sz = ; (
5.21 )
; (
5.21 )
In cazul elementelor fisate rigide pentru care ![]() = a h 2,5, verificarea
acestor eforturi unitare transmise de element asupra terenului de fundare se
efectueaza pentru adancimile: z = h/3 si z = h. La aceste adancimi
presiunile orizontale nu trebuie sa depaseasca presiunile
orizontale admisibile ale terenului de fundare, presiuni date de expresia:
= a h 2,5, verificarea
acestor eforturi unitare transmise de element asupra terenului de fundare se
efectueaza pentru adancimile: z = h/3 si z = h. La aceste adancimi
presiunile orizontale nu trebuie sa depaseasca presiunile
orizontale admisibile ale terenului de fundare, presiuni date de expresia:
Padm
= h![]() ( ga
.z. . tgj +
C) ; (5.22)
( ga
.z. . tgj +
C) ; (5.22)
In care: j - unghiul de frecare interioara;
C - coeziunea, care se considera 50 % - 60 % din valoarea indicata de STAS;
h - coeficient al conditiilor de lucru.
In cazul in care solul este neomogen, fiind alcatuit din mai multe straturi, valorile lui ga j si C se considera ca o medie ponderata pentru adancimea considerata.
Valoarea coeficientilor conditiilor de lucru h este data de relatia 5.23.
 (5.23)
(5.23)
unde: Hp - forte orizontale rezultate din incarcari permanente;
Ht - forte orizontale din incarcari temporare (Ht= 20 - 30 % Hp).
In aceste conditii pentru h se accepta o valoare h= 0,4-0,47.
De asemeni, f variaza intre 100-250, iar cos f intre 0,9-0,98 ; iar cu aceste valori medii rezulta ca valoarea raportului h/cosf este de 0,5.
Introducand aceste valori in relatia presiunii admisibile se obtine:
Padm = 2(ga z tgf +C)
Verificarea stabilitatii elementului fisat se determina din satisfacerea conditiei:
sz Padm, respectiv :
![]() z(z0 - z ) 2 (gaz tg j + C ).
z(z0 - z ) 2 (gaz tg j + C ).
2.Determinarea presiunilor verticale pe talpa elementului.
Pe talpa elementului fisat actioneaza tensiunile:
smax/min =![]()
![]() (5.24)
(5.24)
unde: a - latura elmentului fisat paralela cu forta orizontala H
A - sectiunea talpii elementului fisat
N - incarcarea axiala la nivelul talpii si care este data de expresia:
N=N0 + G - Ff. (5.25)
unde : N0 - incarcarea axiala la capul elementului fisat
G - greutatea proprie a elementului fisat
Ff - forta de frecare pe surafata laterala care se determina cu expresia:
Ff = K .P S f . l. (5.26)
in care : K - 0,5 pentru pamanturi necoezive
K - 0,6 pentru pamanturile coezive
P - perimetrul elementului fisat
f - rezistenta de calcul pe suprafata laterala a elementului. Valoarea coeficientului f functie de natura rocilor este data in tabelul 5.5, exprimata in kN/m2.
l - lungimea elementului in contact cu roca.
La utilizarea baretelor si coloanelor ca si lucrari de consolidare a solurilor instabile, incarcarea axiala este redusa si verificarea presiunilor pe talpa nu este necesara.
Tabel 5.5
Rezistenta la frecare f functie de natura rocilor
|
Adancimea medie a stratului [m] |
Pamanturi necoezive |
Pimanturi coezive |
|||||||
|
Mari |
Fine |
Prafoase |
0,8 |
0,7 |
0,6 |
0,5 |
0,4 |
0,3 |
|
|
1 |
35 |
23 |
10 |
35 |
23 |
15 |
12 |
5 |
2 |
|
2 |
42 |
30 |
15 |
42 |
30 |
20 |
17 |
7 |
3 |
|
3 |
48 |
35 |
25 |
48 |
35 |
25 |
20 |
8 |
4 |
|
4 |
53 |
38 |
27 |
53 |
38 |
27 |
22 |
9 |
5 |
|
5 |
56 |
40 |
29 |
56 |
40 |
29 |
24 |
10 |
6 |
|
7 |
60 |
43 |
32 |
60 |
43 |
32 |
25 |
11 |
7 |
|
10 |
65 |
46 |
34 |
65 |
46 |
34 |
26 |
12 |
8 |
|
15 |
72 |
51 |
38 |
72 |
51 |
38 |
28 |
14 |
10 |
|
20 |
79 |
56 |
41 |
79 |
56 |
41 |
30 |
16 |
12 |
In elementul fisat la adancimea z momentele incovoietoare se determina cu o relatie de tipul:
Mz
=H![]()
 (5.27)
(5.27)
Deplasarea orizontala la capatul elementului se poate determina cu relatia:
d w (z0 . K1 + l . K2 ) + d0 ( 5.28)
in care: l - lungimea libera a elementului deasupra suprafetei de incastrare;
d0 - deplasarea orizontala a elementului pe lungimea neincastrata;
K1 si K2 - coeficienti ce tin seama de rigiditatea elementului. Acesti coeficienti sunt redati in tabelul 5.6.
w - unghiul de rotire al elementului si care se poate determina cu relatiile:
w = 6H/S.m.h,
in cazul actiunii fortei orizontale H, cu bratul l, si
w =2bM / B.m.h
in cazul in care actioneaza numai momentul M; (H = 0).
Tabel 5.6.
Valorile coeficientilor de rigiditate K1 si K2
|
A x h |
Coeficientul |
l/h =1 |
l/h = 2 |
l/h =3 |
l/h = |
|
1,6 |
K1 |
1,0 |
1,0 |
1,0 |
1,0 |
|
K2 |
1,0 |
1,1 |
1,1 |
1,1 |
|
|
1,8 |
K1 |
1,0 |
1,1 |
1,1 |
1,1 |
|
K2 |
1,1 |
1,2 |
1,2 |
1,2 |
|
|
2,0 |
K1 |
1,1 |
1,1 |
1,1 |
1,2 |
|
K2 |
1,2 |
1,3 |
1,4 |
1,4 |
|
|
2,2 |
K1 |
1,1 |
1,2 |
1,2 |
1,2 |
|
K2 |
1,2 |
45 |
1,6 |
1,7 |
|
|
2,4 |
K1 |
1,1 |
1,2 |
1,3 |
1,3 |
|
K2 |
1,3 |
1,8 |
1,9 |
2,0 |
|
|
2,5 |
K1 |
1,2 |
1,3 |
1,4 |
1,4 |
|
K2 |
1,4 |
1,9 |
2,1 |
2,3 |
Calculul elementelor fisate, incastrate in teren stabil se va face luand in considerare presiunile laterale efective s care trebuie sa fie mai mici decat presiunea admisibila Padm , a terenului. Calculul se face pentru adancimea: z = h/3; s Padm
Padm
=h![]() (5.29)
(5.29)
s=![]() . z( zo-z) ; S=
. z( zo-z) ; S=![]() ; (5.30)
; (5.30)
in care :
b - raportul coeficientilor de proportionalitate m pe fetele laterale si talpa baretei ; pentru teren omogen b =1;
bc - latimea de calcul a baretei bc = d + 1;
d - grosimea baretei;
Wt - modulul de rezistenta al sectiunii transversale a baretei;
l = h1 + h adancimea baretei de sub radier si pana la talpa;
h1 - adancimea baretei deasupra planului de alunecare probabila;
h - adancimea de incastrare a baretei in teren stabil;
h - coeficientul conditiilor de lucru;
zo - adancimea punctului de rotatie. Se poate considera zo =0,7h.
Facand inlocuirile si punand conditiile la limita in relatia : s Padm se obtine ecuatia:
h= (5.31)
(5.31)
unde: n coeficient de conlucrare bareta - teren si care tine seama de pozitia in plan a baretelor (fig 5.15).

Daca in relatia 12.31 se fac notatiile:
b
= ![]() si c =
si c =![]() , atunci relatia 12.31 se poate scrie:
, atunci relatia 12.31 se poate scrie:
h2 - bh - c = 0 (5.32)
iar adancimea de incastrare se va considera solutia pozitiva a ecuatiei de gradul doi, data de relatia 12.33:
h=
![]() ; (5.33)
; (5.33)
Un element fisat este flexibil, daca adancimea redusa de penetrare in pamant este:
h2 = ah > 2,5 (5.34)
in care : h - adancimea efectiva de introducere in teren;
a - caracteristica de interactiune sol-element fisat.
a= (5.35)
(5.35)

Schemele de calcul ale solutiilor
constructive sunt prezentate in figura 5.16.
Calculul elementelor fisate urmareste determinarea eforturilor unitare si a deformatiilor suferite de acestea.
Deplasarea orizontala si rotirea sectiunii la nivelul solului se pot determina cu relatiile:
yo =H0 . dHH + M0 . dHM
fo = H0 . dMH + M0 . dMM (5.36)
in care : H0 si M0 sunt valorile fortei orizontale si a momentului incovoietor la nivelul suprafetei solului.
dHH - deplasarea orizontala a capului elementului sub actiunea unei forte orizontale unitare, H = 1 KN;
dHM - deplasarea orizontala a capului elementului sub actiunea unui moment incovoietor unitar M = 1 KN . m;
dMH - rotirea capului elementului sub actiunea unei forte unitare;
dMM - rotirea capului elementului sub actiunea unui moment unitar.
Deplasarile si rotirile elementului corespunzatoare solicitarilor unitare sunt redate in figura 5.17.

Aceste deformatii se calculeaza cu expresiile:
dHH =![]() (5.37)
(5.37)
![]() (5.38)
(5.38)
![]() (5.39)
(5.39)
in care: Eb - modulul de elasticitate al betonului
I - momentul de inertie al elementului fisat
a - coeficientul de interactiune element fisat - sol;
A0, B0, C0 - coeficienti adimensionali functie de natura terenului de fundare. Acesti coeficienti sunt redati in tabelul 5.7.
Tabel 5.7.
Valoarea coeficientilor A0, B0, C0
|
Adancime [m] |
Incastrare in roci necoezive |
Incastrare in roci stancoase |
||||
|
A0 |
B0 |
C0 |
A0 |
B0 |
C0 |
|
|
2,0 |
4,737 |
3,418 |
3,213 |
3,381 |
2,081 |
1,894 |
|
2,2 |
4,032 |
2,756 |
2,59 |
2,977 |
1,819 |
1,758 |
|
2,4 |
3,526 |
2,327 |
2,227 |
2,713 |
1,673 |
1,701 |
|
2,6 |
3,163 |
2,048 |
2,012 |
2,548 |
1,6 |
1,687 |
|
2,8 |
2,905 |
1,869 |
1,889 |
2,453 |
1,572 |
1,693 |
|
3,0 |
2,727 |
1,758 |
1,818 |
2,406 |
1,560 |
1,707 |
|
3,5 |
2,502 |
1,641 |
1,757 |
2,384 |
1,537 |
1,739 |
|
4,0 |
2,441 |
1,621 |
1,751 |
2,419 |
1,518 |
1,75 |
La adancimea z, pe fetele laterale se dezvolta presiuni orizontale, a caror marime este direct proportionala cu deplasarea orizontala si cu coeficientul de pat al terenului (Cz).
sz =Cz . yz = m . z . yz (5.40)
Verificarea presiunii se va face pentru
adancimea redusa ![]() = az si se va obtine urmatoarea presiune
laterala:
= az si se va obtine urmatoarea presiune
laterala:
s = m 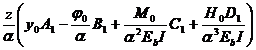 (5.41)
(5.41)
in care: A1, B1, C1, D1 - coeficienti functie de adancimea redusa. Acesti coeficienti sunt redati in tabelul 5.8.
Verificarea consta in indeplinirea conditiei:
sz Padm (5.42)
Padm
=2![]() (5.43)
(5.43)
Pentru elementele fisate incastrate in roci necoezive, trebuie sa se realizeze verificarea pentru adancimea z =0,85/a
In diferite sectiuni ale elementului fisat flexibil, la adancimea z, actioneaza momente incovoietoare, care se pot determina cu expresia:
Mz=a2EbIyoA3
- aEbIj0B3 + M0C3
+ ![]() (5.44)
(5.44)
A3, B3, C3, D3 coeficienti adimensionali functie de adancimea redusa z. Acesti coeficienti sunt redati in tabelul 5.8.
In cazul elementelor fisate cu adancimea redusa ![]() 2,5 care se reazema pe roci neconsolidate,
sau a celor cu adancimea redusa
2,5 care se reazema pe roci neconsolidate,
sau a celor cu adancimea redusa ![]() 4 care se reazama pe roci stancoase, momentul
maxim incovoietor care actioneaza in elementul fisat se poate
determina aproximativ cu relatia:
4 care se reazama pe roci stancoase, momentul
maxim incovoietor care actioneaza in elementul fisat se poate
determina aproximativ cu relatia:
Mmax
= M + H![]() ; (5.45)
; (5.45)
K2 - coeficient functie de marimile a si h (tabel 5.9.) si coeficientul h dat de relatia 5.46,:
![]() ; (5.46)
; (5.46)
Cz - coeficientul de pat al terenului de sub elementul fisat:
Cz = m . zo/0,2 hm
Io - momentul de inertie la baza elementului fisat ;
zo - parametru : zo = 10 m pentru h 10 m si zo = h cand h > 10 m.
hm - adancimea conventionala medie : hm = (3,5 di + 1,5)
di - diametrul coloanei sau elementului fisat
Tabel 5.8.
Valorile coeficientilor A1, B1, C1, D1 si A3, B3, C3, D3
|
Adancime redusa [m] |
Coeficienti |
|||||||
|
A1 |
B1 |
C1 |
D1 |
A3 |
B3 |
C3 |
D3 |
|
|
0,1 |
1 |
0,1 |
0,005 |
0 |
0 |
0 |
1 |
0,1 |
|
0,2 |
1 |
0,2 |
0,02 |
0,001 |
-0,001 |
0 |
1 |
0,2 |
|
0,3 |
1 |
0,3 |
0,045 |
0,005 |
-0,005 |
-0,001 |
1 |
0,3 |
|
0,4 |
1 |
0,4 |
0,08 |
0,011 |
-0,011 |
-0,002 |
1 |
0,4 |
|
0,5 |
1 |
0,5 |
0,125 |
0,021 |
-0,021 |
-0,005 |
0,999 |
0,5 |
|
0,6 |
0,999 |
0,6 |
0,18 |
0,036 |
-0,036 |
-0,011 |
0,998 |
0,6 |
|
0,7 |
0,999 |
0,7 |
0,245 |
0,057 |
-0,057 |
-0,02 |
0,996 |
0,699 |
|
0,8 |
0,997 |
0,799 |
0,32 |
0,085 |
-0,085 |
-0,034 |
0,992 |
0,799 |
|
0,9 |
0,995 |
0,899 |
0,405 |
0,121 |
-0,121 |
-0,055 |
0,985 |
0,897 |
|
1,0 |
0,992 |
0,997 |
0,499 |
0,167 |
-0,167 |
-0,083 |
0,975 |
0,994 |
|
1,1 |
0,987 |
1,095 |
0,604 |
0,222 |
-0,222 |
-0,122 |
0,96 |
1,09 |
|
1,2 |
0,979 |
1,192 |
0,718 |
0,288 |
-0,287 |
-0,173 |
0,938 |
1,183 |
|
1,3 |
0,969 |
1,287 |
0,814 |
0,365 |
-0,365 |
-0,238 |
0,907 |
1,273 |
|
1,4 |
0,955 |
1,379 |
0,974 |
0,456 |
-0,455 |
-0,319 |
0,866 |
1,358 |
|
1,5 |
0,937 |
1,468 |
1,115 |
0,56 |
-0,559 |
-0,42 |
0,811 |
1,437 |
|
1,6 |
0,913 |
1,553 |
1,264 |
0,678 |
-0,676 |
-0,543 |
0,739 |
1,507 |
|
1,7 |
0,882 |
1,663 |
1,421 |
0,812 |
-0,808 |
-0,691 |
0,646 |
1,566 |
|
1,8 |
0,843 |
1,706 |
1,584 |
0,961 |
-0,956 |
-0,867 |
0,53 |
1,612 |
|
1,9 |
0,795 |
1,37 |
1,752 |
1,126 |
-1,118 |
-1,074 |
0,385 |
1,64 |
|
2,0 |
0,735 |
1,823 |
1,924 |
1,308 |
-1,295 |
-1,814 |
0,207 |
1,646 |
|
2,2 |
0,575 |
1,887 |
2,272 |
1,72 |
-1,693 |
-1,906 |
-0,271 |
1,575 |
|
2,4 |
0,347 |
1,874 |
2,609 |
2,195 |
-2,141 |
-2,663 |
-0,949 |
1,392 |
|
2,8 |
-0,385 |
1,49 |
3,128 |
3,288 |
-3,103 |
-4,718 |
-3,108 |
-0,197 |
|
3,0 |
-0,928 |
1,037 |
3,225 |
3,858 |
-3,541 |
-6 |
-4,688 |
-0,894 |
|
3,5 |
-2,928 |
-1,272 |
2,463 |
4,98 |
-3,919 |
-9,544 |
-10,34 |
-5,854 |
|
4 |
-5,853 |
-5,941 |
-0,927 |
4,548 |
-1,614 |
-11,731 |
-17,731 |
-15,076 |
Tabel 5.9.
Valoarea coeficientului K2
|
Coeficient de interactiune sol-element, a |
Adancimea redusa h [m] |
||
|
h >3,5 |
h = 3 |
2,5 < h < 3 |
|
|
0,100 |
0,75 |
0,7 |
0,67 |
|
0,125 |
0,75 |
0,7 |
0,67 |
|
0,15 |
0,75 |
0,7 |
0,66 |
|
0,175 |
0,75 |
0,7 |
0,65 |
|
0,200 |
0,75 |
0,7 |
0,65 |
Calculul adancimii de incastrare a elementelor flexibile difera de cel pentru elementele fisate rigide, deoarece datele experimentale au scos in evidenta faptul ca neluarea in considerare a elasticitatii duce la o supradimensionare a adancimii de incastrare.

Pornind
de la distributia presiunilor se poate scrie ecuatia de echilibru a
fortelor ce actioneaza pe coloana, luand momentul acestora
in raport cu punctul in care diagrama presiunilor isi schimba semnul
(fig.5.18) distanta zo fata de suprafata.
Partea superioara a diagramei presiunilor se considera de forma parabolica, iar partea inferioara de forma triunghiulara.
In acest caz, ecuatia de momente devine:
![]() ; (5.47)
; (5.47)
Pentru o coloana cu d = 1,08 m vom avea;
Ps = Pi = Padm ; zo = 0,7 h ; bc = 2,08 m
Si ecuatia presiunii admisibile va fi:
Padm . h2 - 1,7 H . h - 2,35 H . h1 = 0 (5.48)
Necunoscuta din aceasta ecuatie este h - adancimea de incastrare. Daca h1 0, adancimea de incastrare va fi data de relatia:
 ; (5.49)
; (5.49)
Daca h1 = 0, adancimea de incastrare se determina cu expresia :
![]() ; (5.50)
; (5.50)
Armarea elementelor fisate se efectueaza pe intreaga adancime a acestora, cu ajutorul unor carcase formate din bare longitudinale, etrieri, bare sau inele rigidizate, carlige de manipulare.
Armaturile trebuie sa aiba urmatoarele dimensiuni minime :
armatura longitudinala f 14 OB 37 sau f 12 PC 52
etrieri f 10 OB 37 ;
carlige de manipulare f 18 OB 37.
Modul de armare al elementelor fisate este redat in figura 5.19.

Distanta minima dintre armaturile longitudinale se adopta 15 cm la bare si 5 cm la odgoane, iar grosimea de acoperire cu beton se adopta de minim 7 cm, iar la terenuri de fundare agresive 10 cm.
Betonul utilizat va fi B200 pentru barete si B300 pentru coloane.
Aria armaturilor se determina conform relatiei:
![]() ; (5.51)
; (5.51)
Ra, Rc - rezistenta de calcul a armaturii, respectiv a betonului;
Ab - aria betonului;
a - coeficient fizic de armare.
La armarea baretelor, care au un moment de inertie de circa 17 ori mai mare decat al coloanelor, la acestea se va utiliza un procent minim de armare. Acesta va fi de 25 kg armatura pe metru cub de beton.
Capetele superioare ale elementelor fisate se incastreaza intr-un radier sau rigla, iar dimensionarea acestora se face tinand cont de urmatoarele elemente:
corpul elementului fisat va patrunde in radier pe o lungime minima de 15 cm, fara betonul de egalizare;
distanta dintre fata elementului fisat si marginea radierului va fi de aproximativ 25 cm;
acoperirea cu beton a armaturii inferioare a radierului va fi de 15 cm, iar marca minima a betonului B-150.
In cazul in care elementele fisate sunt amplasate pe un singur rand, este indicata unirea capetelor acestora cu o grinda de continuizare care asigura o mai buna transmitere a impingerii pamanturilor asupra elementelor si o redistribuire a incarcarilor intre elemente, atat in cazul neuniformitatii impingerii pamantului, cat si in cazul neuniformitatii conlucrarii elementului fisat cu terenul de fundare.
Calculul elementelor fisate se realizeaza ca pentru o grinda continua pe mai multe reazeme, facandu-se chiar ipoteza ca unul dintre reazeme lipseste, fig.5.20.

Momentele incovoietoare se pot calcula cu relatii cunoscute de forma relatiilor de mai jos, grinda rezemata pe reazeme (12.52) si grinda in camp (12.53):
![]() ; (5.52)
; (5.52)
![]() ; (5.53)
; (5.53)
|
Politica de confidentialitate |
| Copyright ©
2026 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |