
CALCULUL ELEMENTELOR DE BETON ARMAT LA STAREA LIMITA DE DEFORMATII
Calculul la starea limita de deformatii consta in verificarea, sub incarcarile de exploatare, a valorii sagetii f < fadm sau a unei parti a acesteia Df Dfadm , astfel ca sa nu depaseasca valorile admise in raport cu destinatia elementelor, conform conditiilor din tabelul 1.
Tabelul 1
Conditiile de verificare la starea limita de deformatii
|
Tipul de element |
Relatia de verificare |
Denumirea elementelor structurale |
Limite admise[1] |
|
Elemente componente ale planseelor |
|
Plansee care sustin sau sunt atasate unor elemente nestructurale care pot fi deteriorate de deformatiile mari ale planseelor |
|
|
Plansee care nu sustin sau nu sunt atasate unor elemente nestructurale care pot fi deteriorate de deformatiile mari ale planseelor |
|
||
|
|
Planseele salilor de spectacole, inclusiv cele ale balcoanelor acestora; gradenele tribunelor |
|
|
|
Grinzi de rulare |
|
Poduri rulante manuale Poduri rulante electrice |
|
Nota: Incarcarile permanente se iau in considerare cu intensitati normate, iar cele variabile cu intensitatile normate afectate cu coeficientul nd.
Semnificatia termenilor din tabelul 12 este urmatoarea:
![]() este sageata de
lunga durata din incarcarea totala de exploatare (cu luarea
in considerare a deformatiilor in timp);
este sageata de
lunga durata din incarcarea totala de exploatare (cu luarea
in considerare a deformatiilor in timp);
![]() sageata
de scurta durata din incarcarea de exploatare care
actioneaza inainte de executarea elementelor nestructurale
(fara luarea in considerare a deformatiilor in timp);
sageata
de scurta durata din incarcarea de exploatare care
actioneaza inainte de executarea elementelor nestructurale
(fara luarea in considerare a deformatiilor in timp);
![]() sageata
de scurta durata din incarcarea totala de exploatare
(fara luarea in considerare a deformatiilor in timp);
sageata
de scurta durata din incarcarea totala de exploatare
(fara luarea in considerare a deformatiilor in timp);
![]() sageata
de scurta durata (fara luarea in considerare a
deformatiilor in timp) din incarcarea utila produsa de
aglomeratie de oameni;
sageata
de scurta durata (fara luarea in considerare a
deformatiilor in timp) din incarcarea utila produsa de
aglomeratie de oameni;
![]() -
sageata totala din incarcarile considerate in calculul la
oboseala;
-
sageata totala din incarcarile considerate in calculul la
oboseala;
qE - incarcarea totala de exploatare;
![]() - fractiune a incarcarii totale
de exploatare qE care se aplica inainte de executarea
elementelor nestructurale;
- fractiune a incarcarii totale
de exploatare qE care se aplica inainte de executarea
elementelor nestructurale;
q0 - incarcarile considerate in calculul la oboseala.
1 MODULII DE RIGIDITATE
Marimea sagetilor fiind dependenta de modulii de rigiditate ai elementelor de beton armat, se impune determinarea acestor rigiditati, corespunzator comportarii reale, in stadiul de exploatare.
Se defineste ca modul de rigiditate, produsul dintre modulul de deformatie, corespunzator materialului din care este alcatuit elementul, si caracteristica geometrica a sectiunii.
In cazul general al elementelor solicitate la incovoiere cu forta axiala, modulul de rigiditate se determina pornind de la legea de variatie a curburii elementului:
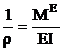 (1)
(1)
de unde rezulta:
 (2)
(2)
in care f = 1/r este curbura fibrei medii deformate (rotirea specifica), ME fiind momentul incovoietor din incarcarile de exploatare.
Pe baza deformatei fibrei medii, se poate scrie (fig. 1):
![]() (3)
(3)
Avand
in vedere ca ![]() , relatia (3) se scrie sub forma:
, relatia (3) se scrie sub forma:
 (4)
(4)
Inlocuind curbura medie data de relatia (4), in relatia (2), se obtine urmatoarea expresie de calcul a modulului de rigiditate:
 (5)
(5)
in care
inaltimea zonei comprimate x, modulul
de deformatie al betonului ![]() si efortul unitar
de compresiune in beton
si efortul unitar
de compresiune in beton ![]() se determina, in
stadiul II de serviciu, conform punctului 4.2.2.3.
se determina, in
stadiul II de serviciu, conform punctului 4.2.2.3.
In cazul elementelor din beton armat solicitate la incovoiere, STAS 10107/0-90 permite utilizarea relatiei:
![]() (6)
(6)
in care Ibi este momentul de inertie al sectiunii ideale de beton, calculat cu relatia (4.8).

In cazul elementelor solicitate preponderent la compresiune, in calculul deformatiilor axiale modulul de rigiditate axial EA are valoarea:
![]() (6)
(6)
In cazul elementelor solicitate preponderent la intindere, modulul de rigiditate axial EA are valoarea:
![]() (7)
(7)
in care indicele de conlucrare cu armatura longitudinala y se determina cu relatia (11.8) sau cu ajutorul anexei 22.
2 CALCULUL SAGETILOR ELEMENTELOR INCOVOIATE
Se admite ca sagetile sa fie determinate dupa regulile structurilor omogene, elastice, introducand pentru modulul de rigiditate EI valorile calculate la punctul 13.1.
In cazul grinzilor static determinate, sageata maxima se determina cu relatia:
![]() (8)
(8)
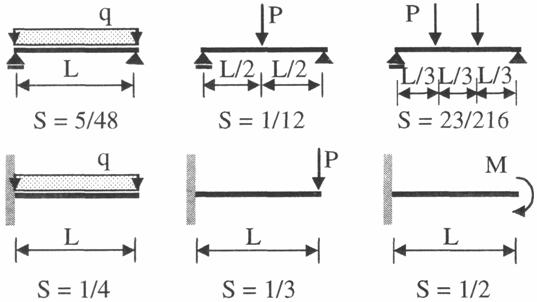
unde S este un coeficient ce depinde de tipul incarcarii si modul de rezemare (fig. 2).
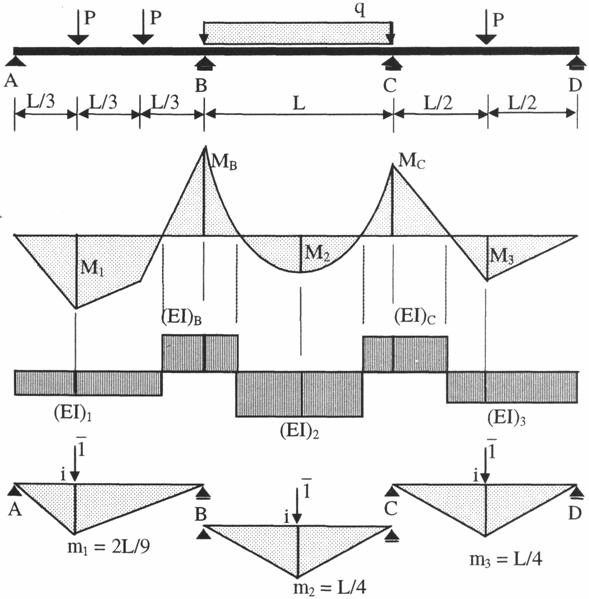
Pentru grinzile continue, determinarea sagetilor produse de un sistem de sarcini, in cazul problemei plane, se poate face operativ cu metoda Maxwel-Mohr (fig. 3). Astfel, pentru determinarea sagetii intre doua reazeme consecutive, intr-un punct i, se utilizeaza diagrama reala de momente dintre cele doua reazeme si diagrama de momente virtuala, rezultata din actiunea sarcinii unitare in punctul i, pe structura static determinata.
Pentru fiecare portiune de moment incovoietor de acelasi semn, valoarea modulului de rigiditate se considera constanta si egala cu valoarea modulului de rigiditate minim, care corespunde sectiunii cu cel mai mare moment incovoietor. In cazurile in care valorile EI calculate pentru zonele de moment pozitiv si negativ nu difera intre ele cu mai mult de 50%, se admite sa se considere pentru EI o valoare unica, egala cu semisuma valorilor respective.
Pentru sistemele de bare drepte cu solicitarea dominanta de incovoiere, daca l > 8h, se poate neglija influenta fortelor taietoare si axiale; sageata se poate determina in acest caz cu relatia Maxwel-Mohr:
![]() (9)
(9)
unde:
M este diagrama momentelor incovoietoare din sarcinile reale pe sistemul static nedeterminat;
mi - diagrama de momente virtuala, din sarcina virtuala aplicata in punctul i, dupa directia deplasarii, pe sistemul de baza (static determinat sau cu grad de nedeterminare mai redus);
l - lungimea barei pentru care se determina sageata;
EI - este modulul de rigiditate, considerat constant pe intervalul dat.
Efectuarea integralei (9) se poate face si dupa regula Veresceaghin, adica:
![]() (10)
(10)
unde:
W este suprafata diagramei reale de momente de pe bara pentru care se calculeaza sageata intre doua reazeme consecutive;
Jg - ordonata diagramei de momente virtuale mi, masurata in dreptul centrului de greutate al suprafetei W
Aplicatia numerica 12 Verificarea la starea limita de deformatie a unui element din beton armat supus la incovoiere.
Se cere verificarea sagetii unei grinzi incovoiate cu sectiunea dreptunghiulara (fig. Apl.12). Grinda este simplu rezemata si face parte dintr-un planseu prefabricat, urmand sa sustina elemente nestructurale care se pot deteriora in cazul unor deformatii prea mari. Se cunosc: b/h/h0 = 250/550/510 mm; calitatile materialelor: Bc25 (Eb = 30000 N/mm2) si PC52 (Ea = 210000 N/mm2); din calculul la incovoiere in sectiuni normale, la starea limita de rezistenta, a rezultat armatura longitudinala Aa = 1570 mm2 (5f20).
Incarcarile de exploatare actioneaza uniform distribuit, avand urmatoarele valori de calcul, egale cu intensitatile normate:
greutatea proprie a elementelor structurale = 14,70 kN/m
greutatea finisajelor (tencuiala si pardoseala) = 4,14 kN/m
greutatea peretilor despartitori = 3,00 kN/m
incarcarea utila = 15,00 kN/m

- incarcarea totala de exploatare:
qE = 14,7 + 4,14 + 3,0 + 15,0 = 37,0 kN/m;
- fractiunea de lunga durata a incarcarii de exploatare:
![]()
- partea din incarcarea de exploatare care se aplica inainte de executarea elementelor nestructurale:
![]()
Calculul sagetii fld (qE)
Aceasta sageata se determina din actiunea incarcarii totale de exploatare, deoarece se considera ca aceasta poate actiona cu toata valoarea ei timp indelungat.
Valoarea corectata a modulului de elasticitate al betonului se determina cu relatia (4.3):

Deoarece toate incarcarile actioneaza in acelasi mod (uniform distribuit), influenta actiunii de lunga durata rezulta:

Din
relatia (5.44) se determina ![]() , unde j0
rezulta din anexa 5, iar k1 = k2 = k3 = 1,0 (anexa 7), in cazul unor unor
conditii normale de solicitare a elementului si de umiditate a mediului.
, unde j0
rezulta din anexa 5, iar k1 = k2 = k3 = 1,0 (anexa 7), in cazul unor unor
conditii normale de solicitare a elementului si de umiditate a mediului.
Coeficientul de echivalenta se determina cu relatia:
![]()
Momentul de inertie al sectiunii ideale de beton necesita determinarea pozitiei axei neutre, utilizand relatiile (4.4b si 4.8):
![]()
![]() rezulta x = 249
mm
rezulta x = 249
mm
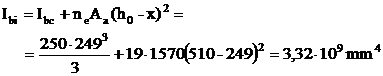
Modulul de rigiditate se determina din relatia (6):
![]()
Sageata
se calculeaza conform figurii 2, (grinda simplu rezemata, cu
incarcari uniform distribuite) cu relatia (8), in care ![]()
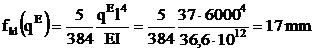
Calculul sagetii fsd ![]()
Aceasta sageata se determina din incarcarea de exploatare aplicata pana la executarea elementelor structurale care se pot deteriora, respectiv a incarcarii utile; se admite ca sageata produsa de aceste incarcari nu este afectata de fenomenele de durata, deoarece restul de incarcari pot sa actioneze intr-un timp scurt de la executie. Se procedeaza ca mai sus.
![]()
![]()
![]() ; rezulta
; rezulta
![]() rezulta x = 188
mm
rezulta x = 188
mm
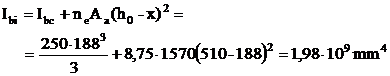
![]()

Verificarea la starea limita de deformatie se refera la suplimentul de sageata care se produce dupa executarea elementelor nestructurale si influenteaza deformarea acestora:
![]()
Valoarea admisa a suplimentului de sageata este, conform tabelului 1:
![]()
Deoarece Df = 11,8 mm < Dfadm =15 mm, conditia de verificare este satisfacuta.
[1] Prin prescriptii speciale, bine justificate, se pot admite si alte valori maxime ale sagetilor, precum si limitari de sageti pentru alte tipuri de elemente, necuprinse in tabelul 1.
|
Politica de confidentialitate |
| Copyright ©
2025 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |