
Teoria clasica a controlului automat este considerata astazi restrictiva, pentru ca este aplicabila numai sistemelor liniare cu parametri invarianti in timp, avand o singura intrare si o singura iesire (SISO). Functiile de intrare sunt restranse la cateva clase: treapta, impuls, sinusoida. Teoria clasica utilizeaza tehnici de proiectare in domeniul complex, bazate pe proceduri de minimizare care - in general - nu duc la solutii optimale.

Figura III.1. Structura teoriei moderne a controlului automat
Teoria moderna a controlului automat este mult mai complexa, permitand abordarea sistemelor cu parametri varianti sau nu in timp, liniare sau neliniare, multivariabile la intrare si iesire (MIMO). Proiectarea acestora este efectuata esential in domeniul timp, pe baza conceptului de stare interna a sistemului si vizeaza obtinerea unor solutii de control optimale pe baza unor proceduri sistematice si a unor indici de performanta prescrisi. Controlul optimal se refera atat la sisteme deterministe, cat si la cele stochastice.
Cmponentele teoriei moderne a controlului pot fi definite ca in Figura III.1, intr-un spatiu cu patru dimensiuni (obiectivul controlului w, procedura de proiectare x, sistemul fizic y si functia z). In acest spatiu pot fi evidentiate sase abordari de baza ale controlului automat contemporan: cu reactie, optimal/robust, adaptiv pasiv, adaptiv activ, instruibil si inteligent, cu parametri distribuiti.
Controlul optimal urmareste elaborarea unor decizii de comanda care sa minimizeze, in conditiile existentei anumitor restrictii, deviatia sistemului de la comportamentul ideal. In cazul discret, sistemul este descris prin:
![]() (1.1)
(1.1)
Cerintele de calitate impuse acestuia sunt evaluate printr-un indice global de performanta de forma:
![]() (1.2)
(1.2)
Problema consta in a gasi o comanda optimala u(n) care sa duca sistemul (1.1) din conditiile initiale de stare, date prin x= x(0), in conditiile finale de stare x= x(N), corespunzatoare obiectivului vizat. Traiectoria de stare de la x(0) la x(N) se obtine prin minimizarea indicelui (1.2), in conditiile restrictive:
![]() (1.3)
(1.3)

Figura III.2. Schema de principiu a controlului robust
Strategiile de control robust pentru sisteme liniare se bazeaza pe o prelucrare a erorii de catre un model intern (compensator), dupa o schema similara cu cea din Figura III.2, combinand controlul direct cu cel cu reactie. Tehnicile robuste iau in considerare variatiile parametrilor sistemului, adica modificarile punctului sau de functionare. Deoarece se presupune ca modelul matematic al sistemului condus nu este cunoscut, modelul intern este construit cu date experimentale obtinute off-line. Controlerul va utiliza initial aceste date, fiind insa supus unui proces ulterior de acordare on-line.
Un controler robust este proiectat astfel incat atat functia de transfer dintre perturbatia externa si iesire cat si cea dintre intrarea referinta si iesire sa aiba expresii dinainte stabilite. Cum aceste functii pot fi proiectate separat, controlerul se mai numeste compensator cu doua grade de libertate.
O alta tehnica de control robust, permite obtinerea unui observer al perturbatiei echivalente. Daca scriem ecuatia unui motor:
![]() (1.4)
(1.4)
unde Ja, T1, Kt, ![]() si ia
reprezinta respectiv inertia, cuplul extern, constanta de cuplu,
viteza si curentul rotoric, aplicand transformata Laplace membrilor stang
si drept ai ecuatiei obtinem:
si ia
reprezinta respectiv inertia, cuplul extern, constanta de cuplu,
viteza si curentul rotoric, aplicand transformata Laplace membrilor stang
si drept ai ecuatiei obtinem:
![]() (1.5)
(1.5)
Am notat cu Te(s) o perturbatie ehivalenta de forma:
![]() (1.6)
(1.6)
Ecuatia (1.5) se poate rescrie:
![]() (1.7)
(1.7)
Semnul " " reprezinta valoarea nominala, iar "D" abaterea de la aceasta valoare, obtinuta printr-un filtru trece jos de tipul 1/(s+kf). Valoarea estimata a lui Te(s) este:
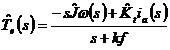 (1.8)
(1.8)
Cu scopul de a anula perturbatia
echivalenta, care include si variatiile parametrilor sistemului,
la intrarea acestuia se aplica ![]() . In continuare, se proiecteaza un controler cu
reactie, utilizand valorile nominale ale parametrilor.
. In continuare, se proiecteaza un controler cu
reactie, utilizand valorile nominale ale parametrilor.
Controlul adaptiv este extrem de atragator, pentru ca permite realizarea unor sisteme de reglare automata capabile sa se acomodeze la schimbari neprevazute ale mediului de operare sau sa poata functiona si in conditiile unor avarii minore. In Figura III.3 sunt prezentate trei scheme de control adaptiv: cu modificarea amplificarii (a), cu model de referinta (b) si cu autoacordare (c).
Adaptarea cu modificarea amplificarii este o schema in bucla deschisa comparabila cu compensatorul direct. Compensarea fara reactie are avantajul ca permite modificarea rapida a parametrilor controlerului si reprezinta o tehnica predominant utilizata pentru proiectarea sistemelor industriale de control automat de inalta performanta.
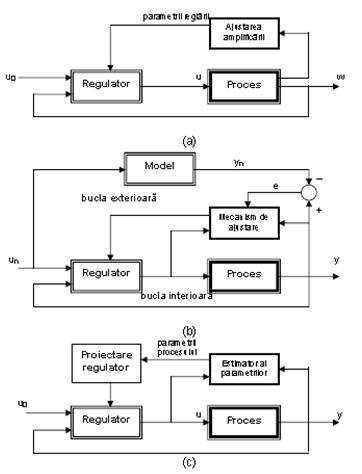
Figura III.3. Diferite arhitecturi pentru controlul adaptiv
Adaptarea cu model de referinta (MRAC)
utilizeaza acest model pentru a indica cum ar trebui sa
raspunda ideal iesirea procesului la semnalul de comanda.
Modelul este o parte a sistemului de control. Reglarea se face in doua
bucle. Cea interioara este una banala, compusa din proces
si regulator. Parametrii regulatorului sunt ajustati prin bucla
exterioara astfel incat eroarea e=
![]() -y intre
iesirea modelului si cea a sistemului sa fie cat mai mica.
Mecanismul de ajustare se bazeaza pe modificarea amplificarii.
Tehnicile MRAC sunt mai putin adecvate pentru actionarile
electrice, pentru ca sunt sensibile la perturbatii, ridica
probleme de stabilitate si au un
raspuns tranzitoriu lung.
-y intre
iesirea modelului si cea a sistemului sa fie cat mai mica.
Mecanismul de ajustare se bazeaza pe modificarea amplificarii.
Tehnicile MRAC sunt mai putin adecvate pentru actionarile
electrice, pentru ca sunt sensibile la perturbatii, ridica
probleme de stabilitate si au un
raspuns tranzitoriu lung.
Adaptarea prin autoacordarea parametrilor se face tot prin doua bucle. Cea exterioara este compusa dintr-un estimator parametric recursiv si un model de calcul. Modelul este o solutie rezultata din proiectarea on-line a unui sistem cu parametri cunoscuti. Autoadaptarea se bazeaza pe tehnici clasice, cum ar fi marginea de faza sau de amplitudine, alocarea polilor, metoda minimei variante sau metoda liniar-patratica gaussiana. Pentru estimarea parametrilor pot fi utilizate mai multe scheme: aproximarea stochastica, minimul patratic, metoda variabilelor instrumentale, filtrarea Kalman extinsa, etc.
Intre teoria si practica controlului automat adaptiv exista insa un mare decalaj. Pentru a obtine o apropiere a celor doua domenii, care sa permita elaborarea unor solutii cu adevarat practice pentru aplicatiile industriale, sunt necesare inca multe cercetari.
|
Politica de confidentialitate |
| Copyright ©
2025 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |