
Dezvoltarea multipolara a potentialului vector
Fie
distributia de curenti din volumul V' caracterizata in fiecare
punct ![]() prin densitatea de curent
prin densitatea de curent
![]() (fig. 5).
(fig. 5).
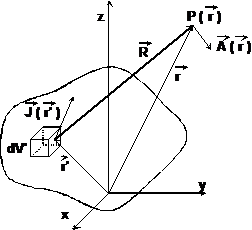
Figura 5.
Potentialul
vector al unei astfel de distributii de curenti, in punctul P(![]() ) este:
) este:
![]() (36)
(36)
unde ![]() . Alegand
. Alegand ![]() pentru orice element de volum dV' al distributiei,
expresia (36) poate fi dezvoltata in serie dupa puterile lui r'/r. In
acest fel potentialul vector capata forma:
pentru orice element de volum dV' al distributiei,
expresia (36) poate fi dezvoltata in serie dupa puterile lui r'/r. In
acest fel potentialul vector capata forma:
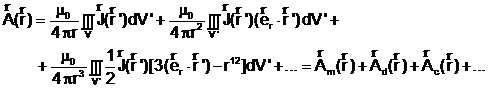 (37)
(37)
unde ![]() . sunt respectiv
contributiile de monopol, de dipol de cuadrupol, etc., in potentialul
vector total in punctul P(
. sunt respectiv
contributiile de monopol, de dipol de cuadrupol, etc., in potentialul
vector total in punctul P(![]() ).
).
Ca
si pentru potentialul electric, dependenta acestor termeni de
distanta r este de forma 1/r, 1/r2, etc. De asemenea, in
fiecare termen din dezvoltare, integrandul depinde atat de coordonatele
distributiei de curenti (prin ![]() ), cat si de coordonatele punctului de observatie
(prin
), cat si de coordonatele punctului de observatie
(prin ![]() ). Este utila separarea celor doua tipuri de
variabile.
). Este utila separarea celor doua tipuri de
variabile.
Se
poate arata ca termenul de monopol magnetic din relatia (37)
este nul. Intr-adevar, curentii electrici stationari sunt
curenti pe circuite inchise si sediul acestor curenti este
volumul V'. Deci curentii din V' pot fi imaginati ca circuland prin
tuburi de curent inchise care umplu volumul, fara sa iese din
el. Daca curentul prin al j-lea tub de curent a carei sectiune
transversala este aj, o notam prin Ij, atunci
integrala din ![]() poate fi
exprimata astfel:
poate fi
exprimata astfel:
![]()
unde insumarea se face asupra tuturor tuburilor de
curent din V', iar integrala din ![]() se calculeaza pe
circuitul inchis Cj al tubului de curent. Evident
se calculeaza pe
circuitul inchis Cj al tubului de curent. Evident ![]() . Trecerea vectorului de la densitatea de curent
. Trecerea vectorului de la densitatea de curent ![]() la elementul de drum
la elementul de drum ![]() este posibila,
deoarece cei doi vectori au aceeasi orientare. Deoarece fiecare tub de
curent este un circuit inchis
este posibila,
deoarece cei doi vectori au aceeasi orientare. Deoarece fiecare tub de
curent este un circuit inchis ![]() , ceea ce demonstreaza ca termenul de monopol
da contributie nula in potentialul campului magnetic,
adica
, ceea ce demonstreaza ca termenul de monopol
da contributie nula in potentialul campului magnetic,
adica ![]()
Pentru
a putea obtine o interpretare fizica expresiei potentialului
vector, integrala ![]() va fi
inmultita cu un vector constant si arbitrar
va fi
inmultita cu un vector constant si arbitrar ![]() :
:
![]()
Impartind
integrandul acestei expresii in doua jumatati si
adunand si scazand din fiecare jumatate termenul ![]() , se poate scrie:
, se poate scrie:
![]()
unde
![]() (38)
(38)
si
![]() (39)
(39)
Se
poate arata ca ![]() . In aceste conditii, se poate scrie:
. In aceste conditii, se poate scrie:
![]() (40)
(40)
de unde
![]() (41)
(41)
Vectorul ![]() poate fi scos de sub
integrala deoarece acesta nu depinde de variabilele de integrat. Se
constata ca termenul din paranteza patrata depinde numai de
coordonatele distributiei curentilor.
poate fi scos de sub
integrala deoarece acesta nu depinde de variabilele de integrat. Se
constata ca termenul din paranteza patrata depinde numai de
coordonatele distributiei curentilor.
Introducand momentul de dipol magnetic al distributiei de curenti din V' prin relatia:
![]() (42)
(42)
si inlocuind (42) in termenul dipolar din (37) se obtine:
![]() (43)
(43)
Din
(43) se constata ca potentialul vector al dipolului magnetic
este un vector orientat normal la planul format de vectorii ![]() si
si ![]() .
.
Pentru deducerea relatiei (37) nu s-a impus nici o restrictie legata de distributia de curenti, deci rezultatele obtinute sunt generale. O distributie particulara des utilizata practic este o bucla plana de curent de forma arbitrara. Pentru o astfel de bucla se poate scrie:
![]()
si (42) devine:
![]() (44)
(44)
Integrala pe conturul buclei este egala cu aria S a buclei. Prin urmare:
![]() (45)
(45)
unde ![]() este versorul normalei
la suprafata orientata S. Sensul sau este dat de sensul de
inaintare al unui burghiu drept ce este rotit in sensul curentului care
circula prin bucla. Din (43) se obtine:
este versorul normalei
la suprafata orientata S. Sensul sau este dat de sensul de
inaintare al unui burghiu drept ce este rotit in sensul curentului care
circula prin bucla. Din (43) se obtine:
![]() (46)
(46)
Pornind de la relatia (43) si tinand seama de legatura dintre potentialul magnetic vector si inductia magnetica, se obtine:
![]() (47)
(47)
|
Politica de confidentialitate |
| Copyright ©
2025 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |