
Estimatoare de viteza, pozitie si flux pentru aplicatii cu performante ridicate
1. Introducere
In cele ce urmeaza estimatoarele de viteza se obtin prin considerarea ecuatiilor de tensiune ale masinii asincrone. Schemele descrise in continuare monitorizeaza tensiunile statorice si curentii sau monitorizeaza curentii si reconstruiesc tensiunile statorice.
Unele dintre aceste scheme de estimare se folosesc in actionarile electrice industriale, fara senzori de viteza, disponibile pe piata. Totusi, este important de observat ca, in general, precizia estimatoarelor in bucla deschisa depinde in mare masura de precizia folosita pentru determinarea parametrilor masinii. La viteze reduse ale rotorului, precizia estimatoarelor in bucla deschisa este redusa si deviatia parametrilor de la valorile lor reale are o mare influenta asupra performantei in regim stationar si in regim tranzitoriu a actionarilor care folosesc estimatoare in bucla deschisa. O precizie mai mare este atinsa daca fluxul statoric se obtine cu o schema care evita integratoarele pure [21].
In general, estimatoarele in bucla deschisa depind de diferiti parametri ai masinii asincrone. Rezistenta statorica (Rs) are un efect important asupra fluxului statoric, in special la viteze reduse si daca fluxul rotoric se obtine din cel statoric, atunci precizia fluxului rotoric este influentata de rezistenta statorica. Este posibil sa avem mai degraba o estimare precisa a rezistentei statorice 'fierbinti' (la temperatura ridicata) prin folosirea modelului termic al masinii asincrone.
In unele scheme, fluxul rotoric estimat necesita cunoasterea constantei de timp rotorice, care poate de asemenea varia, deoarece ea este raportul dintre inductivitatea proprie a rotorului si rezistenta rotorului; rezistenta rotorului poate varia datorita temperaturii si efectului pelicular iar inductivitatea proprie poate varia datorita efectului pelicular si datorita efectelor saturatiei.
Schimbarile
rezistentei rotorice datorita schimbarilor de temperatura
sunt, in mod obisnuit, schimbari lente. Datorita saturatiei
fluxului principal, inductivitatea de magnetizare (Lm) se poate schimba si astfel inductivitatea
proprie a rotorului ![]() se poate de asemenea
schimba chiar daca inductivitatile de scapari (Ls, Lr) sunt constante.
se poate de asemenea
schimba chiar daca inductivitatile de scapari (Ls, Lr) sunt constante.
Schimbarile
inductivitatii proprii a rotorului datorita saturatiei pot
fi rapide. Datorita saturatiei fluxului de scapari, Ls, Lr si
inductivitatea tranzitorie a statorului ![]() se pot de asemenea
schimba.
se pot de asemenea
schimba.
Intr-o actionare cu reglarea cuplului, efectele parametrilor incorecti au drept rezultat cuplu incorect, flux incorect, degradarea performantei sistemului, etc.
2. Scheme imbunatatite pentru estimatoare de viteza, pozitie si flux
Schema 1
Este posibil sa obtinem direct o expresie pentru viteza rotorului folosind ecuatia fazoriala a tensiunii rotorice (rel. 2.18) exprimata in sistemul de referinta fix d - q ( = 0). Din (2.18) ecuatia tensiunii rotorice dupa axa reala devine (a se vedea rel. 2.20), renuntand la indicele
![]() , (6.13)
, (6.13)
unde, (conform 2.75)
![]() . (6.14)
. (6.14)
Ecuatia (6.13) contine curentul rotoric in axa d care nu poate fi masurat direct. Totusi, inlocuind (6.14) in (6.13) rezulta viteza unghiulara r in functie de componenta dupa axa d a curentului statoric. Se obtine:
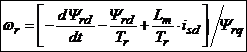 . (6.15)
. (6.15)
Aceasta ecuatie se poate utiliza pentru estimarea vitezei rotorului. Pentru aceasta trebuie estimate componentele fluxului rotoric dupa axa d si axa q.
Pentru aceasta se scriu ecuatiile (2.74 si 2.75) in sistemul d - q astfel:
![]() , (6.16)
, (6.16)
![]() . (6.17)
. (6.17)
Inlocuind ![]() (din rel. 6.16) in
rel. 6.17, tinand seama ca
(din rel. 6.16) in
rel. 6.17, tinand seama ca ![]() si ca
inductivitatea tranzitorie a statorului
si ca
inductivitatea tranzitorie a statorului ![]() , rezulta:
, rezulta:
![]() . (6.18)
. (6.18)
Din ecuatia (6.18) se obtine:
![]() , (6.19)
, (6.19)
![]() . (6.20)
. (6.20)
Derivata lui
![]() se utilizeaza in
rel. (6.15). Neglijand saturatia, din (6.19) rezulta ca:
se utilizeaza in
rel. (6.15). Neglijand saturatia, din (6.19) rezulta ca:
![]() , (6.21)
, (6.21)
Ecuatiile (6.19 si 6.21) contin componentele fluxului statoric, care se pot obtine din ecuatia (2.3):
![]() , (6.22)
, (6.22)
![]() . (6.23)
. (6.23)
Ecuatia (6.21), tinand seama de (6.22), devine:
![]() , (6.24)
, (6.24)
si ![]() rezulta printr-o
integrare. In mod similar,
rezulta printr-o
integrare. In mod similar, ![]() se obtine din:
se obtine din:
 , (6.25)
, (6.25)
prin integrare. O implementare posibila este indicata in fig. 6.4. conform relatiilor (6.24), (6.25) si (6.15).
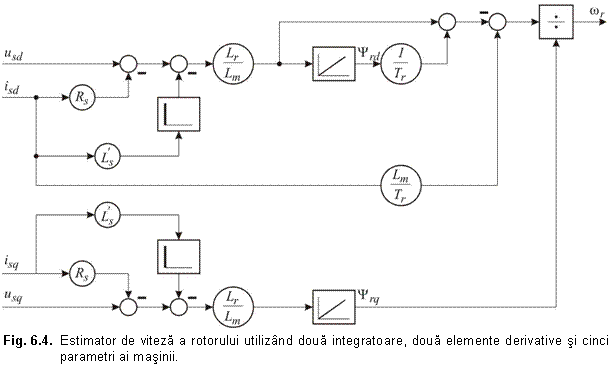
Se
poate observa ca aceasta schema necesita diferiti
parametri ai masinii care variaza cu temperatura, efectul pelicular
si saturatia. Deci se poate obtine o viteza precisa
daca acesti parametri sunt precis cunoscuti. La viteze reduse
precizia acestei scheme este limitata, dar se pot obtine
imbunatatiri folosind alte tehnici de estimare a fluxului. O
schema imbunatatita se obtine utilizand
urmatoarea tehnica [21].
Din ecuatia fazoriala a tensiunii statorice, scrisa in sistem bifazat fix d - q (rel. 2.3), rezulta componentele bifazate ale derivatei fluxului statoric (ecuatiile 2.5):
![]() , (6.26)
, (6.26)
![]() . (6.27)
. (6.27)
Se
orienteaza sistemul bifazat dupa fluxul statoric (fig. 4.14). In
acest caz ![]() (ecuatia 2.13).
Ecuatia fazoriala a tensiunii statorice in sistemul ds - qs, orientat
dupa fluxul statoric (ec. 2.15) devine:
(ecuatia 2.13).
Ecuatia fazoriala a tensiunii statorice in sistemul ds - qs, orientat
dupa fluxul statoric (ec. 2.15) devine:
![]() , (6.28)
, (6.28)
deoarece ![]() . Din ecuatia (6.28) componentele dupa axele ds si qs vor fi:
. Din ecuatia (6.28) componentele dupa axele ds si qs vor fi:
![]() , (6.29)
, (6.29)
![]() . (6.30)
. (6.30)
Din ecuatiile (6.29) si (6.30) rezulta:
![]() , (6.31)
, (6.31)
si
![]() . (6.32)
. (6.32)
Acestea
constituie iesirile din blocul ![]() (fig. 6.5). Prin
integrarea ecuatiei (6.31) rezulta fluxul statoric
(fig. 6.5). Prin
integrarea ecuatiei (6.31) rezulta fluxul statoric ![]() iar prin
impartirea relatiei (6.32) cu
iar prin
impartirea relatiei (6.32) cu ![]() si apoi prin
integrare rezulta pozitia fluxului statoric (unghiul s). Aceste blocuri, care constituie
estimatorul de flux, sunt marcate in schema din figura 6.5 prin blocul figurat
cu linie punctata. In continuare, prin blocul de transformare
polar-cartezian (P → C) se determina componentele fluxului statoric
si apoi prin
integrare rezulta pozitia fluxului statoric (unghiul s). Aceste blocuri, care constituie
estimatorul de flux, sunt marcate in schema din figura 6.5 prin blocul figurat
cu linie punctata. In continuare, prin blocul de transformare
polar-cartezian (P → C) se determina componentele fluxului statoric ![]() dupa axele d - q atasate statorului.
dupa axele d - q atasate statorului.
![]() si
si ![]() (6.33)
(6.33)
In
continuare utilizand relatiile (6.19) si (6.20) se determina
fluxurile rotorice ![]() si
si ![]() , iar cu relatia (6.15) rezulta viteza
unghiulara a rotorului
, iar cu relatia (6.15) rezulta viteza
unghiulara a rotorului ![]() .
.
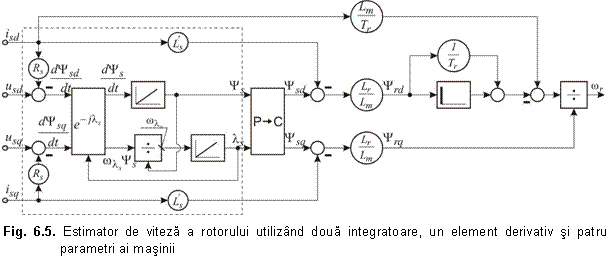
Estimatorul prezentat in figura 6.5
contine un element derivativ pentru a obtine ![]() . Daca se foloseste un algoritm numeric potrivit,
derivarea se poate executa precis.
. Daca se foloseste un algoritm numeric potrivit,
derivarea se poate executa precis.
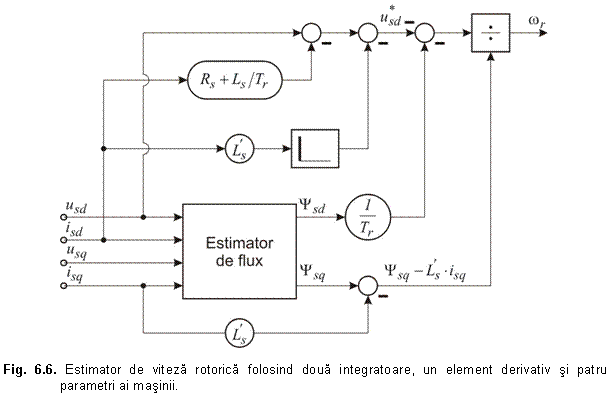
Schema 2
Este posibil sa obtinem o alta schema de estimare a vitezei rotorului daca ecuatiile (6.19), (6.20) si (6.24) se inlocuiesc in ecuatia (6.15). Astfel rezulta:
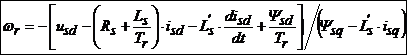 . (6.34)
. (6.34)
Ar putea fi
aratat ca aceeasi expresie se poate obtine direct daca
se considera ecuatia tensiunii rotorice in axa d, ecuatia (6.13) si se inlocuiesc in aceasta
ecuatiile (6.20), (6.24) si ![]() (care rezulta din definitia fluxului statoric in
axa d,
(care rezulta din definitia fluxului statoric in
axa d, ![]() ). Schema estimatorului folosind ecuatia (6.34) este
reprezentata in figura 6.6. Blocul estimator de flux poate fi implementat
folosind oricare din tehnicile imbunatatite discutate mai
devreme.
). Schema estimatorului folosind ecuatia (6.34) este
reprezentata in figura 6.6. Blocul estimator de flux poate fi implementat
folosind oricare din tehnicile imbunatatite discutate mai
devreme.
Estimatorul de viteza din figura (6.6) necesita patru parametri ai masinii si precizia estimatorului depinde mult de acestia. Totusi, este posibil sa se obtina rezultate satisfacatoare pana la 1 - 2 Hz.
Ecuatia (6.34) a rezultat folosind ecuatia de tensiune a rotorului in axa d, dar daca se utilizeaza ecuatia de tensiune a rotorului in axa q, se poate obtine in mod asemanator:
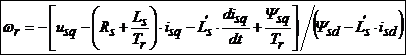 . (6.35)
. (6.35)
O
implementare bazata pe ecuatia (6.35) necesita aceeasi
complexitate ca aceea prezentata in figura (6.6). Totusi, dupa
cum se poate vedea din ecuatia (6.35) rezulta ca daca se
utilizeaza un alt estimator, in care fluxul dupa axa q se forteaza sa fie
zero, schema se simplifica si numaratorul nu va mai contine
![]() . Acest caz se va discuta in continuare.
. Acest caz se va discuta in continuare.
Schema 3
Exista multe posibilitati pentru a obtine viteza rotorului, dar este foarte simplu sa folosim mai intai ecuatia de tensiune a rotorului in sistemul de referinta fix, d - q si apoi, ecuatia rezultanta sa se transforme in sistemul orientat dupa fluxul statoric [21]. Urmand aceasta conceptie vor rezulta desigur ecuatiile (6.34) si (6.35). In acest scop se considera fazorul spatial al tensiunii rotorice in sistemul de referinta statoric d - q. Acesta se obtine din ecuatia (2.18) presupunand = 0 si astfel:
![]() ,
,
sau
renuntand la indicele
si notand ![]() ;
; ![]() vom avea:
vom avea:
![]() .
.
Fazorul spatial al curentului rotoric se poate elimina considerand ecuatia (5.3):
![]()
si ecuatia (5.4),
![]() .
.
Deoarece:
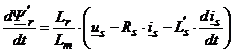 ,
,
inlocuind
expresiile pentru ![]() ,
, ![]() si
si ![]() in ecuatia
tensiunii rotorice rezulta:
in ecuatia
tensiunii rotorice rezulta:
 . (6.36)
. (6.36)
Se
observa ca, asa cum era de asteptat, partile
reale si imaginare ale ecuatiei (6.36) sunt ecuatiile (6.34)
respectiv (6.35). Ecuatia (6.36) este o forma specifica a ecuatiei
tensiunii rotorice intr-un sistem de referinta fix, d - q. Cand aceasta ecuatie se
raporteaza la un sistem de referinta rotativ, orientat dupa
fazorul spatial al fluxului statoric, a carei viteza este ![]() (fig. 4.14) atunci,
conform relatiei (1.36), rezulta:
(fig. 4.14) atunci,
conform relatiei (1.36), rezulta:
 . (6.37)
. (6.37)
Din partea dreapta a ecuatiei (6.37):
![]() ,
,
si
![]() .
.
reprezinta fazorii spatiali ai fluxului statoric si respectiv curentului statoric in sistemul de referinta orientat dupa fluxul statoric.
Astfel se poate scrie:
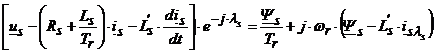 . (6.38)
. (6.38)
Partile reale si imaginare ale ecuatiei (6.38) conduc la:
![]() ; (6.39)
; (6.39)
![]() , (6.40)
, (6.40)

unde:
 (6.41)
(6.41)
si
![]() ,
, ![]() . Din ecuatia (6.40) rezulta ca:
. Din ecuatia (6.40) rezulta ca:
![]() . (6.42)
. (6.42)
Cum
era si de asteptat numaratorul ecuatiei (6.42)
contine numai ![]() si nu
contine componenta
si nu
contine componenta ![]() a fluxului statoric (a
se vedea ecuatia (6.35)). Fizic, aceasta se datoreste faptului
ca in sistemul de referinta orientat dupa fluxul statoric
componenta in cuadratura a fluxului statoric este zero. In figura (6.7)
este implementata ecuatia (6.42) tinand seama si de
ecuatia (6.41).
a fluxului statoric (a
se vedea ecuatia (6.35)). Fizic, aceasta se datoreste faptului
ca in sistemul de referinta orientat dupa fluxul statoric
componenta in cuadratura a fluxului statoric este zero. In figura (6.7)
este implementata ecuatia (6.42) tinand seama si de
ecuatia (6.41).
Aceasta schema contine din nou patru parametri ai masinii si poate da rezultate satisfacatoare chiar la viteze foarte reduse. Tensiunile statorice pot fi monitorizate sau pot fi reconstruite din tensiunea de c.c. din circuitul intermediar al convertorului si din starile de comutatie ale invertorului (a se vedea subcap. 5.4). Un estimator de viteza bazat pe ecuatia (6.42) se poate utiliza eficace, in schemele de reglare cu orientare dupa fluxul statoric, chiar la frecvente statorice relativ reduse.
Daca
viteza rotorului este determinata de ecuatia (6.40), atunci utilizand
ecuatia (6.39), este posibil sa se obtina o expresie pentru
Trebuie
sa aratam ca este posibil sa se construiasca un
estimator de flux statoric sau rotoric in care problemele de deriva,
asociate cu cele ale integratoarelor 'pure' in bucla
deschisa la frecventa redusa, sunt evitate printr-o
integrare intr-o banda limitata a componentelor de frecventa
ridicata si prin inlocuirea estimarii imprecise a fluxului la
frecventa sub ![]() cu valoarea sa
impusa intr-o tranzitie usoara. In acest scop se
utilizeaza un element inertial de ordinul intai, cum se arata in
figura (6.8).
cu valoarea sa
impusa intr-o tranzitie usoara. In acest scop se
utilizeaza un element inertial de ordinul intai, cum se arata in
figura (6.8).
Intrarile
estimatorului de flux din figura (6.8) sunt valorile monitorizate ale fazorului
spatial al tensiunii statorice ![]() si ale fazorului
spatial al curentului statoric
si ale fazorului
spatial al curentului statoric ![]() in sistemul de axe
stationar (d - q). O a treia
intrare este modulul valorii impuse a fazorului spatial al fluxului
statoric
in sistemul de axe
stationar (d - q). O a treia
intrare este modulul valorii impuse a fazorului spatial al fluxului
statoric ![]() , exprimat in acealsi sistem de axe. Fazorul
spatial al valorii impuse a fluxului statoric
, exprimat in acealsi sistem de axe. Fazorul
spatial al valorii impuse a fluxului statoric ![]() contine doua
componente
contine doua
componente ![]() si
si ![]() . Din ecuatia (2.3) fazorul spatial al tensiunilor
statorice induse este:
. Din ecuatia (2.3) fazorul spatial al tensiunilor
statorice induse este:
![]()
si,
intr-un estimator de flux statoric in bucla deschisa - utilizand un integrator 'pur' -
valoarea sa integrata ![]() va produce fazorul
spatial al fluxului statoric
va produce fazorul
spatial al fluxului statoric ![]() . Totusi, in figura (6.8)
. Totusi, in figura (6.8) ![]() este multiplicat cu T. Fazorul spatial al fluxului
statoric impus adunat cu
este multiplicat cu T. Fazorul spatial al fluxului
statoric impus adunat cu ![]() produce
produce ![]() . Aceasta constituie intrarea in elementul inertial de
ordinul intai, cu functia de transfer
. Aceasta constituie intrarea in elementul inertial de
ordinul intai, cu functia de transfer ![]() . La iesirea acestui element se obtine valoarea
estimata a fazorului spatial al fluxului statoric
. La iesirea acestui element se obtine valoarea
estimata a fazorului spatial al fluxului statoric ![]() . Se poate vedea ca daca
. Se poate vedea ca daca ![]() este egal cu
este egal cu ![]() atunci iesirea
atunci iesirea ![]() este exact
este exact ![]() . In figura (6.8) se foloseste un convertor
cartezian-polar (C→P) care produce modulul
. In figura (6.8) se foloseste un convertor
cartezian-polar (C→P) care produce modulul ![]() si unghiul
si unghiul ![]() al fazorului spatial al fluxului statoric in sistemul de
referinta fix (fig. 4.14). Este posibil sa se obtina o
estimare a fazorului spatial al fluxului rotoric, exprimat in sistemul de
referinta fix,
al fazorului spatial al fluxului statoric in sistemul de
referinta fix (fig. 4.14). Este posibil sa se obtina o
estimare a fazorului spatial al fluxului rotoric, exprimat in sistemul de
referinta fix, ![]() , considerand ca, din ecuatia (5.4):
, considerand ca, din ecuatia (5.4):
![]() ,
,
unde
![]() este inductivitatea
statorica tranzitorie si aceasta estimare este de asemenea
prezentata in figura (6.8). Astfel se obtine
este inductivitatea
statorica tranzitorie si aceasta estimare este de asemenea
prezentata in figura (6.8). Astfel se obtine ![]() si folosind un
alt convertor C→P se obtin
si folosind un
alt convertor C→P se obtin ![]() si
si ![]() . Aceasta schema de estimator se poate folosi in
sistemul de reglare cu orientare dupa fluxul statoric si dupa
fluxul rotoric cat si in actionarile cu controlul direct al
cuplului. In actionarile cu orientare dupa fluxul statoric,
fazorul spatial
. Aceasta schema de estimator se poate folosi in
sistemul de reglare cu orientare dupa fluxul statoric si dupa
fluxul rotoric cat si in actionarile cu controlul direct al
cuplului. In actionarile cu orientare dupa fluxul statoric,
fazorul spatial ![]() se poate obtine
din modulul fazorului spatial al fluxului statoric impus
se poate obtine
din modulul fazorului spatial al fluxului statoric impus ![]() , care este una din intrarile in schema de reglare cu
orientare dupa fluxul statoric considerand ca:
, care este una din intrarile in schema de reglare cu
orientare dupa fluxul statoric considerand ca:

![]() ,
,
unde
![]() este unghiul fazorului spatial al fluxului statoric cu
axa reala a sistemului de referinta stationar (fix).
este unghiul fazorului spatial al fluxului statoric cu
axa reala a sistemului de referinta stationar (fix).
Trebuie
observat ca pentru functionarea la frecventa redusa,
in schema din figura (6.8), elementul inertial are o functie de
transfer aproximativ unitara si astfel iesirea sa devine aproape
egala cu ![]() , deoarece
, deoarece ![]() este mic. Aceasta este in acord cu ceea ce s-a stabilit mai
inainte. Totusi, la frecvente statorice ridicate, functia de
transfer a elementului inertial este aproximativ egala cu cea a unui
integrator si urmeaza ca cele doua actiuni se
comuta in jurul frecventei statorice
este mic. Aceasta este in acord cu ceea ce s-a stabilit mai
inainte. Totusi, la frecvente statorice ridicate, functia de
transfer a elementului inertial este aproximativ egala cu cea a unui
integrator si urmeaza ca cele doua actiuni se
comuta in jurul frecventei statorice ![]() .
. ![]() , unde Tr
este
, unde Tr
este
Schema 4
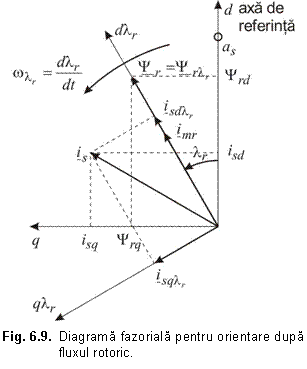
In cele ce urmeaza se va prezenta un estimator de viteza a rotorului care foloseste viteza unghiulara a fazorului spatial al fluxului rotoric. Acesta necesita estimarea frecventei de alunecare potrivite. Schema este una care se utilizeaza in actionarile fara senzori, de inalta performanta, introduse recent pe piata. In aceste implementari comerciale tensiunile statorice nu se monitorizeaza ci se reconstruiesc din tensiunea de c.c. din circuitul intermediar si din starile de comutatie ale invertorului (a se vedea subcap. 5.4). Este posibil sa implementam un estimator al pulsatiei de alunecare (2) cu considerarea ecuatiei tensiunii rotorice a motorului asincron (ec. 2.18):
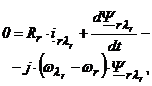 (6.43)
(6.43)
unde
![]() este fazorul
spatial al fluxului rotoric in sistemul de referinta d r - q r atasat fluxului rotoric (fig. 6. 9)
si definit de ecuatiile:
este fazorul
spatial al fluxului rotoric in sistemul de referinta d r - q r atasat fluxului rotoric (fig. 6. 9)
si definit de ecuatiile:
![]()
si,
![]() .
.
Din ecuatia (4.1) de definitie a curentului de magnetizare corespunzator fluxului rotoric rezulta:
![]() . (6.44)
. (6.44)
Inlocuirea ecuatiei (6.44) in ecuatia (6.43) conduce la urmatoarea ecuatie diferentiala a tensiunii rotorice, daca se neglijeaza saturatia magnetica (Lm = const.):
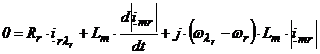 . (6.45)
. (6.45)
Din ecuatia (4.5) se poate scrie:
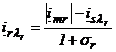 .
.
Prin inlocuirea acesteia in ecuatia (6.45) si prin impartirea cu Rr, se obtine o ecuatie care se poate pune sub forma ecuatiei unui element inertial de ordinul intai astfel:
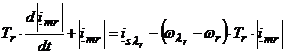 . (6.46)
. (6.46)
Rezolvand componentele dupa axa reala si imaginara se obtin ecuatii extrem de simple care descriu modelul de flux rotoric in sistemul de referinta orientat dupa
fluxul rotoric:
 , (6.47)
, (6.47)
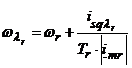 . (6.48)
. (6.48)
In
ecuatia (6.48) termenul ![]() reprezinta,
conform ecuatiei (6.8), pulsatia de alunecare a fluxului rotoric 2 si
urmeaza ca viteza unghiulara a fluxului rotoric
reprezinta,
conform ecuatiei (6.8), pulsatia de alunecare a fluxului rotoric 2 si
urmeaza ca viteza unghiulara a fluxului rotoric ![]() este egala cu suma dintre viteza unghiulara a
rotorului si pulsatia de alunecare a fluxului rotoric 2. Daca
este egala cu suma dintre viteza unghiulara a
rotorului si pulsatia de alunecare a fluxului rotoric 2. Daca ![]() este constant, din
ecuatia (6.47) rezulta ca
este constant, din
ecuatia (6.47) rezulta ca ![]() . Modulul fazorului spatial al fluxului rotoric
poate fi mentinut constant, la un nivel dorit, prin reglarea componentei
curentului statoric in axa directa
. Modulul fazorului spatial al fluxului rotoric
poate fi mentinut constant, la un nivel dorit, prin reglarea componentei
curentului statoric in axa directa ![]() , cum se vede din ecuatia (6.47), daca nu
exista slabire de camp (sub viteza de baza). Cuplul electromagnetic este determinat de
curentul statoric din axa in cuadratura
, cum se vede din ecuatia (6.47), daca nu
exista slabire de camp (sub viteza de baza). Cuplul electromagnetic este determinat de
curentul statoric din axa in cuadratura ![]() , conform cu ecuatia (4.8). Din ecuatia (6.48)
pulsatia de alunecare a fluxului rotoric este:
, conform cu ecuatia (4.8). Din ecuatia (6.48)
pulsatia de alunecare a fluxului rotoric este:
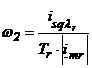 . (6.49)
. (6.49)
Trecerea de la sistemul bifazat d - q la sistemul (d - q ) se face conform ecuatiei (1.41):
![]()
sau
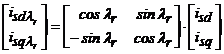 . (6.50)
. (6.50)
Inlocuind
expresia lui ![]() din ecuatia (6.50) in ecuatia (6.49) se
obtine:
din ecuatia (6.50) in ecuatia (6.49) se
obtine:
 . (6.51)
. (6.51)
unde r este unghiul fluxului rotoric fata de axa directa a sistemului de referinta stationar (fig. 6.9).
Considerand
ca modulul fluxului rotoric se poate exprima cu ![]() - conform ec. (4.1)
si folosind de asemenea relatiile:
- conform ec. (4.1)
si folosind de asemenea relatiile: ![]() ;
; ![]() (fig. 6.9),
ecuatia (6.51) poate fi scrisa ca:
(fig. 6.9),
ecuatia (6.51) poate fi scrisa ca:
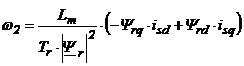 . (6.52)
. (6.52)
Ecuatia (6.52) poate fi utilizata pentru monitorizarea pulsatiei de alunecare cu ajutorul monitorizarii curentilor statorici si folosind fluxul rotoric. Fluxul rotoric poate fi estimat in diferite moduri, de exemplu folosind ecuatiile (6.19) si (6.20). Aceste expresii contin fluxul statoric, care poate fi estimat din tensiunile si curentii statorici, cum s-a descris anterior. O alta cale este aceea de a reformula ecuatia (6.52) considerand expresia cuplului elecromagnetic data de ecuatia (4.9) scrisa astfel:
![]() .
.
Inlocuind ![]() din aceasta relatie, in ecuatia (6.51) -
dupa efectuarea calculelor - rezulta:
din aceasta relatie, in ecuatia (6.51) -
dupa efectuarea calculelor - rezulta:
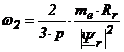 . (6.53)
. (6.53)
Expresia
contine modulul fluxului rotoric si de asemenea modulul cuplului electromagnetic.
Cuplul electromagnetic se poate de asemenea substitui prin ecuatia (2.97) ![]() , unde
, unde ![]() si
si ![]() sunt fluxurile
statorice in sistemul de referinta stationar si
monitorizarea lor a fost de asemenea discutata anterior. Este de asemenea
posibil sa se obtina o expresie pentru viteza rotorului
considerand ca din ecuatia (6.8) rezulta ca:
sunt fluxurile
statorice in sistemul de referinta stationar si
monitorizarea lor a fost de asemenea discutata anterior. Este de asemenea
posibil sa se obtina o expresie pentru viteza rotorului
considerand ca din ecuatia (6.8) rezulta ca:
![]() , (6.54)
, (6.54)
unde ![]() este viteza fluxului rotoric (fata de stator),
este viteza fluxului rotoric (fata de stator), ![]() si
si ![]() este pulsatia de
alunecare (data de exemplu de ecuatiile (6.52) si (6.53)). Cu
alte cuvinte
este pulsatia de
alunecare (data de exemplu de ecuatiile (6.52) si (6.53)). Cu
alte cuvinte ![]() este viteza
unghiulara a fazorului spatial al fluxului rotoric fata de
rotor. Este posibil sa se obtina o expresie pentru
este viteza
unghiulara a fazorului spatial al fluxului rotoric fata de
rotor. Este posibil sa se obtina o expresie pentru ![]() pe baza componentelor fluxului rotoric cu ajutorul
dezvoltarii derivatei
pe baza componentelor fluxului rotoric cu ajutorul
dezvoltarii derivatei ![]() . Deoarece fazorul spatial al fluxului rotoric exprimat
in sistemul de referinta stationar, fix, este:
. Deoarece fazorul spatial al fluxului rotoric exprimat
in sistemul de referinta stationar, fix, este:
![]() ,
,
atunci ![]() si urmeaza
ca:
si urmeaza
ca:

Numitorul
contine ![]() . Substituind ecuatia (6.55) in ecuatia (6.54)
si considerand (6.52) sau (6.53) in final obtinem:
. Substituind ecuatia (6.55) in ecuatia (6.54)
si considerand (6.52) sau (6.53) in final obtinem:
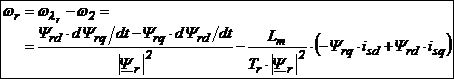 , (6.56)
, (6.56)
sau
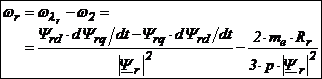 . (6.57)
. (6.57)
Se poate construi un estimator de viteza care monitorizeaza curentii statorici si componentele fluxului rotoric, care se pot obtine din componentele fluxurilor statorice cum s-a discutat anterior. Din ecuatia (5.4) se poate scrie:
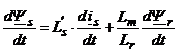 . (6.58)
. (6.58)
Pe de alta parte:
![]() . (6.59)
. (6.59)
Din ecuatiile (6.58) si (6.59) rezulta imediat:
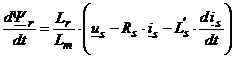 . (6.60)
. (6.60)
Conform
relatiei (6.59) fluxul statoric se obtine monitorizand curentii
statorici si monitorizand sau reconstruind, tensiunile statorice. O
implementare posibila, utilizand ecuatiile (6.60) si (6.56),
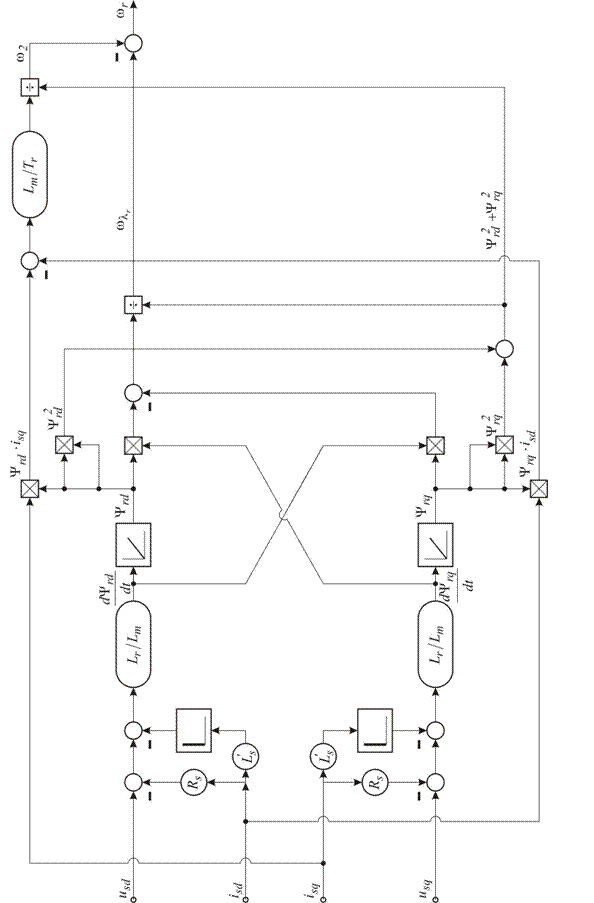
este prezentata in figura (6.10). Aceasta contine urmatorii trei
parametri ai masinii: ![]() ,
, ![]() si
si ![]() . Pentru implementarea digitala este posibil sa se
utilizeze diferite forme, inclusiv forma discreta [21]:
. Pentru implementarea digitala este posibil sa se
utilizeze diferite forme, inclusiv forma discreta [21]:
 , (6.61)
, (6.61)
unde ![]() .
.
![]()
Deoarece aceasta ecuatie contine
o eroare de modelare, care are drept rezultat o eroare a vitezei rotorice
estimate, pentru inlaturarea acestei erori, in practica, se poate
utiliza un filtru trece-jos. Trebuie observat ca intr-o actionare cu
orientare dupa camp, se poate obtine o estimare destul de
precisa a vitezei rotorului daca pulsatia de alunecare din
ecuatia (6.57) se inlocuieste cu valoarea sa de referinta
(impusa). De exemplu, intr-o actionare cu reglare dupa fluxul
rotoric (fig. 4.3) unde se utilizeaza valorile ![]() si
si ![]() ;
;
 sau
sau  .
.
Schema din figura (6.10) care foloseste ecuatiile (6.56) sau (6.57) este cea mai simpla si cea mai precisa.
Daca pentru a se obtine estimarile fluxului se utilizeaza tensiunile si curentii statorici, atunci prin considerarea variatiei termice a rezistentei statorice (de exemplu, prin folosirea unui model termic) si de asemenea prin folosirea inductivitatilor saturate potrivite, precizia estimarii se poate imbunatati mult. O actionare de reglare a cuplului (cu orientare dupa camp sau cu controlul direct al cuplului) fara senzori, de performanta ridicata, folosind acest tip de estimator de viteza va functiona cu succes chiar la viteze extrem de scazute (inclusiv viteza nula), daca estimatorul de flux este un observator in bucla inchisa.
|
Politica de confidentialitate |
| Copyright ©
2026 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |