Exemplu de implementare practica a circuitelor logice

Exemplu de implementare practica a circuitelor logice

Comparatie intre solutiile cu mintermeni si maxtermeni

In figura de mai jos sunt ambele solutii ale exemplelor din sectiunea precedenta, pentru comparatie:

Care solutie este mai simpla? Daca ar fi sa implementam fizic rezultatul sub forma de produs de sume, am avea nevoie de trei porti logice SAU si o poarta logica SI. Invers, daca ar fi sa implementam rezultatul sub forma de suma de produse, am avea nevoie de trei porti SI si o poarta SAU. In ambele situatii am avea nevoie de patru porti. Sa luam in considerare atunci si numarul de intrari ale portilor. Prima varianta utilizeaza 8 intrari, iar a doua 7 intrari. Din definitia costului minim, solutia sub forma sumei de produse este mai simpla. Acesta este un exemplu tehnic corect, dar care nu ne este de prea mare folos in realitate.

Solutia "corecta" depinde de complexitate si de familia de porti logice folosite. Solutia sumei de produse este mai buna faca folosim circuite TTL, a caror porti principale sunt portile SI-negat. Acestea sunt foarte bune pentru implementari sub forma de suma de produse. Pe de alta parte, solutia produsului de sume este acceptabila daca folosim circuite CMOS, deoarece avem astfel la dispozitie porti SAU-negat de toate marimile.

Echivalenta circuitelor SI-SAU cu circuitele SI-negat-SI-negat

Circuitele cu porti logice pentru ambele cazuri sunt prezentate mai jos, produsul de sume in stanga si suma de produse in dreapta:

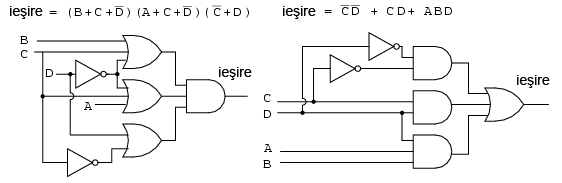
Reluam mai jos (stanga) circuitul sub forma sumei de produse:

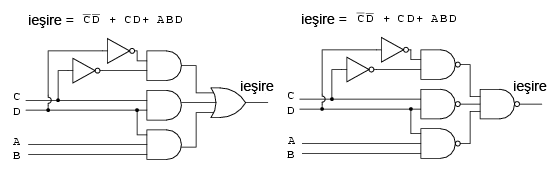
Daca inlocuim toate portile logice SI din stanga cu porti logice SI-negat, obtinem rezultatul din dreapta sus. Poarta SAU de la intrare este inlocuita de asemenea cu o poarta SI-negat. Pentru a demonstra ca logica SI-SAU este echivalenta cu logica SI-negat-SI-negat, este suficient sa mutam "cerculetele" inversoare de la iesirea celor trei porti SI-negat la intrarea portii finale SI-negat, conform figurii de mai jos:

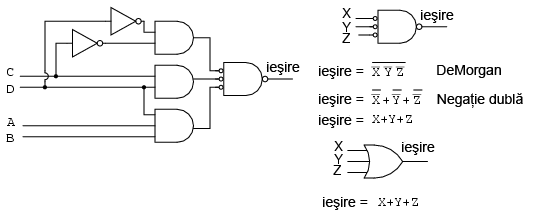
In figura de mai sus (dreapta), putem observa ca iesirea unei porti SI-negat cu intrari inversate este echivalenta din punct de vedere logic cu o poarta SAU, conform teoremei lui DeMorgan si a negatiei duble. Aceasta informatie ne este de ajutor in implementarea fizica a circuitelor digitale atunci cand dispunem de circuite logice TTL cu porti SI-negat.

Pasii necesari construirii logicii SI-negat-SI-negat in locul logicii SI-SAU, sunt urmatorii:

• Realizam un circuit logic (teoretic) sub forma de suma de produse
• Cand desenam diagrama logica, inlocuim toate portile logice (SI si SAU) cu porti logice SI-negat
• Intrarile nefolosite trebuie legate la valoarea logica "inalt"
• In caz de defect, nodurile interne de la primul nivel de iesire al portilor SI-negat nu sunt identice cu valorile diagramei SI-SAU, ci sunt inversate. Folosim diagrama logica SI-negat-SI-negat. Totusi, intrarile si iesirile finale sunt identice
• Notam fiecare capsula (circuit integrat) cu U₁, U₂, etc.
• Folosim catalogul producatorului pentru conectarea corecta a pinilor circuitului integrat la intrarile si iesirile portilor din circuit

Exemplu

Sa reluam o problema precedenta ce implica o simplificare sub forma sumei de produse. Vom realiza o simplificare sub forma unui produs de sume de aceasta data. Putem compara cele doua solutii la final.

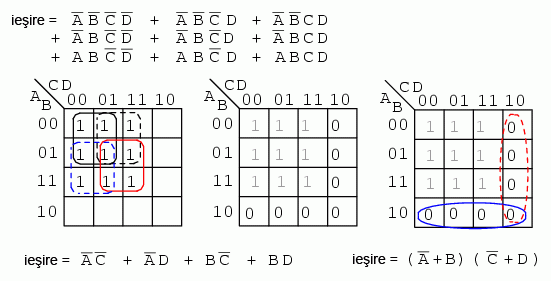
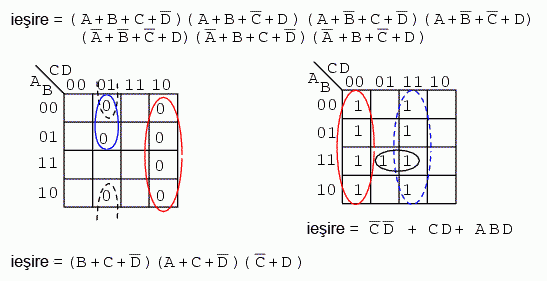
Solutie: in figura de sus stanga avem problema initiala, o expresie booleana cu 9 mintermeni nesimplificata. Recapituland, am format patru grupuri de cate patru regiuni fiecare. Rezultatul a fost o suma de patru produse (partea din stanga, jos).

In figura din mijloc, completam regiunile ramase libere cu valori de 0. Formam doua grupuri de cate patru regiuni. Grupul de jos (albastru) este A' + B, iar grupul din dreapta (rosu) este C' + D. Rezultatul este prin urmare un produs de doua sume, (A' + B)(C' + D).

Comparand cele doua solutii de mai sus, putem observa ca solutia produsului de sume reprezinta solutia cu cel mai mic cost. Pentru implementarea primei solutii am avea nevoie de 5 portii, iar pentru solutia produsului de sume am avea nevoie doar de 3. Folosind circuite logice TTL, aceasta din urma este si atractiva datorita simplitatii rezultatului. Putem gasim porti logice SI si SAU cu 2 intrari. Mai jos sunt prezentate circuitele logice pentru ambele solutii:

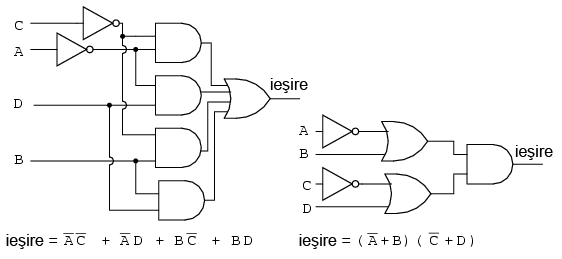
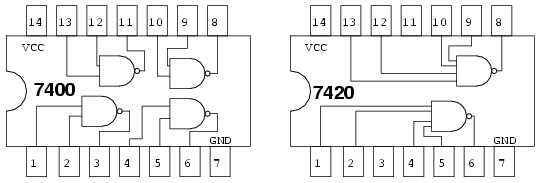
Sa presupunem ca avem la dispozitie circuitele logice TTL de mai jos. In acest caz, cunoastem si pozitionarea portilor logice in interiorul acestora, precum in figura de mai jos:

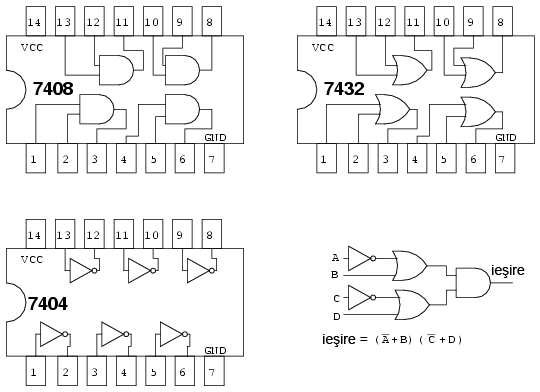
Circuitele integrate folosite (trei la numar) vor fi identificate prin notatia U1, U2 respectiv U3. Pentru a face distinctie intre portile individuale din fiecare capsula, acestea vor fi identificate prin a, b, c, d, etc. Circuitul inversor 7404 va fi U₁. Portile inversoare individuale sunt U1-a, U1-b, U1-c, etc. Circuitul SAU 7432 va fi notat cu U2, iar U3 este notatia folosita pentru circuitul SI 7408.

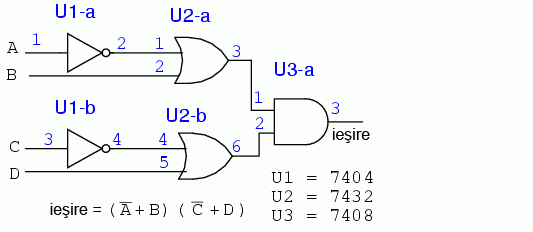
Luand in considerare piningul circuitelor logice folosite mai sus, vom desemna toate intrarile si iesirile circuitului logic ce vrem sa-l construim, conform figurii de mai jos (intrarile portilor nefolosite se vor lega la masa):

Putem gasi cu usurinta porti logice SI cu doua intrari (7408, stanga). Totusi, este mai greu sa gasim o poarta logica SAU cu patru intrari. Singurul tip de poarta cu patru intrari este un circuit TTL 7420 cu porti SI-negat (dreapta):

Putem transforma poarta logica SI-negat cu patru intrari intr-o poarta logica SAU cu patru intrari prin inversarea intrarilor acesteia:

Putem prin urmare folosi circuitul 7420 cu porti logice SI-negat cu patru intrari ca si poarta SAU prin negarea (inversarea) intrarilor.

Nu vom folosi porti logice inversoare discrete pentru inversarea intrarilor circuitului 7420. Vom folosi in schimb porti logice SI-negat cu doua intrari in locul portilor SI din solutia booleana cu mintermeni (suma de produse). Inversarea iesirii portilor SI-negat cu doua intrari este suficienta pentru inversarea necesara realizarii portii logice SAU cu patru intrari:

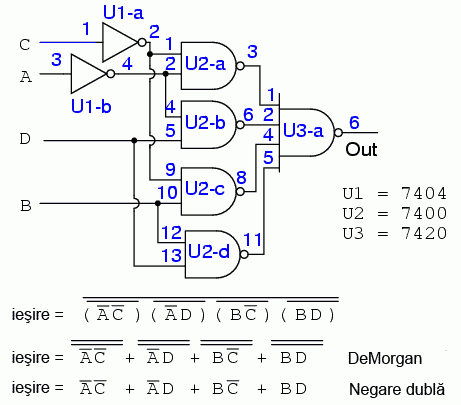
Rezultatul de mai sus este singura modalitate practica de realizarea a circuitului folosind TTL cu porti logice SI-negat-SI-negat in locul portilor SI-SAU.