Functii logice digitale
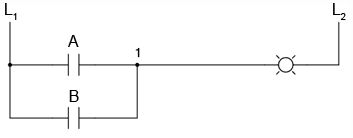
Putem construi functii logice simple pentru circuitul cu lampa din sectiunea precedenta, folosind contacte multiple. Documentarea acestor circuite se face relativ simplu prin conectarea unor linii aditionale diagramei initiale.
|
A |
B |
Iesire |
|
0 |
0 |
0 |
|
0 |
1 |
1 |
|
1 |
0 |
1 |
|
1 |
1 |
1 |
Daca folosim notatia binara standard pentru starea comutatoarelor si a lampii (0 pentru ne-actionat sau de-energizat, 1 pentru actionat sau energizat), putem utiliza un tabel de adevar pentru reprezentarea logicii circuitului.
Dupa cum se poate observa din diagrama ladder, lampa se va aprinde (energiza) in cazul in care contactul A sau contactul B este actionat. Electronii nu au nevoie decat de o singura cale (de la L1 spre 1) pentru a ajunge spre lampa. Prin urmare, indiferent care contact se inchide, A sau B, lampa se va aprinde.
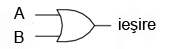
Ceea ce am implementat de fapt in acest caz nu este altceva decat o poarta logica SAU, utilizand doua contacte normal-deschise si o lampa.
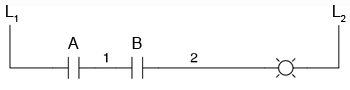
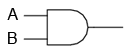
Putem imita functia unei porti logice SI prin conectarea celor doua contacte normal-deschise in serie si nu in paralel.
|
A |
B |
Iesire |
|
0 |
0 |
0 |
|
0 |
1 |
0 |
|
1 |
0 |
0 |
|
1 |
1 |
1 |
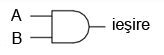
Putem verifica cu ajutorul tabelului de adevar ca acest lucru este intr-adevar corect.
In acest caz, lampa se va aprinde doar daca ambele contacte sunt actionate simultan. Curentul va putea trece de la L1 la 2 doar daca ambele contacte sunt inchise.

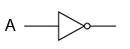
Functia logica de inversare poate fi obtinuta prin simpla utilizare a unui contact normal-inchis, fata de un contact normal-deschis precum cele folosite mai sus.
|
A |
Iesire |
|
0 |
1 |
|
1 |
0 |

Din nou, putem verifica prin intermediul tabelului de adevar ca acest lucru este corect.

Daca luam functia SAU prezentata mai sus si inversam fiecare intrare vom obtine functia SI-negat. Intrarile se inverseaza prin utilizarea contactelor normal-inchise in loc de contacte normal-deschise.
|
A |
B |
Iesire |
|
0 |
0 |
1 |
|
0 |
1 |
1 |
|
1 |
0 |
1 |
|
1 |
1 |
0 |

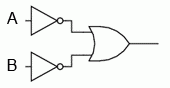
Lampa va fi energizata daca unul dintre contacte nu este actionat, si se va stinge doar daca ambele contacte sunt actionate simultan.
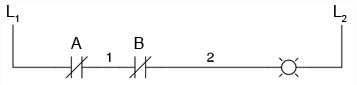
Asemanator, daca luam functia SI implementata mai sus, si inversam intrarile, obtinem functia logica SAU-negat. Inversarea intrarilor se realizeaza si in acest caz prin utilizarea contactelor normal-inchise in loc de contacte normal-deschise.
|
A |
B |
Iesire |
|
0 |
0 |
1 |
|
0 |
1 |
0 |
|
1 |
0 |
0 |
|
1 |
1 |
0 |


Din cele observate mai sus, putem trage unele concluzii, si anume: contactele paralele sunt echivalente cu o poarta logica SAU; contactele serie sunt echivalente cu o poarta SI; contactele normal-inchise sunt echivalente cu o poarta NU (negare).

Putem construi circuite logice combinationale prin gruparea contactelor in aranjamente serie-paralel. In exemplul alaturat, functia SAU-exclusiv este construita prin combinarea portilor SI, SAU si NU.
|
A |
B |
Iesire |
|
0 |
0 |
0 |
|
0 |
1 |
1 |
|
1 |
0 |
1 |
|
1 |
1 |
0 |

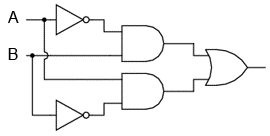
Linia de sus (contactul normal-inchis A in serie cu, contactul normal-deschis B) este echivalenta cu partea de sus a combinatiei de porti logice NU/SI. Linia de jos (contactul normal-deschis A in serie cu, contactul normal-inchis B) este echivalenta cu partea de jos a combinatiei de porti NU/SI. Conexiunea in paralel a celor doua linii in punctul 2, formeaza un circuit echivalent SAU. Acest lucru permite energizarea lampii fie prin linia 1 fir prin linia 2.
Pentru realizarea functiei SAU-exclusiv a trebuit sa folosim doua contacte pe o singura intrare: un contact pentru intrarea directa, iar celalalt contact pentru intrarea inversata. Cele doua contacte A din diagrama de mai sus sunt actionate fizic de acelasi mecanism. Acelasi lucru este valabil si pentru contactele B. Aceasta legatura "fizica" dintre contacte este scoasa in evidenta prin marcarea identica a contactelor. Nu exista nicio limita a numarului de contacte ce pot fi reprezentate pe acelasi releu. Fiecare nou contact adaugat unui releu sau unui comutator, fie ca este contact normal-inchis sau normal-deschis) este reprezentat prin acelasi simbol.
In unele situatii, se foloseste o marcare compusa de genul "A-1" si "A-2" in loc de "A" pentru ambele contacte ale aceluiasi dispozitiv. Acest lucru este folositor mai ales in cazul in care dorim sa scoatem in evidenta care seturi de contacte, din fiecare dispozitiv, este utilizat pentru care parte a circuitului. Pentru simplitate insa, nu vom folosi o asemenea notatie in cele ce urmeaza. Daca vedeti mai multe contacte marcate identic (A, B, etc.), puteti sa fiti siguri ca acele contacte sunt actionate de acelasi mecanism.
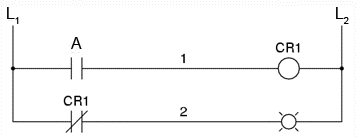
Daca dorim sa inversam iesirea unei functii logice realizate cu ajutorul unui comutator, trebuie sa folosim un releu cu un contact normal-inchis. De exemplu, daca vrem sa energizam o sarcina bazandu-ne pe negarea (functia NU) unui contact normal-deschis, putem realiza diagrama alaturata.
|
A |
CR1 |
Iesire |
|
0 |
0 |
1 |
|
1 |
1 |
0 |
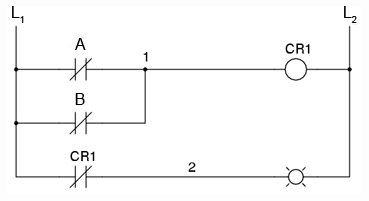
Releul este indicat pe figura prin notatia CR1 (releu de control 1). Atunci cand bobina releului, simbolizata printr-un cerc pe prima linie, este energizata, contactul de pe linia a doua se deschide. Deschiderea acestui contact de-energizeaza lampa. De la comutatorul la bobina CR1, functia logica este ne-inversata. Contactul normal-inchis este actionat de bobina releului CR1, asigurand o functie logica de negare (NU) pe lampa, inversa fata de starea de actionare a comutatorului (A).
Sa aplicam aceasta strategie de inversare uneia dintre functiile cu intrare inversata realizate mai sus. Spre exemplu, functia logica SI folosind diagrama functiei SI-negat de mai sus. Putem inversa iesirea cu ajutorul unui releu pentru realizarea unei functii ne-inversate.
|
A |
B |
Iesire |
|
0 |
0 |
0 |
|
0 |
1 |
0 |
|
1 |
0 |
0 |
|
1 |
1 |
1 |

De la comutator la bobina CR1, functia logica realizata este cea a unei porti SI-negat. Contactele CR1 normal-inchise inverseaza si transforma iesirea functiei SI-negat intr-o functie SI.
|
Politica de confidentialitate |
| Copyright ©
2025 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |