
Legea lui Ohm si teoremele lui Kirchhoff in forma complexa
Fie circuitul R, L, C serie prezentat anterior in figura 3.40 in
care tensiunea ![]() acopera
caderile de tensiune pe elementele de circuit:
acopera
caderile de tensiune pe elementele de circuit:
![]()
sau
![]()
Tinand seama de proprietatile numerelor complexe se poate transcrie relatia de mai sus, considerand valorile eficace ca marimi complexe:
![]() (84)
(84)
si apoi succesiv:

![]() . (85)
. (85)
Ultima relatie se numeste legea lui Ohm in forma complexa.
Expresia
![]() se numeste impedanta complexa a circuitului in
care R este rezistenta circuitului iar
se numeste impedanta complexa a circuitului in
care R este rezistenta circuitului iar ![]() este reactanta
circuitului.
este reactanta
circuitului.
Teoremele lui Kirchhoff prezentate la regimul electrocinetic se pot extinde si in regimul cvasistationar (regimul permanent sinusoidal, prescurtat c.a.):
 (86)
(86)
 (87)
(87)
notatiile folosite avand aceleasi semnificatii ca si cele utilizate in paragrafele 3.2.4 si anume:
k reprezinta o latura de circuit,
r un nod al circuitului electric iar
p un ochi al aceleiasi retele.
Relatia (86) exprima prima teorema a lui Kirchhoff in c.a.:
suma algebrica a valorilor instantanee a curentilor dintr-un nod electric este nula.
Relatia (87) exprima cea de a doua teorema a lui Kirchhoff in c.a.:
suma algebrica a valorilor instantanee ale tensiunilor electromotoare din laturile unui ochi electric ( bucla) este egala cu suma algebrica a caderilor de tensiune instantanee din laturile respective.
Aceasta exprimare nu se refera la bucle cuplate inductiv.
Transpuse in planul complex, relatiile (86) si (87) au forma:
 (88)
(88)
 . (89)
. (89)
Pentru exemplificare, aplicam aceste teoreme pentru nodul (fig. 30-a) si bucla (fig. 30 - b):
![]() si
si

 .
.
Prima teorema a lui Kirchhoff se aplica pentru (N_1) noduri, iar a II-a teorema, pentru B bucle independente, formandu-se un sistem de L ecuatii (L = N_1 +B ) unde L este numarul de laturi.
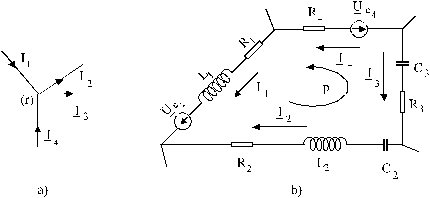
Fig. 30
|
Politica de confidentialitate |
| Copyright ©
2025 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |