Mintermeni si maxtermeni
Pana in acest moment am cautat solutii sub forma unei sume de produse la problemele de simplificare booleana. Pentru fiecare dintre aceste solutii exista o alta solutie sub forma unui produs de sume. Acest tip de solutie se poate dovedi a fi mai practica, in functie de aplicatie. Dar, inainte de a scrie solutiile sub forma unui produs de sume, trebuie sa introducem cateva concepte noi. Procedura de mai jos pentru extragerea termenilor sub forma de produs nu este noua. Vrem doar sa stabilim o procedura formala pentru mintermeni, ca mai apoi, sa putem face o comparatie cu noua procedura pentru maxtermeni.
Un mintermen este o expresie booleana rezultand intr-o valoare de 1 pentru iesirea unei singure regiuni dintr-o harta Karnaugh. Toate celelalte regiuni ale hartii Karnaugh sau ale tabelului de adevar fiind 0 in acest caz. Daca un mintermen contine un singur 1, iar regiunile ramase sunt toate 0, aria minima pe care acest mintermen o acopera este 1.
Figura de mai jos (stanga) prezinta mintermenul ABC, un singur termen sub forma de produs, ca si o singura valoare de 1 pe o harta Karnaugh unde toate celelalte regiuni sunt 0. Pana in acest moment, nu am prezentat valorile de 0 pe hartile Karnaugh considerate. Acestea se omit de obicei, exceptie facand cazurile speciale. Un alt mintermen, A'BC' este cel din dreapta. Ceea ce vrem sa subliniem este faptul ca adresa regiunii corespunde direct cu mintermenul extras de pe harta. Regiunea 111 corespunde mintermenului ABC din stanga. Regiunea 010 corespunde la randul ei mintermenului A'BC'. O expresie booleana sau o harta poate avea mai multi mintermeni.
Referindu-ne la figura de mai sus, putem scrie procedura introducerii unui mintermen pe o harta Karnaugh:
O expresie booleana este formata de cele mai multe ori din mai multi mintermeni, corespunzand mai multor regiuni pe o harta Karnaugh, precum in exemplul de mai jos:
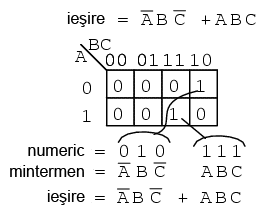
Mintermenii multiplii de pe aceasta harta sunt mintermenii individuali ce i-am analizat mai sus. Ceea ce vrem sa reamintim este faptul ca valorile de 1 sunt "traduse" de pe harta Karnaugh ca si o adresa binara transformata direct intr-unul sau mai multi termeni sub forma de produs. Prin direct, ne referim la faptul ca 0 corespunde unei variabile negate, iar 1 corespunde unei variabile "pure". De exemplu, 010 se transforma direct in A'BC'. In acest exemplu nu a existat nicio simplificare. Totusi, avem ca si rezultat o suma de produse prin intermediul mintermenilor.
Referindu-ne la figura de mai sus, putem rezuma pe scurt procedura de urmat in cazul simplificarii expresiei booleene sub forma unei sume de produse dintr-o harta Karnaugh:
Nimic nou pana in acest moment. Am scris doar pasii de urmat in cazul mintermenilor. Acelasi lucru il vom face si in cazul maxtermenilor.
Sa consideram acum o functie booleana ce este 0 pentru o singura regiune si 1 in rest:
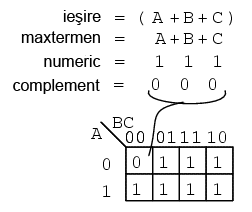
Un maxtermen este o expresie booleana a carei valoare este 0 pentru o singura regiune, toate celelalte regiunii ale hartii Karnaugh sau ale tabelului de adevar fiind 0. Vedeti si explicatia de la mintermen. Figura de sus stanga prezinta un maxtermen (A + B + C), o suma de trei termeni simplii. Pe harta, aceasta suma este reprezentata printr-un singur 0, toate celelalte regiunii ale hartii fiind 1. Daca un maxtermen are un singur 0, iar celelalte regiuni sunt 1, aria maxima pe care o acopera este 1.
Exista cateva diferente acum ca am introdus si maxtermenii. Maxtermenul este un 0, nu un 1 pe harta Karnaugh. Un maxtermen este un termen sub forma de suma, A + B + C in cazul nostru, si nu un termen sub forma de produs (ABC, de exemplu).
Pare ciudat ca locatia expresiei (termenului) (A + B + C) pe harta este 000. Pentru ecuatia "iesire = (A + B + C) = 0", toate cele trei variabile (A, B, C) trebuie sa fie egale cu 0. Doar expresia (0 + 0 + 0) = 0 va fi egala cu 0. Prin urmare, trecem singurul nostru maxtermen (A + B + C) in regiunea ce se afla la adresa A,B,C = 000 pe harta Karnaugh, unde toate intrarile sunt egale cu 0. Aceasta este singura posibilitate pentru a obtine valoarea de 0 pentru maxtermen. Toate celelalte regiuni contin valori de 1 pentru ca orice alte valori de intrare diferite de (0, 0, 0) pentru expresia (A + B + C) au ca si rezultat 1.
Luand in considerare figura de mai sus, pasii care trebuiesc urmati pentru introducerea unui maxtermen pe harta Karnaugh, sunt urmatorii:
Un alt maxtermen este prezentat in figura de mai jos. Valoarea numerica 000 corespunde termenului A' + B' + C'. Complementul este 111. Introducem o valoare de 0 pentru maxtermenul (A' + B' + C') la aceasta adresa (1, 1, 1) a hartii Karnaugh de mai jos:
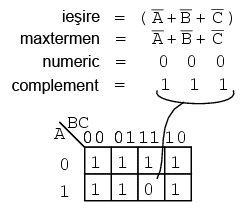
O expresie booleana sub forma produsului de sume poate avea mai multi maxtermeni, conform figurii de mai jos:
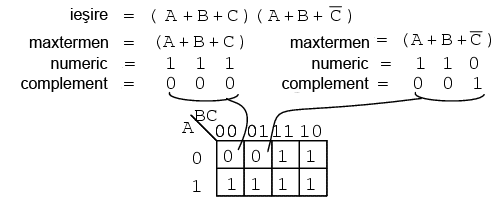
Maxtermenul (A + B + C) sub forma numerica este 111, iar complementat este 000. Plasam prin urmare un 0 la adresa (0, 0, 0). Maxtermenul (A + B + C') sub forma numerica este 110, iar complementat este 001. Plasam prin urmare un zero la adresa (0, 0, 1).
Acum ca am construit harta Karnaugh, suntem interesati de modul in care putem scrie o forma simplificata a expresiei booleene initiale sub forma de produs de sume. Primul pas este gruparea termenilor de 0, precum grupul de mai jos:
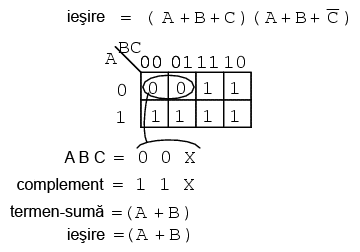
Scriem apoi valoarea binara corespunzatoare termenului-suma, ce arata astfel: (0, 0, X). Pentru grupul format, atat A cat si B sunt 0. Dar C este atat 0 cat si 1. Prin urmare, scriem un X in locul valorii lui C. Formam complementul: (1, 1, X). Scriem termenul suma (A + B) ignorand C-ul si X-ul ce l-a inlocuit.
Sa reluam pasii necesari pentru reducerea unei expresii booleene la un produs de sume:
Simplificati expresia booleana sub forma produsului de sume de mai jos. Scrieti rezultatul final sub forma unui produs de sume:
![]()
Solutie: completam o harta Karnaugh cu cei sapte maxtermeni de mai sus (introducem valori de 0). Retineti sa complementati variabilele de intrare pentru gasirea adresei corespunzatoare:
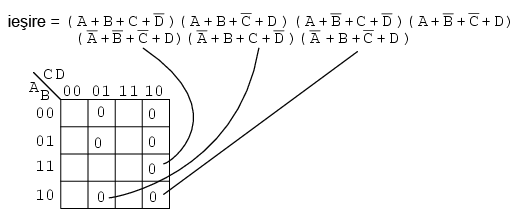
Dupa ce am introdus toti maxtermenii in tabel, trecem la gruparea regiunilor, precum in figura de mai jos. Grupurile mai mari se traduc printr-un termen-suma cu mai putine intrari. Cu cat avem mai putine grupuri, cu atat vom avea mai putin termeni-suma in expresia finala:
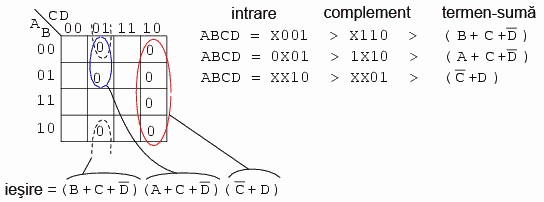
Avem trei grupuri, prin urmare, trebuie sa avem trei termeni-suma in rezultatul final. Detaliile simplificarii sunt prezentate in figura de mai sus. Pentru oricare grup, scriem mai intai adresa de intrare, o complementam si o transformam intr-un termen boolean sub forma de suma. Rezultatul final este produsul acestor trei termeni-suma.
Simplificati expresia booleana sub forma de produs de sume de mai jos, exprimand rezultatul sub forma unei sume de produse:
![]()
Aceasta problema este identica cu cea anterioara, cu diferenta ca expresia simplificata se cere sub forma de suma de produse si nu sub forma de produs de sume.
Trecem maxtermenii (0) din expresia initiala pe harta Karnaugh de mai jos (stanga), exact ca in exemplul precedent:

Completam apoi toate celelalte regiuni ramase libere cu valori de 1 (dreapta sus).
Formam grupuri de 1 pentru toate regiunile ce contin valori de 1. Scriem apoi rezultatul simplificat sub forma sumei de produse, conform sectiunii precedente a acestui capitol. Acest lucru este identic problemei precedente:
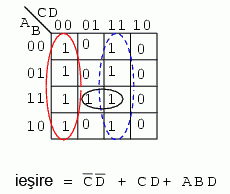
|
Politica de confidentialitate |
| Copyright ©
2025 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |