
Modele matematice pentru generatorul sincron
La baza construirii modelelor matematice pentru GS au stat ecuatiile lui Park din cadrul teoriei celei doua axe. Ecuatiile fundamentale ale masinii sincrone, in cadrul acestei teorii, se stabilesc pe baza urmatoarelor ipoteze fundamentale:
a) In axa longitudinala (d) se tine seama de influenta mutuala a trei circuite: statoric - d; de excitatie - E; de amortizare longitudinala - D (figura ).

Fig. Reprezentarea masinii sincrone trifazate in sistemul d,q.
In axa transversala (q) se tine seama de infleunta mutuala a doua circuite: statoric - q; de amortizare transversala - Q, fara sa se ia in considerare, pentru masina cu poli inecati, influenta masei de fier a rotorului pe axa q (figura 4.2).
b) In ecuatiile lui Park ale masinii sincrone se neglijeaza tensiunile electromotoare de pulsatie si rezistenta statorului, adica:

termeni care corespund variatiilor aperiodice si variatiilor sinusoidale armonice de rangul 2.
Aceasta neglijare este posibila deoarece componentele aperiodice se sting cu constante de timp foarte mici si nu prezinta importanta decat pentru defecte foarte apropiate din punct de vedere electric de masina sincrona, care sunt neinteresante pentru analiza comportarii masinii in cadrul unui sistem electro-energetic;
![]() c) Se
inlocuieste pulsatia cu w0 -
pulsatia sincrona; eroarea care se face prin
c) Se
inlocuieste pulsatia cu w0 -
pulsatia sincrona; eroarea care se face prin
aceasta aproximatie este cu atat mai mica cu cat masina se indeparteaza mai putin de turatia de sincronism. Aproximatia nu poate fi acceptata insa daca abaterile de la turatia de sincronism sunt mai mari de 5 %.
Cu aceste ipoteze si tinand seama de polarizarea infasurarilor descrisa in figura 4.2, se pot scrie urmatoarele ecuatii ale masinii sincrone corespunzatoare unui regim de functionare oarecare:
A. Ecuatii pentru axa longitudinala (d):
ecuatia electrica a statorului:
![]() (4.1)
(4.1)
ecuatiile electrice ale rotorului:

(4.2)
(4.3)
ecuatiile magnetice:
 (4.5)
(4.5)
(4.5)
(4.6)
B. Ecuatii pentru axa transversala (q)
ecuatia electrica a statorului
![]() (4.7)
(4.7)
ecuatia electrica a rotorului

(4.8)
ecuatiile magnetice

(4.9)
(4.10)
La aceste ecuatii de functionare pe cele doua axe si care descriu regimul electromagnetic se mai adauga:
C. Ecuatia de miscare a rotorului care descrie regimul electromecanic al masinii:

(4.11)
in care Cm - cuplul motor, Cc- cuplul electric rezistent si Tl - timpul de lansare raportat la puterea activa.
D. Ecuatia regulatorului de tensiune
![]()
(4.12)
E. Ecuatia regulatorului de viteza
![]() (4.13)
(4.13)
Deoarece setul de ecuatii (4.1) - (4.13) are un caracter teoretic general, inutilizabil practic, se impune modificarea formei de scriere a ecuatiilor pentru realizarea accesibilitatii practice a modelului, fapt ce conduce la considerarea, in regim tranzitoriu, a modelului elaborat de D.W. Olive.
1. Ecuatiile regimului tranzitoriu electromagnetic
1.1. Modelul Olive
![]() Pentru scrierea
ecuatiilor masinii sincrone in axa longitudinala (d) se
neglijeaza reactanta de scapari a
infasurarii de amortizare din axa longitudinala si
deci:
Pentru scrierea
ecuatiilor masinii sincrone in axa longitudinala (d) se
neglijeaza reactanta de scapari a
infasurarii de amortizare din axa longitudinala si
deci:
(4.14)
si in aceasta situatie, relatia (4.6) devine:
![]()
(4.15)
Notand cu:

(4.16)
(4.17)
(4.18)
(4.19)
 se pot scrie
succesiv egalitatile (4.20),(4.21):
se pot scrie
succesiv egalitatile (4.20),(4.21):
 Cunoscand, de
asemenea, ca:
Cunoscand, de
asemenea, ca:
adica:

(4.22)
si
![]()
![]() unde , deci ,
unde , deci ,
![]()
iar
 rezulta:
rezulta:
(4.23)
Prin transformari si inlocuiri succesive in relatiile (4.18)-(4.21) si punand ecuatiile (4.2) si (4.3) respectiv sub formele:

(4.24)
si
(4.25)
in urma schimbarii notatiilor se obtin "ecuatiile Olive" dupa axa longitudinala a masinii sincrone sub forma:

in care s-au notat:
constanta de timp a inductorului la mers in gol al masinii;

- constanta de timp a infasurarii de amortizare longitudinala;

- valoarea tensiunii de excitatie raportata la circuitul statorului.

Daca se elimina din primele trei ecuatii din (4.26), marimile Eq1, Eq2 si Id, si se substituie in celelalte doua ecuatii se obtin relatiile:

(4.27)
(4.28)
Aceste ecuatii determina variatia tensiunilor electromotoare E'q si E"q ce caracterizeaza regimul de functionare al masinii sincrone in axa longitudinala.
Procedand analog pentru axa transversala (q) si pe baza ipotezelor enuntate, se obtine ecuatia:

(4.29)

unde - constanta de timp a infasurarii de amortizare transversala.
Ecuatiile (4.27) - (4.29) descriu regimul tranzitoriu electromagnetic al masinii sincrone. Se observa ca pentru obtinerea regimului stationar este suficienta punerea conditiei:

rezultand:

(4.30)
iar din primele doua ecuatii (4.30) rezulta:

(4.30')
care sunt ecuatiile cunoscute ale regimului stationar al masinii sincrone.
2. Ecuatiile regimului tranzitoriu electromecanic
2.1. Ecuatia de miscare a rotorului
In categoria ecuatiilor regimului tranzitoriu electromecanic se includ: ecuatia de miscare a rotorului G.S. si ecuatiile SRAV (descrise deja in capitolul II).
Ecuatia de miscare a rotorului G.S. se obtine pornind de la ecuatia care exprima echilibrul cuplurilor care antreneaza rotorul G.S., si anume:

(4.31)
in care b w0t + d este unghiul
absolut format de axa rotorica cu axa fazei "a" de referinta
(fixa in timp si spatiu), conform figurii 4.3; J -
momentul de inertie al maselor in miscare;
Cm - cuplul mecanic la arborele rotoric; Ce - cuplul
electromagnetic. Daca se defineste:

(4.32)
![]()
unde - viteza unghiulara geometrica a axei de referinta si d = pg - unghiul electric
extern pentru o masina cu "p" perechi de poli, unghiul g format de axa, "q" cu axa de referinta va fi unghiul intern al masinii sincrone.

Fig.4.3. Pozitia momentana a rotorului G.S.
Cu notatiile anterioare, relatia (4.32) devine:

si efectuand derivata in raport cu timpul avem:

care inlocuita cu relatia (4.31) ne da:
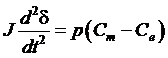
(4.33)
Relatia (4.33) reprezinta o forma de exprimare a ecuatiei de miscare. In functie de unitatile de masura folosite, in literatura de specialitate exista si alte forme de exprimare a ecuatiei de miscare conform celor prezentate in tabelul 4.1.
Tabelul 4.1. Alte forme de exprimare a ecuatiei de miscare a rotorului masinii sincrone.

In tabelul 4.1. s-au folosit notatiile:
w pf0= 314 rad/sec,
t [rad] = w0t [sec]

In general, cele mai des folosite sunt formele 6,7 si 8, forma 7 fiind folosita in special in analiza stabilitatii statice, in prezenta regulatoarelor.
Dar in regim tranzitoriu, in timpul oscilatiilor pronuntate ale rotorului, acceleratia unghiulara este mare si nu se mai poate neglija componenta asincrona a cuplului electromagnetic. Ca urmare, relatia de echilibru a cuplurilor va fi:
![]()
(4.34)
sau, sub forma explicita:

(4.35)
Inmultind relatia (4.35) cu W0 se poate trece de la "expresia in cupluri" la "expresia in puteri" stiind ca in general C W = P. Avem deci:
 (4.36)
(4.36)

Tinand seama de relatia dintre viteza unghiulara geometrica si cea electrica, si de faptul ca viteza relativa a rotorului este:

(4.37)
rezulta:

sau notand cu - constanta mecanica a rotorului, putem scrie:
 (4.38)
(4.38)
care reprezinta ecuatia de miscare a rotorului in regim tranzitoriu. Ecuatia se mai poate scrie in u.r. daca se defineste timpul de lansare ca fiind:


(4.39) si constanta de amortizare: (4.40)
Relatia (4.38) va deveni, in aceasta situatie:

(4.41)
 adica, in
u.r.:
adica, in
u.r.:
(4.41')
Deoarece integrarea acestei ecuatii diferentiale de ordinul 2 este dificila, ea se transforma in doua ecuatii diferentiale de ordinul intai si anume:

(4.42)
cele doua ecuatii diferentiale (4.42) reprezentand ecuatiile miscarii rotorului masinii sincrone in regim tranzitoriu, la care se adauga ecuatiile SRAV.
3. Considerarea fenomenelor din miezul feromagnetic al masinii sincrone
Principalele fenomene pe care le introduce miezul feromagnetic sunt: histereza, aparitia curentilor turbionari si saturatia. Considerarea distincta a acestor fenomene este deosebit de dificila deoarece ele sunt neliniare si caracterizate prin relatii foarte complexe care necesita calcule laborioase. Neglijarea lor insa duce de multe ori la conditii mai grele pentru stabilitate, mai ales in cazul unei analize a stabilitatii dinamice pe termen lung.
3.1. Histereza
Efectele mai importante datorate histerezei magnetice la generatorul sincron sunt:
prezenta unui flux remanent in intrefier in lipsa curentului de excitatie;
existenta unei relatii neliniare intre fluxul din intrefier si curentul de excitatie;
aparitia unor cupluri suplimentare;
existenta unui defazaj intre fluxul din intrefier si tensiunea magnetomotoare.
Histereza se poate lua in considerare prin modelarea a doua infasurari rotorice, cate una pe fiecare axa (d) si (q), care sa fie parcurse de curenti dependenti de fluxul dupa axa respectiva, conform dependentei rezultate din curba de histereza determinata pentru curentul respectiv. Parametrii celor doua infasurari (R si X) se determina in asa fel incat pierderile in aceste infasurari sa fie identice cu pierderile prin histereza in cazul magnetizarii alternative a rotorului si sa reproduca defazajul necesar pentru a se obtine forma dorita a curentului. Infasurarile se considera alimentate cu surse de putere infinita pentru ca modificarea curentilor ce le strabat sa fie dependenta de fluxul rezultant dupa o lege bine determinata.
Dar, din cauza intrefierului care preia cea mai mare putere din tensiunea magnetomotoare, efectul histerezei este foarte redus si deci, se poate neglija in cele mai multe din cazurile practice, inclusiv intr-o analiza de dinamica pe termen lung.
3.2. Curentii turbionari
In generatorul sincron, curentii turbionari apar atat in stator cat si in rotor. In stator, ei se manifesta atat la functionarea in regim tranzitoriu cat si in regim stationar. In regim tranzitoriu, la campul invartitor cu amplitudine constanta din regimul stationar se adauga si variatia in timp a amplitudinii campului. Dar aceasta nu este mai rapida decat variatia obisnuita a campului datorita rotatiei, efectul suplimentar dat de curentii turbionari statorici, in procesul tranzitoriu, fiind neglijabil fata de regimul stationar. In rotor, in regim tranzitoriu, fluxul rotoric variaza in timp, deci apar curenti turbionari, pe cand in regim stationar, datorita constantei fluxului, acestia sunt nuli.
Prezenta curentilor turbionari are ca efecte:
aparitia unor pierderi suplimentare in fierul rotoric;
aparitia unor cupluri de amortizare asemanatoare celor produse de infasurarea de amortizare;
modificarea valorii fluxului in intrefier ca modul si faza.
Efectul curentilor turbionari este important la functionarea generatorului sincron in sarcina capacitiva, in regim asincron datorita pierderii excitatiei, in procesul autosincronizarii si in studiul influentei reglajelor.
Deoarece considerarea riguroasa a curentilor turbionari nu se poate face decat scriind ecuatiile lui Maxwell pentru circuitele pe care acestia le strabat, tinand seama de forma constructiva a generatorului sincron, iar solutionarea ecuatiilor obtinute conduce la un mare volum de calcule se propune considerarea curentilor turbionari printr-o echivalenta a efectelor pe care acestia le produc. Se prezinta, in acest sens, in principiu, patru moduri de luare in considerare a curentilor turbionari si anume:
a) scriind impedantele operationale ale generatorului sincron Xd(s) si Xq(s) si tinand cont de curentii turbionari din miezul feromagnetic. In acest sens se propune inlocuirea sistemului de ecuatii (3.27) - (3.29) cu sistemul de ecuatii operationale de forma:

(4.43)
 unde:
unde:
![]()
iar termenul se aproximeaza prin:
 (4.44)
(4.44)
in care a b g, T1 si T2 sunt constante ce se determina din caracteristica de frecventa a generatorului sincron ridicata intr-un regim asincron.
b) Introducerea de infasurari suplimentare de amortizare (dupa cele doua axe (d) si (q), in cuadratura) corespunzatoare curentilor turbionari. Aici se pune problema stabilirii numarului de infasurari, astfel ca pe fiecare axa sa existe cate o infasurare pentru fiecare cale de inchidere a curentilor turbionari si cate o infasurare pentru curentii statorici si respectiv, cei rotorici, iar determinarea parametrilor electrici ai infasurarilor curentilor turbionari sa se faca astfel incat caracteristicile de frecventa ale generatorului sincron real si a celui echivalent sa fie cat mai apropiate. S-a constatat in acest sens, ca daca masina este nesaturata, raportul parametrilor acestor infasurari este R/X=1, iar daca este saturata, raportul devine R/X=2.
 Dar deoarece
statorul este confectionat din tole, constanta de timp echivalenta
curentilor turbionari este foarte mica si astfel, efectul lor
dispare practic instantaneu. In schimb in rotor, care este confectionat
masiv, curentii turbionari indusi pot fi mari, iar contributia
lor este semnificativa in regim tranzitoriu. De aceea, in calcule sunt
cuprinsi in majoritatea cazurilor numai curentii turbionari rotorici,
iar reprezentarea efectului lor, cea mai comoda pentru ecuatiile
masinii, este reprezentarea prin infasurari echivalente
scurtcircuitate dupa fiecare din cele doua axe (d) si (q). In
acest caz, la setul de ecuatii (4.1)-(4.10) se mai adauga
ecuatiile:
Dar deoarece
statorul este confectionat din tole, constanta de timp echivalenta
curentilor turbionari este foarte mica si astfel, efectul lor
dispare practic instantaneu. In schimb in rotor, care este confectionat
masiv, curentii turbionari indusi pot fi mari, iar contributia
lor este semnificativa in regim tranzitoriu. De aceea, in calcule sunt
cuprinsi in majoritatea cazurilor numai curentii turbionari rotorici,
iar reprezentarea efectului lor, cea mai comoda pentru ecuatiile
masinii, este reprezentarea prin infasurari echivalente
scurtcircuitate dupa fiecare din cele doua axe (d) si (q). In
acest caz, la setul de ecuatii (4.1)-(4.10) se mai adauga
ecuatiile:
Dupa axa (d): (4.45)

Dupa axa (q): (4.46)
iar ecuatiile magnetice (4.4) - (4.6), respectiv (4.9) si (4.10) devin:

(4.47)
Se observa ca prezenta curentilor turbionari va determina incetinirea oricarei variatii a fluxului magnetic.
Cat priveste caracteristicile infasurarilor echivalente curentilor turbionari, in literatura de specialitate se dau urmatoarele valori:
- Infasurarile echivalente se caracterizeaza prin cos j = 0,894 si R/X=2;
- Se da unghiul de defazaj .
- Se dau cos j = 0,707 in teoria liniara si cos j 0,895) in teoria limita.
- Se precizeaza ca dispersia infasurarii este de (16,66-33)%.
c) Daca se considera numai curentii turbionari din rotor, problema modelarii efectului lor poate fi privita si dintr-un alt unghi de vedere, si anume: infasurarile suplimentare prin care se modeleaza efectul curentilor turbionari se pot considera ca infasurari suplimentare de amortizare care vor introduce in ecuatia de miscare un termen suplimentar proportional cu alunecarea rotorului. In acest caz, pe baza relatiei de calcul a pierderilor de putere datorate curentilor turbionari se determina expresia cuplului suplimentar de amortizare care intervine in ecuatia de miscare sub forma:
Pentru turbogeneratoare:

(4.48)
Pentru hidrogeneratoare:

(4.49)


unde pentru o inductie B = 1 T; iar , alunecarea.
Relatiile (4.48) si (4.49) sunt deosebit de avantajoase pentru modelarea efectului curentilor turbionari. Deoarece cuplul suplimentar de amortizare este proportional cu patratul inductiei magnetice rezultante, iar in procesele tranzitorii, inductia magnetica poate fi considerata proportionala cu t.e.m. tranzitorie dupa axa (q), adica E'q si relatiile se mai pot scrie:

(4.50)
(4.51)
fapt ce permite calculul cuplului suplimentar de amortizare creat de curentii turbionari la fiecare pas de calcul al procesului de analiza a regimului tranzitoriu cunoscandu-se valoarea lui E'q. Trebuie remarcat faptul ca este necesara introducerea valorilor cuplurilor suplimentare CtT si CtH cu semnul alunecarii in expresia ecuatiei de miscare a rotorului datorita caracterului lor amortizant atat la accelerarea cat si la decelerarea rotorului masinii sincrone. De asemenea, cunoscand si frec-venta la fiecare pas de calcul se poate determina puterea amortizanta data de curentii turbionari:
![]()
(4.52)
iar cu aceasta, sistemul de ecuatii (4.42), in u.r. care descriu comportarea in regim tranzitoriu a masinii sincrone pe canalul electromecanic devine:

(4.53)
in care ptr - reprezinta puterea amortizanta a curentilor turbionari exprimata in u.r. fata de puterea de baza, Sb - aleasa pentru SEE considerat.
Cat priveste valorile constantelor AT si AH din relatiile (4.50) si (4.51) acestea se calculeaza in functie de sistemul de unitati folosit. Astfel, pentru inductia de 1T la 50 Hz si o suprafata a fierului de 1 m2, in conditiile unui raport normal intre t.e.m. polara, Eq si t.e.m. tranzitorie, E'q de: Eq/ E'q =1,66 1,75, valorile sunt:
![]()
![]()
si
Modelul prezentat mai sus nu afecteaza ecuatiile canalului electromagnetic al masinii sincrone si nici parametrii electrici ai acesteia.
d) Al patrulea mod de considerare a curentilor turbionari ar fi prin marirea rezistentei infasurarilor statorice pentru ca pierderile rezultante prin efect Joule Lenz sa acopere si pierderile prin curenti turbionari.
3.3. Saturatia
In studiile de stabilitate tranzitorie, tratarea simplificata a generatorului sincron presupune neglinarea saturatiei, fapt ce dauneaza preciziei rezultatelor obtinute pe cale teoretica fata de cele experimentale. In analiza dinamicii pe termen lung a unui sistem de generatoare sincrone interconectate luarea in considerare a saturatiei este obligatorie datorita extinderii scalei timpului de analiza fapt ce permite manifestarea efectelor acesteia.
Efectele saturatiei sunt, in principal, urmatoarele:
modificarea formei campului magnetic din intrefier fata de o sinusoida;
modificarea intrefierului echivalent;
dependenta caracteristicii de magnetizare de infasurarea care produce campul magnetic;
decalarea axei magnetice a polilor campului datorita influentei reactiei transversale a indusului;
- deformarea curbei curentului in timp.
De asemenea, saturatia influenteaza comportarea generatorului sincron in conditiile considerarii reglajului automat de tensiune si a functionarii pe o sarcina capacitiva.
Luarea in considerare a saturatiei face ca inductivitatile generatorului sincron sa nu mai fie constante, ci sa se modifice dependent de valoarea curentilor din diferitele infasurari ale masinii. Modificarea valorii inductivitatilor este determinata de dependenta neliniara dintre inductia magnetica B si intensitatea campului magnetic H. In literatura, curba reala B = f(H) este aproximata prin curbe continue, prin una, doua sau mai multe portiuni de dreapta de m = const. sau printr-un polinom de ordinul n, unde n = 8 10, de forma:
![]()
(4.54)
unde y - fluxul in intrefier si x- tensiunea magnetomotoare rezultanta sau obtinuta printr-o formulare numerica.
Luarea in considerare a saturatiei se poate face in mai multe feluri. Daca insa se utilizeaza modelul liniarizat al generatorului sincron se impune introducerea saturatiei sub forma unor corectii aduse valorilor reactantelor de reactie Xad si Xaq prin intermediul unui coeficient de saturatie kSAT sau a unei functii de saturatie fSAT.
Daca se utilizeaza metoda coeficientului de saturatie trebuie admise urmatoarele ipoteze:
- reactanta de dispersie este constanta si independenta de saturatie, fluxul de dispersie inchizandu-se mai mult prin aer;
- saturatia se determina din fluxul rezultant din intrefier, acelasi pentru aceeasi t.m.m. rezultanta, in sarcina sau la mers in gol;
- dependenta dintre t.e.m. in intrefier, Uδ si solenatia totala (curent de excitatie si curenti de reactie stator) este data de caracteristica de mers in gol;
- rotorul este cilindric (are poli plini).
Coeficientul de saturatie se defineste ca fiind:
(4.55)
La masinile cu poli aparenti din cauza intrefierului mare dupa axa (q), reactanta utila dupa axa (q) se considera constanta, neafectata de saturatie.
Deci:

(4.56)
La masinile cu poli inecati se afecteaza ambele reactante, de saturatie. In acest scop se va considera un flux rezultant , cu ajutorul caruia, din caracteristica de magne-
tizare se obtine valoarea saturata a reactantei, prin intermediul coeficientului de saturatie:
![]()
(4.57)
![]() Daca se
utilizeaza, metoda functiei de saturatie, fSAT aceasta se
poate exprima sub forma:
Daca se
utilizeaza, metoda functiei de saturatie, fSAT aceasta se
poate exprima sub forma:
(4.58)
care se stabileste cu ajutorul curbei de saturatie in gol (data de fabrica constructoare) si care exprima dependenta dintre tensiunea la borne (sau E'q) si curentul de excitatie.
 Marimile se
exprima in u.r., valorile de referinta fiind tensiunea
nominala si curentul de excitatie de baza (sau mai
convenabil, t.e.m. EI corespunzatoare curentului de excitatie
de baza).
Marimile se
exprima in u.r., valorile de referinta fiind tensiunea
nominala si curentul de excitatie de baza (sau mai
convenabil, t.e.m. EI corespunzatoare curentului de excitatie
de baza).
Fig.4.4. Utilizarea curbei de saturatie pentru determinarea parametrilor A si B.
Se defineste, de asemenea, parametru:
![]()
(4.59)
legat de fSAT prin relatia:

(4.60)
Constantele si din relatia (4.59) sunt valorile lui EI calculate fara considerarea efectului saturatiei.
In figura 4.4. se reprezinta modul in care curba de saturatie, etalonata in u.r. se foloseste la determinarea parametrilor A si B.
Desi metoda functiei de saturatie fSAT este simpla si eleganta se considera ca este dificila cunoasterea exacta a curbelor de saturatie pentru fiecare masina sincrona din SEE. De asemenea este greu de cunoscut si caracteristicile de mers in gol ale generatoarelor. De aceea, pentru a lua in considerare saturatie se utilizeaza metoda coeficientilor de saturatie calculati dupa axele d si q, in mod analitic si bazandu-se pe urmatoarele ipoteze suplimentare:
gradul de saturatie dupa o axa este proportional cu componentele tensiunii din spatele reactantei de dispersie;
deformarea fluxului din intrefier nu schimba valorile inductivitatii nesaturate sau nu distruge variatia sinusoidala a inductivitatii rotorului si statorului.
In aceasta situatie, coeficientii de saturatie se obtin analitic din relatiile (4.61), (4.62):


(4.62)
In aceasta situatie, ecuatiile canalului electromagnetic al generatorului sincron, in regim tranzitoriu, cu considerarea saturatiei, devin:

in care X - reactanta de dispersie statorica
Ud, Uq - proiectiile dupa axele (d) si (q) ale tensiunilor din spatele reactantelor de dispersie.
Tensiunea aleasa pentru a fi folosita in spatele reactantei tranzitorii X'd se exprima prin componentele sale dupa axele (d) si (q) astfel:

(4.64)
sau, cu considerarea saturatiei, relatiile (4.64) devin:

(4.65)
Ecuatiile (4.27), (4.28) , (4.29) setul de ecuatii (4.63)-(4.65) si ecuatiile (4.50)-(4.53) formeaza sistemul general de ecuatii care descriu comportarea in regim tranzitoriu a generatorului sincron cu luarea in considerare a fenomenelor din miezul feromagnetic. Acest sistem general de ecuatii, la care se vor adauga ecuatiile ce descriu influenta reglajelor de tensiune si de viteza, va sta la baza determinarii unui model concret pentru generatorul sincron in regim tranzitoriu.
4. Ecuatiile G.S. in regim dinamic al SEE
In regimul dinamic al SEE care urmeaza procesului tranzitoriu electromagnetic si electromecanic si este cauzat de actiunea perturbatoare a sistemelor de reglare lente ale instalatiilor primare din centrale, GS nu necesita o reprezentare prea detaliata, contributia lor la desfasurarea procesului dinamic fiind redusa, comparativ cu aceea data de instalatiile termo si hidromecanice. Totusi fiind vorba de un proces dinamic este bine ca modelul G.S. sa pastreze in principiu, caracterul regimului tranzitoriu mai ales datorita faptului ca in acest interval de timp tensiunea si frecventa se pot modifica in limite largi.
4.1. Modelul matematic al G.S. pe canalul electromagnetic.
4.1.1. Modelul Stagg-El-Abiad
Acest model a fost conceput pentru studii de stabilitate de foarte scurta durata (sub o secunda) cand nu intereseaza reprezentarea detaliata a fenomenelor electromagnetice din masina sincrona. Dar pentru ca si in procesele DTL, se pune aceeasi problema, modelul poate fi bine adaptat si pentru reprezentarea G.S. in procesele dinamice care depasesc 3-4 secunde. In acest caz G.S. poate fi reprezentat simplu printr-o sursa de tensiune electromotoare in spatele reactantei tranzitorii, ca in figura 4.5. Aceasta tensiune este constanta ca valoare, dar isi modifica pozitia fata de o axa de referinta aleasa arbitrar. Tensiunea din spatele reactantei tranzitorii se determina din:
![]()
(4.66)

Fig.4.5. Reprezentarea simpla a G.S.
![]() Considerand
actiunile fluxurilor de-a lungul celor doua axe in cuadratura,
"d" si "q", se poate calcula o tensiune fictiva dupa axa "q" in
spatele reactantei sincrone Xq dupa aceasta axa.
Considerand
actiunile fluxurilor de-a lungul celor doua axe in cuadratura,
"d" si "q", se poate calcula o tensiune fictiva dupa axa "q" in
spatele reactantei sincrone Xq dupa aceasta axa.
(4.67)
Fluxul sinusoidal produs de curentul de excitatie actioneaza de-a lungul axei "d". Tensiunea indusa de acesta ramane in urma fluxului cu p/2 grade electrice si se afla in axa "q". Aceasta tensiune electromotoare poate fi determinata adaugand la tensiunea la borne, caderea de tensiune pe rezistenta infasurarii statorice si caderea de tensiune reprezentand efectele demagnetizante dupa axele "d" si "q". Neglijand saturatia avem:
![]()
(4.68)
in care EI -este t.e.m. proportionala cu curentul de excitatie.
In figura 4.6 se reprezinta diagrama fazoriala corespunzatoare t.e.m. EI. Pe baza ei se poate calcula t.e.m. E'q proportionala cu inlantuirea fluxului de excitatie, care rezulta prin combinarea efectelor curentului de excitatie si a curentilor statorici. Variatia lui E'q in lungul axei "q" este dependenta de t.e.m. de excitatie (controlata de actiunea RAT) si de t.e.m. proportionala cu curentul de excitatie, EI si invers proportionala cu constanta de timp tranzitorie la mers in gol.

(4.69)
Relatiile (4.67) - (4.69) descriu modelul matematic al G.S. pentru regimurile tranzitorii rapide cu durata mai mica de 1 secunda, pe canalul electromagnetic.

Diagrama fazoriala corespunzatoare t.e.m. EI. si E'q
4.1.2. Ecuatiile G.S. pe canalul electromagnetic, in regim dinamic
Pentru descrierea matematica a functionarii G.S. pe canalul electromagnetic se impune luarea in considerare a fenomenelor din fierul masinii in scrierea ecuatiilor sale. Dar regimul dinamic considerat are o dinamica foarte lenta din unghiul de vedere al marimilor electromagnetice ale G.S. el fiind calat pe dinamica instalatiilor primare care, asa cum s-a vazut au temporizare mare. Ca urmare, fenomenele din fierul masinii sincrone pot fi considerate cele corespunzatoare regimului stationar cu mentiunea ca daca saturatia se modeleaza printr-un coeficient de saturatie care modifica reactanta G.S., trebuie sa se tina seama si de modificarea acesteia cu frecventa SEE. Pentru a evita aceasta se prefera reprezentarea saturatiei prin functia de saturatie, fSAT, descrisa la paragraful 3.3. (relatia 4.58), care, pentru o curba universala de magnetizare poate lua, in u.r., forma liniara:
![]()
(4.70)
In aceasta situatie, relatia (4.69) devine:

(4.71)
iar modelul G.S. pe canalul electromagnetic in regim dinamic se poate construi dupa un algoritm care tine seama si de includerea G.S. in modelul retelei electrice pentru determinarea circulatiei de puteri in regim dinamic.
La baza acestui algoritm a stat ideea introducerii unei noi marimi de calcul, tem E' considerata ca fiind o marime inertiala (care nu se modifica brusc), adica constanta de-a lungul unui pas de calcul.
Aceasta permite reprezentarea simpla a G.S. prin tem E' de calcul in spatele impedantei cores-punzatoare, conform figurii 4.5, in vederea rezolvarii circulatiei de puteri. Pentru calculul tem E' s-a reprezentat in figura 4.7. diagrama fazoriala a G.S. in regim stationar.
Trebuie precizat faptul ca prin reprezentarea G.S. ca o t.e.m.in spatele unei impedante, in reteaua electrica se introduce cate un nou nod, corespunzator fiecarui G.S. Dar pentru ca tem E' a fiecarui G.S. este cunoscuta ca modul si faza la fiecare pas de calcul, noul nod introdus in retea este de tip balansare (echilibrare) si nu intervine la calculul iterativ al tensiunilor in noduri.
Matricea de admitanta nodala, insa, trebuie augmentata cu impedanta de legatura care apare intre noile noduri (ale tem E') si retea.

Fig.4.7. Diagrama fazoriala a G.S. pentru regim stationar.
Algoritmul reprezentarii G.S. pe canalul electromagnetic, in regimul dinamic al SEE si, implicit, al determinarii t.e.m. de calcul E' este urmatorul:
la fiecare pas de calcul si pentru fiecare nod:
A1: daca nodul nu este de tip generator se trece la A14;
A2: cunoscand puterea activa si reactiva debitate si tensiunea la borne, de la pasul anterior, se calculeaza componentele activa si reactiva ale curentului de sarcina:

(4.72)
A3 : se determina unghiul de sarcina al G.S.:

(4.73)
A4: se calculeaza unghiul intern al masinii sincrone:

(4.74)
A5: se calculeaza unghiul total:
![]() (4.75)
(4.75)
se determina t.e.m. polara dupa axa "q", E4, in modul pe baza unui calcul de circulatie de curent pe impedanta sincrona:

(4.76)
A7: se calculeaza valoarea curentului de sarcina total si a componentelor dupa axele d si q ale curentului, cu relatiile:

(4.77)
A8: se determina valoarea t.e.m., EI, corespunzatoare curentului total:

(4.78)
A9: se considera interventia SRAT care va determina valoarea t.e.m. Efd corespunzatoare campului de excitatie;
A10: se determina valoarea componentei dupa axa q a t.e.m. tranzitorii E' tinandu-se seama de saturatie:

(4.79)
A11: daca G.S. considerat nu are infasurari de amortizare, componenta dupa axa d a tem E' devine, E'd= 0 si se sare la A13;
A12: daca G.S. considerat are infasurari de amortizare se calculeaza:

(4.80)
A13: expresia complexa, corespunzatoare planului d - q propriu G.S. rezulta:
![]()
(4.81)
A14: se trece la nodul urmator.
Algoritmul descris determina complet, pe baza relatiilor (4.72) - (4.81) modelul matematic al G.S. pe canalul electromagnetic, in regim dinamic al SEE.
4.1.3. Ecuatiile G.S. pe canalul electromecanic, in regim dinamic
In regimul dinamic al SEE datorita variatiilor lente ale marimilor termo si hidromecanice, marimile electromagnetice pot fi considerate cvasiconstante si ca urmare, curentii turbionari care se manifesta numai in statorul G.S. (confectionat din tole izolate intre ele) sunt foarte mici, efectul lor fiind neglijabil intr-o prima aproximatie. Ecuatia de miscare a rotorului, in acest caz, va fi influentata numai de prezenta infasurarilor de amortizare (daca ele exista) adica vom avea:

(4.82)
(4.83)
in care Pm - puterea mecanica la arborele turbinei se obtine rezolvand sistemul de ecuatii corespunzator instalatiilor primare.
Daca nu exista infasurari de amortizare, constanta de amortizare D1 = 0 si ecuatia (4.82) se simplifica mult.
Rezolvand la fiecare pas de calcul ecuatiile (4.82) si (4.83) se obtine pozitia rotorului G.S. fata de axa de referinta a unghiurilor tensiunilor din SEE, data de valoarea unghiului de stabilitate.
Cu aceasta se pot determina componentele t.e.m. tranzitorii, E' dupa axele generale X si Y ale planului complex al retelei electrice, adica:

(4.84)
Rezulta valoarea si faza t.e.m. tranzitorii, E' in planul complex al retelei:

(4.85)
(4.86)
Cu aceste valori constante pentru un pas de calcul se determina valorile si fazele tensiunilor din toate nodurile retelei si se face calculul circulatiei de puteri in SEE, la pasul respectiv conform metodei descrise in capitolul III.
Setul de ecuatii (4.77) - (4.86) descriu modelul matematic al G.S. in regimuri dinamice ale SEE. La acesta se vor adauga ecuatiile SRAE si RAT.
|
Politica de confidentialitate |
| Copyright ©
2026 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |