
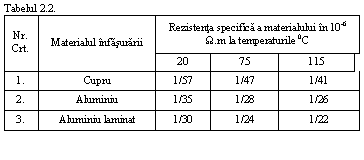
PARAMETRII PRINCIPALI, PIERDERILE SI RANDAMENTUL MASINILOR ELECTRICE
A. Parametrii masinilor electrice
Parametrii principali ai masinii electrice reprezinta coeficientii variabilelor independente din ecuatiile ce descriu conversia electromecanica a energiei. De obicei variabilele independente sunt curentii statorici si rotorici si atunci parametrii masinii electrice vor fi rezistentele active si reactive, respectiv momentul axial de inertie (prevazut in ecuatia fundamentala de miscare). In locul rezistentelor reactive (reactantele) adesea este mai comoda utilizarea inductantelor, astfel incat parametrii masinii sunt: inductivitatea totala L, mutuala M, de dispersie Lσ, rezistenta ohmica r si momentul axial de inertie J. In mod obisnuit primii patru parametrii se refera la o faza a masinii.
 A1. Rezistenta activa a unei
faze se determina cu relatia
A1. Rezistenta activa a unei
faze se determina cu relatia
![]() , (138)
, (138)
in care ![]() -
este rezistenta specifica a materialului din care este realizata
infasurarea; ea depinde de temperatura si unele valori ale
sale se dau in tabelul 2; l este
lungimea conductorului unei faze; S este
sectiunea, iar kr este coeficientul (supraunitar) care
tine seama de cresterea rezistentei active in urma
distributiei neuniforme a curentului in sectiunea conductorului.
Aceasta distributie neuniforma a curentului in sectiunea
conductorului se
-
este rezistenta specifica a materialului din care este realizata
infasurarea; ea depinde de temperatura si unele valori ale
sale se dau in tabelul 2; l este
lungimea conductorului unei faze; S este
sectiunea, iar kr este coeficientul (supraunitar) care
tine seama de cresterea rezistentei active in urma
distributiei neuniforme a curentului in sectiunea conductorului.
Aceasta distributie neuniforma a curentului in sectiunea
conductorului se
produce mai ales in cazul in care conductorul infasurarii
este format din mai multe "fire" si se dispune pe fundul unei
crestaturi sau spre istmul de deschidere a acesteia astfel incat
rezistenta reactiva a firelor conductorului nu este aceeasi.
Pentru amicsora ![]() se utilizeaza mai ales metoda transpozitiei
firelor conductorului astfel incat toate firele paralele sa fie supuse
acelorasi conditii.
se utilizeaza mai ales metoda transpozitiei
firelor conductorului astfel incat toate firele paralele sa fie supuse
acelorasi conditii.
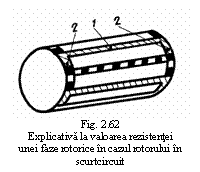
 La infasurarile realizate in scurtcircuit (in cazul
masinilor asincrone cu rotorul in scurtcircuit) - figura 62 - se
considera ca numarul fazelor infasurarii
(rotorice) m2, este egal cu
numarul barelor coliviei de veverita z2-adica
La infasurarile realizate in scurtcircuit (in cazul
masinilor asincrone cu rotorul in scurtcircuit) - figura 62 - se
considera ca numarul fazelor infasurarii
(rotorice) m2, este egal cu
numarul barelor coliviei de veverita z2-adica
m2 = z (139)
Deci rezistenta unei faze va fi egala cu rezistenta unei bare 1 si doua portiuni 2 din inelul de scurtcircuitare.
Determinarea inductivitatilor, respectiv a rezistentelor reactive pentru masinile electrice reprezinta una dintre problemele cele mai grele si in acelasi timp importante ale teoriei acestor masini.
A La determinarea inductivitatilor trebuie avut in vedere ca inductivitatile necesare sunt cele corespunzatoare unei faze a infasurarii in timp ce fluxul magnetic cu care se opereaza este fluxul de lucru al intregii masini, produs de curentii tuturor fazelor.
Daca amplitudinea curentului
printr-o faza a infasurarii este ![]() atunci
amplitudinea f.m.m. pe faza pentru armonica fundamentala- dupa (81)
este:
atunci
amplitudinea f.m.m. pe faza pentru armonica fundamentala- dupa (81)
este:
![]()
iar inductia magnetica din intrefier produsa de aceasta f.m.m. va fi:
![]() (141)
(141)
Daca se considera ca axa campului se suprapune peste axa infasurarii, atunci fluxul magnetic care se inlantuie cu infasurarea fazei este ,de exemplu, pentru faza A
![]() (142)
(142)
in careΦ1m este fluxul magnetic corespunzator armonicii fundamentale care se poate stabili cu (52) adica:
![]()
si pentru ca
![]()
atunci: ![]()
Inductivitatea fazei se determina apoi prin relatia sa de definitie:
![]() (143)
(143)
Pentru o infasurare m-fazata (cazul particular m=3), inductivitatea mutuala dintre infasurarile statorice sau rotorice este
![]()
iar pentru cazul m=3 rezulta:
![]() , (144)
, (144)
In ceea ce priveste campul de dispersie al unei infasurari - asa cum s-a prezentat deja - acesta are trei componente:
 - campul de dispersie de
crestatura;
- campul de dispersie de
crestatura;
- campul de dispersie frontal care se produce la capetele frontale ale infasurarii;
- campul de dispersie datorat armonicelor superioare sau campul diferential.
In general inductivitatea de dispersie a unei infasurari se determina cu relatia:
![]() (145)
(145)
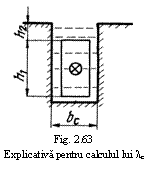
in care λσ=λc+λf+λd corespunde coeficientilor (adimensionali) de permeanta magnetica de crestatura, a partii frontale a infasurarii si dispersiei diferentiale a unei infasurari statorice sau rotorice. Pentru o crestatura deschisa de tip dreptunghiular - figura 63 - coeficientul λc se poate determina cu relatia:
λc=h1/3bc+h2/bc (146)
Liniile campului de dispersie se distorsioneaza daca se modifica profilul crestaturii si aceasta distorsiune este foarte puternica cand crestatura poseda o deschidere sub forma de istm. Efectul istmului se aproximeaza cu ajutorul unei componente specifice coroanelor dentare. Dispersia de crestatura este cu atat mai mare cu cat latimea crestaturii este mai mica, iar inaltimea mai mare.
Coeficientul λf se calculeaza cu o relatie semiempirica destul de complicata.
Coeficientul λd se poate calcula cu relatia:
![]() (147)
(147)
in care tz este pasul dentar, iar ξ=0,4.1 este un coeficient ce depinde de gradul de deschidere a crestaturii, de influienta curentilor turbionari si de felul executiei infasurarii. La masinile asincrone coeficientii λc, λf si λd au acelasi ordin de marime, iar la masinile sincrone mari λd este de obicei mai mic decat λc. Inductivitatea proprie L11 sumata cu cea de dispersie Lσ este egala cu inductivitatea totala L, care daca poarta indicele 1 se refera la infasurarea statorica (primara), respectiv indicele 2 pentru infasurarea rotorica (secundara). Cunoscand inductivitatile L, L12=M si Lσ, se obtin imediat rezistentele reactive (reactantele) respective: x=ωL, x12=ωM si xσ=ωLσ. De obicei reactantele xσ reprezinta de la cateva procente pana la 10.15% din x12, dar la micromasini ele pot fi mult mai mari.
Reactanta x12 depinde intr-o mult mai mare masura decat xσ, de efectul saturatiei magnetice, avand in vedere ca liniile campului de dispersie se inchid prin aer si nu poate fi vorba de saturatia magnetica a aerului, dar in cazul producerii unor scurtcircuite cand curentul creste de 10.15 ori peste cel nominal se produce si o modificare pronuntata a lui xσ.
A3. Pentru determinarea lui J avem: J=Jr+Jext unde momentul axial al rotorului este :
![]() , (148)
, (148)
in care ![]() este raza elementului de volum dv pana la
axa de rotatie, iar
este raza elementului de volum dv pana la
axa de rotatie, iar ![]() este densitatea materialului rotorului. Din (148) se vede ca Jr
depinde de raza
este densitatea materialului rotorului. Din (148) se vede ca Jr
depinde de raza ![]() si de aceea motoarele care lucreaza
tot timpul in procese tranzitorii se executa cu diametrul mic si de
lungime mai mare, iar in cazul motoarelor care lucreaza la o sarcina
pulsatorie - si deci au nevoie de Jr mai mare pentru nivelarea
vitezelor - acestea se vor executa cu diametre mari si de lungimi mici.
si de aceea motoarele care lucreaza
tot timpul in procese tranzitorii se executa cu diametrul mic si de
lungime mai mare, iar in cazul motoarelor care lucreaza la o sarcina
pulsatorie - si deci au nevoie de Jr mai mare pentru nivelarea
vitezelor - acestea se vor executa cu diametre mari si de lungimi mici. ![]() este momentul de inertie
corespunzator maselor "exterioare " masinii electrice.
este momentul de inertie
corespunzator maselor "exterioare " masinii electrice.
A4. Exactitatea solutiilor pentru conversia electromecanica a energiei depinde nu numai de corectitudinea ecuatiilor luate in consideratie ci si de exactitatea determinarilor parametrilor masinii, de aceea acestei probleme trebuie sa i se acorde suficienta atentie. In acest context trebuie amintit faptul ca la rezolvarea sistemelor de ecuatii legate de conversia electromecanica a energiei se utilizeaza asa - numitele unitati relative in care tensiunile, curentii, puterile si ceilalti parametri se exprima raportate la unele marimi de baza, care reprezinta valorile nominale ale unor parametri. Astfel marimile relative pentru curent, tensiuni si putere sunt:
I*=I/In; U*=U/Un
P*=P/Pn=mUI/(mUnIn)=U*I*. (149)
Pentru viteza si cuplu avem:
Ω*=Ω/Ωn=2пn/2пnn=n/nn;
M*=M/Mn=MΩn/Pn. (150)
Impedanta de baza se defineste prin:
Zb=Zn=Un/In, (151)
iar marimile relative pentru rezistente sunt:
r*=r/zn; x*=x/zn; z*=z/zn, (152)
respectiv pentru o inductivitate avem:
L*=L/Ln=ω1L/Zn. (153)
Toate ecuatiile masinilor electrice pot fi rescrise in unitati relative si aici apare avantajul ca pentru un timp dat de masina: parametrii masinii in unitati relative caracterizeaza insasi geometria masinii: dimensiunile sale, intrefierul sau si saturatia sa magnetica.
In cazul modelarii masinilor pe sisteme automate de calcul este necesar si un timp de baza care se defineste prin relatia :
Tb=1/ωb , (154)
in care ωb=2пf0=ω0.
B. Pierderile si randamentul masinilor electrice
In ceea ce priveste pierderile din masinile electrice trebuie avut in vedere faptul ca la conversia electromecanica a energiei: mecanica in cea electromecanica sau invers, o parte din energia electromecanica, respectiv cea mecanica se transforma in caldura. Aceasta parte din energie care se transforma in masinile si transformatoarele electrice in caldura este denumita, in mod obisnuit pierderi.
Pierderile la masinile electrice se pot imparti in doua categorii mari: pierderi de baza si pierderi suplimentare. La randul sau pierderile de baza sunt de trei tipuri: electrice, magnetice si mecanice.
B1 Pierderi electrice denumite si pierderi in cupru - includ pierderile prin efect Joule din infasurarile masinii si in contacte de perii (daca exista in masina astfel de contacte). Pierderile in infasurari se stabilesc cu relatia cunoscuta:
Pinf=mI²r0 (155)
in care I este curentul de baza, iar r0 este rezistenta activa a fazei la temperatura de calcul (pentru o masina de c.c avem m=1).
Pierderile in contactul de perii se determina in mod obisnuit cu relatia :
Pp=mΔUpI, (156)
in care ΔUp este caderea de tensiune pe rezistenta de contact dintre perie si inelul colector sau colector, si care depinde de tipul periei: pentru perii din carbune sau grafit ΔUp =1V, iar pentru perii din grafit metalizat ΔUp=0,3V.
B Pierderile magnetice includ pierderile in toate componentele circuitului magnetic al masinii in care campul magnetic variaza cu anumita frecventa. Aceste pierderi depinde de calitatea tablei electrotehnice sau a otelului utilizat, grosimea tolelor, valoarea inductiei si frecventa remagnetizarii. Asupra acestor pierderi au influente si unii factori tehnologici cum sunt: stantarea tolelor, presarea pachetul de tole, prelucrarea mecanica a circuitului magnetic.
Pierderile magnetice se refera la pierderile prin curenti turbionari (Foucault) si prin histerezis, iar determinarea lor aproximativa se poate face cu expresia:
![]() , (157)
, (157)
in care kp este coeficientul de prelucrare (supraunitar) care depinde de tehnologia prelucrarii tolelor (pentru motoare asincrone kp=1,41,8); psp sunt pierderile specifice - adica pierderile la frecventa de remagnetizare de 50 Hz cu inductia de 1T, in [W/kg]; β este exponentul ce depinde de calitatea otelului utilizat (β= 1,3.1.5); f este frecventa de remagnetizare, in [Hz]; B este inductia in portiunea corespunzatoare a circuitului magnetic pentru care se calculeaza pierderile, in [T]; G este greutatea portiunii de circuit respective, in [kg].
In privinta frecventei de remagnetizare f se mentioneaza ca ea poate fi de tip pulsatoriu ca in cazul transformatoarelor electrice (la care remagnetizarea miezului de fier se face cu ajutorul tensiuni alternative), respectiv de tip rotativ ca in cazul masinilor rotative. Ori in cazul inductiilor relativ mici pierderile prin histerezis in cazul frecventei de remagnetizare de tip rotativ pot fi mai mici (uneori chiar de 2 ori mai mici) decat in cazul frecventei de remagnetizare pulsatorii. Dar la inductii de 1,5..1,7 T pierderile in fier pentru ambele tipuri de frecvente de remagnetizare au aproximativ aceeasi valoare.
B3. Pierderile mecanice se refera la frecarea rotorului in aer, la frecarile in lagare, la frecarile periilor pe inele colectoare sau colector (daca este cazul) si la pierderile datorita ventilatiei (in cazul masinilor autoventilate la care rotorul ventilatorului este montat pe arborele masinii). La proiectarea masinii fiecare componenta se calculeaza separat, dar in principiu se poate spune ca pierderile mecanice depind de patratul turatiei masinii.
Pierderile prin frecarea rotorului in aer depind de densitatea aerului sau a mediului respectiv - de exemplu in cazul hidrogenului aceste pierderi sunt de 10 ori mai mici.
Pierderile prin frecare in lagare si pentru ventilatie (in cazul ventilatiei radiale) se pot calcula cu formula:
![]() (158)
(158)
in care k=5 pentru 2p=2 si k=6 pentru 2p≥4, iar Dr este diametru rotorului, in [m].
Pierderile prin frecarea periilor se pot calcula cu relatia :
Pfp=kfpφpSpVic (159)
in care kfp este
coeficientul de frecare al periilor (se ia kfp=0,1.0,2);φp
este presiunea realizata pe suprafata de contact a periilor, in [Pa
]; Sp este suprafata de contact a periei, in [![]() ]; Vic
este viteza periferica a inelelor colectoare in [m/s].
]; Vic
este viteza periferica a inelelor colectoare in [m/s].
B4. Pierderile suplimentare la randul lor se impart in pierderi suplimentare la mers in gol si pierderi suplimentare in sarcina.
Pierderile suplimentare la mers in gol se refera la pierderile superficiale si de pulsatie.
- Pierderile suplimentare superficiale se produc in stratul superficial al dintilor sau al polilor datorita campului pulsatoriu din intrefierul masinii. Frecventa pulsatiilor inductiei din intrefier se determina in functie de turatia masinii n si numarul dintilor z:
fz=nz/60 (160)
in care z este numarul dintilor statorici daca se calculeaza pierderile superficiale din rotor, respectiv numarul dintilor din rotor daca se determina pierderile din stator (n in t/min).
- Pierderile suplimentare de pulsatie sunt pierderile in fier care se produc datorita pulsatiei campului magnetic in dintii statorici si rotorici. Aceste pierderi depind de inductia din dinti si frecventa pulsatiilor care la randul sau pentru dintii statorici depinde de numarul dintilor rotorici si invers.
- Pierderile suplimentare la sarcina apar in infasurari si circuitul magnetic al masinii datorita fluxurilor de dispersie si deformarea campului magnetic din intrefier datorita sarcinii.
Calculul detaliat al pierderilor suplimentare se face pentru masini mari, iar pentru masini cu puteri curente pierderile suplimentare se iau (0,5.1)% din puterea motorului.
B5. Randamentul masinilor electrice
Avand precizate toate tipurile de pierderi se poate determina randamentul masinii:
- pentru generatoare avem:
ηG=[1-∑p/(P2+∑p)]100, (161)
- pentru motoare avem:
ηM=(1-∑p/P1)100, (162)
 in care P1 este puterea absorbita; P2 este
puterea utila, iar ∑p este suma pierderilor din masina. In
figura 64 este dat graficul η =f(P2) in unitati
relative. Forma graficului η=f(P2) pentru o tensiune U=const se
explica prin aceea ca la cresterea sarcinii puterea utila
creste proportional cu curentul de sarcina, iar pierderile
electrice cresc cu patratul aceluiasi curent. Randamentul are
valoarea maxima cand pierderile constante sunt egale cu pierderile
variabile-pierderile constante fiind cele ce nu depind de sarcina.
Pierderile constante cuprind in general pierderile magnetice si mecanice
in cazul in care turatia masinii nu depinde (sau depinde intr-o
mica masura) de sarcina. Pierderile variabile se
refera la cele electrice pentru ca ele depind de patratul curentului
de sarcina.
in care P1 este puterea absorbita; P2 este
puterea utila, iar ∑p este suma pierderilor din masina. In
figura 64 este dat graficul η =f(P2) in unitati
relative. Forma graficului η=f(P2) pentru o tensiune U=const se
explica prin aceea ca la cresterea sarcinii puterea utila
creste proportional cu curentul de sarcina, iar pierderile
electrice cresc cu patratul aceluiasi curent. Randamentul are
valoarea maxima cand pierderile constante sunt egale cu pierderile
variabile-pierderile constante fiind cele ce nu depind de sarcina.
Pierderile constante cuprind in general pierderile magnetice si mecanice
in cazul in care turatia masinii nu depinde (sau depinde intr-o
mica masura) de sarcina. Pierderile variabile se
refera la cele electrice pentru ca ele depind de patratul curentului
de sarcina.
Avand in vedere ca in practica exploatarii masinilor electrice se constata ca acestea sunt subincarcate cu 15.25%, din proiectarea acestora se cauta ca randamentul lor sa atinga valoare maxima la circa 0,6.0,8 din sarcina nominala.
La masini electrice mari (800.1000MW) randamentul poate atinge valori mari η=0,988, dar la micromasini el poate fi de numai η=0,1.0, La transformatoare de puteri foarte mari avem η=0,997, ceea ce nu se poate obtine la alte tipuri de convertoare de energie.
15. Elemente de sinteza a masinilor electrice
La masinile electrice de tip inductiv, cea mai mare parte a energiei campului magnetic se concentreaza in intrefierul acestora si in zona dintilor statorici/rotorici, de aceea alegerea volumului intrefierului masinilor si calcului zonei dintilor are cea mai mare importanta in sinteza - adica in proiectarea -acestor masini.
Densitatea specifica a energiei din intrefierul unei masini poate fi reprezentata prin raportul dintre puterea activa a masinii P si volumul intrefierului Vδ - adica
![]() (215)
(215)
in care
![]() (216)
(216)
unde s-a notat: lδ - lungimea intrefierului (pachetul de tole statorice /rotorice ); δ=R-r; iar ρ=(R+r)/2 este raza medie.
Parametrul ps se modifica destul de putin pentru o serie de masini cu variatia foarte mare a puterilor - astfel, de exemplu, pentru seria 4A a motoarelor asincrone avem urmatoarele date [3]:
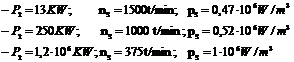
De aceea este normal ca proiectarea (sinteza) masinilor electrice sa inceapa cu alegerea lui ps; dupa care se determina Vδ, respectiv se dimensioneaza circuitul magnetic si infasurarile masinii.
Pe de alta parte, se poate lua in considerare asa-numita constanta a masinilor electrice definita prin relatiile
![]() (217)
(217)
in care D este diametrul rotoric la
masini de c.c. sau diametrul interior al statorului la masini de
c.a., in [m]; n este turatia masinii, in [t/min]; p este puterea de
calcul ,in [w]; ![]() - unde
αp este coeficientul polar; kw este coeficientul de
infasurare , iar kf este coeficientul de forma al
campului magnetic; Bδ este inductia magnetica din
intrefier; A=2mwI/πD este sarcina liniara a masinii, in [A/m] (m
- numarul de faze ; w - numarul de spire pentru o faza ).
- unde
αp este coeficientul polar; kw este coeficientul de
infasurare , iar kf este coeficientul de forma al
campului magnetic; Bδ este inductia magnetica din
intrefier; A=2mwI/πD este sarcina liniara a masinii, in [A/m] (m
- numarul de faze ; w - numarul de spire pentru o faza ).
In mod obisnuit parametrii CME, Bδ si A sunt date - pentru diverse puteri si turatii de sincronism - in tabele de proiectare. Astfel, Bδ se alege astfel incat in dintii statorici / rotorici inductia sa nu depaseasca 1,4.1,8T, iar sarcina (incarcarea) liniara sa nu fie mai mare de 40000 A/m. Este stiut ca cresterea parametrilor Bδ si A duce la micsorarea gabaritului masinii, respectiv la scaderea pretului sau de cost, dar odata cu aceasta cresc pierderile din masina, respectiv scade randamentul acesteia. De aceea, exista rapoarte optime intre Bδ, A si dimensiunile de gabarit ale masinii.
In alta ordine de idei, este stiut ca partea cea mai solicitata termic este infasurarea masinii, iar temperatura unor parti constructive ale masinii depinde de sistemele de racire, de regimurile de functionare ale masinii, dar si de suprafata de racire a acesteia. De aceea la proiectarea unei serii de masini electrice se tinde spre o similitudine geometrica a acestora. In acest caz raportul dintre lungimea activa a masinii Iδ si diametrul statoric / rotoric, ramane constant pentru diverse puteri de masini.
In general insa puterea unei masini este proportionala cu o lungime de baza a masinii la puterea a patra: si aceasta rezulta din urmatoarele considerente:
avem lδ~l, deci si D~l;
sectiunea circuitului magnetic este deci i~12;
sectiunea cuprului infasurarilor este, de asemenea ~l
Costul unei masini insa (se admite) este proportional cu masa sa, adica ~13 , iar pierderile sunt si ele proportionale cu masa materialelor active, respectiv ~l3. De aici rezulta ca este mai convenabil sa se execute o singura masina de putere mare decat mai multe masini de puteri mai mici cu aceeasi suma a puterilor, avand in vedere ca in primul caz pierderile specifice sunt mai mici, iar necesarul specific de materiale active este si el mai mic.
Evolutia constructiilor de masini electrice arata ca parametrii energetici ai acestora se modifica pozitiv, in timp ce masa lor scade. In ultimii ani s-au obtinut rezultate deosebite in proiectarea masinilor electrice prin utilizarea sistemelor automate de calcul si prin automatizarea proiectarii masinilor electrice (complex de masini automate de calcul si pachet de programe cu ajutorul caruia se realizeaza toate lucrarile de calcul, proiectare-constructie).
16. Exemple si probleme pentru capitolul 2
Problema 1. Sa se construiasca schema desfasurata pentru o infasurare trifazata tetrapolara (2p=4), in doua etaje cu o singura cale de curent si avand q = 2 crestaturi pe pol si faza.
Rezolvare. Numarul total de crestaturi in care se amplaseaza infasurarea este
![]()
iar pasul principal y1 daca se ia diametral (y1 = τ) atunci
![]()
Infasurarea este reprezentata in figura 69 a. Daca inceputul fazei (A-X) se gaseste in crestatura 1, atunci inceputul fazei urmatoare (B-Y) se va gasi decalat cu pasul
yf = 2q + 6kq
in raport cu crestatura 1, ceea ce pentru k = 0 inseamna
![]()
respectiv va fi amplasat in crestatura 1+4 = 5, iar pentru k = l avem
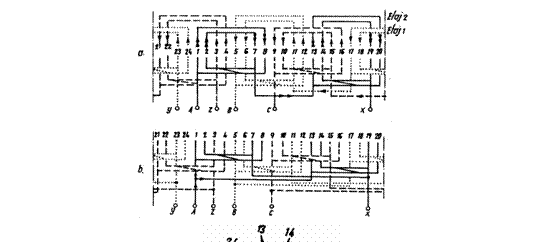
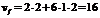
respectiv inceputul va fi amplasat in crestatura 1+16 = 17.
In schema din figura 69 a inceputul fazei (B-Y) este amplasat in crestatura 5, iar inceputul fazei (C-Z) in crestatura 5+4=9. De fapt inceputurile fazelor trebuie sa fie decalate spatial intre ele cu un unghi electric αel=1200. La 24 de crestaturi, intre doua crestaturi avem un unghi geometric αel =360/24 = 150, respectiv trebuie sa avem egalitatea
![]()
din care rezulta
![]()
care corespunde cu yf pentru cazul k=0.
Din schema desfasurata a infasurarii rezulta ca aceasta este simetrica in raport cu fazele - fiecare faza este compusa din bobine care se inchid la etajul l si la etajul Daca insa prin dispunerea capetelor de bobina in cele doua etaje se asigura aceeasi parametri electrici a grupelor de bobina de etaj, atunci acestea (adica grupele de bobina de etaj) se pot lega si in paralel, formand o infasurare cu p cai de curent. Aceasta situatie este reprezentata in figura 69 b.
In ceea ce priveste steaua tensiunilor - reprezentata in figura 69 c - unghiul dintre doua raze este
![]()
iar steaua va avea
![]()
raze distincte. Factorul de infasurare este kw = kr pentru ca ks si ki sunt unitare (pas diametral si crestaturile nu sunt inclinate).
Problema Sa se prezinte schema desfasurata pentru o infasurare trifazata, in doua straturi, cu p = l si q = 3.
Rezolvare. Numarul crestaturilor infasurarii este
![]()
iar numarul bobinelor pe o faza se deduce dupa relatia
![]()
Admitand un pas diametral pentru infasurare avem
![]()
Din problema 1 s-a vazut ca grupele de bobina de strat se pot conecta in serie (pentru cazul infasurarii cu o cale de curent) sau in paralel (pentru cazul infasurarii cu doua cai de curent).
La o infasurare bipolara (p=1) cu o cale de curent, cele doua grupe de bobine (de strat) care se succed in crestaturile armaturii si apartin aceleiasi faze sunt situate intre ele la o 'distanta' de un pas polar τ si se conecteaza intre ele in opozitie, pentru a se obtine insumarea solenatiilor dintr-o crestatura (adica curentul sa circule in acelasi sens prin laturile bobinelor din cele doua straturi ale aceleiasi crestaturi) cand aceasta se gaseste sub un anumit pol magnetic. Bobinele unei astfel de infasurari cu mai multe spire au forma unor bucle - de unde denumirea de infasurare buclata.
 Reprezentarea
acestei infasurari este data in figura 70 unde este
data si steaua crestaturilor, respectiv diagrama fazoriala.
Reprezentarea
acestei infasurari este data in figura 70 unde este
data si steaua crestaturilor, respectiv diagrama fazoriala.
Astfel, faza (A-X) cuprinde grupele de bobine (1-10), (2-11) si (3-12) conectate in opozitie cu grupa bobinelor (12-3), (11-2) si (10-l), iar in diagrama fazoriala t.e.m. induse in aceste bobine au fost notate cu semnul minus(-).
Daca se considera o infasurare multipolara cu p perechi de poli, atunci schema sa desfasurata se poate obtine prin repetarea de p ori a schemei anterioare.
In cazul in care infasurarea are o singura spira per bobina atunci aceasta se realizeaza, in general, din bare conductoare si ea se denumeste infasurare in bare; ea se mai numeste si infasurare ondulata deoarece pentru a evita legaturile frontale dintre bobinele (realizate din bare) aceleiasi faze, aceste bobine se executa (la sablon) sub forma unor ondule.
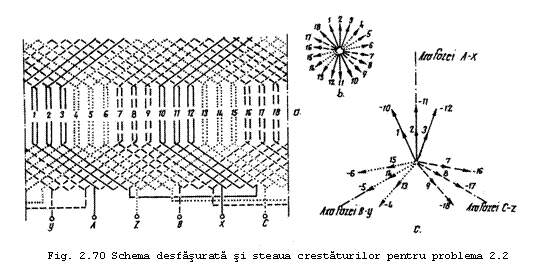
Problema 3. Sa se realizeze schema desfasurata pentru o infasurare trifazata in doua straturi eu un numar fractionar de crestaturi pe pol si faza, avand p=2 si q=5/4.
Rezolvare Numarul total al crestaturilor este Z=2mpq=2·3·2·5/4=15, iar numarul de bobine pe faza va fi nbf=Z/m=15/3=5.
Pe de alta parte, infasurarea se va putea executa numai daca numarul de raze distincte din steaua crestaturilor este divizibil cu numarul de faze m. Dar numarul de raze distincte din steaua crestaturilor este dat de raportul Z/t - unde t este cel mai mare divizor comun al numarului de crestaturi Z si al numarului de perechi de poli p - adica rezulta conditia:
![]() = numar intreg (218)
= numar intreg (218)
In cazul dat este evident ca t=1 (cel mai mare divizor comun pentru Z=15 si p=2) si atunci numarul razelor distincte pentru steaua crestaturilor este Z/t=15/1=15, iar conditia (218) este indeplinita.
Pasul principal al infasurarii este:
![]()
adica este fractionar si deci infasurarea se poate executa numai cu pas scurtat, y1=3 crestaturi sau pas lungit cu y1=4 crestaturi.
Se admite (din motive cunoscute) o infasurare eu pas scurtat y1=3 crestaturi, atunci pasul inceputurilor de faza
![]() (219)
(219)
ne da pentru cazul k=0-yf = 2·5/4 = 2·1/2 (ceea ce nu este posibil pentru ca yf trebuie sa fie un numar intreg), iar pentru cazul k=1 avem yf=10.
Se mai pune probleme repartizarii celor 5 bobine corespunzatoare unei faze pe cei 4 poli (pentru ca p=2): aceasta se poate face montand doua bobine sub un pol si cate o bobina sub fiecare din ceilalti trei poli. Schema desfasurata si steaua crestaturilor este data in figura 71.
 Observatie.In legatura eu exemplele de
infasurari prezentate se poate mentiona ca au fost
luate in considerare numai infasurari trifazate simetrice, cu
bobine (sectii) identice (adica cu acelasi numar de spire)
si care se dispun in mod uniform in crestaturile armaturilor
magnetice.
Observatie.In legatura eu exemplele de
infasurari prezentate se poate mentiona ca au fost
luate in considerare numai infasurari trifazate simetrice, cu
bobine (sectii) identice (adica cu acelasi numar de spire)
si care se dispun in mod uniform in crestaturile armaturilor
magnetice.
Exista insa infasurari monofazate, care se executa la fel ca si cele trifazate dar se repartizeaza numai pe 2/3 din totalul crestaturilor armaturii (motoare asincrone monofazate)
Exista, de asemenea, asa numitele infasurari bifazate, care sunt formate din doua infasurari monofazate decalate intre ele eu un unghi electric de 90°.
Se mai executa si infasurari sinusoidale formate din sectii (bobine avand un numar diferit de spire prin care se urmareste obtinerea unei unde de tensiune magnetica cat mai apropiata de o sinusoida - in acest caz numarul de spire din crestaturi variaza avand o distributie sinusoidala (aproximativ !) pe distanta unui dublu pas polar (2τ).
Probleme 4. Se admite ca un motor functioneaza la sarcina nominala, iar temperatura aerului de racire este de 35°C ceea ce conduce la o supratemperatura a motorului de θn=6o°C (deci temperatura sa interna este τ=95°C).
Daca apare o suprasarcina cu multiplul k1=5 si o durata t=l0s se pune probleme cum se modifica uzura relative a izolatiei infasurarilor sale.
Rezolvare: Expresia din (214) pentru uzura relativa se poate nota in acest caz sub forma:
![]() (220)
(220)
in care T reprezinta constanta de timp la incalzire si ea poate fi determinata cu relatia [6]
![]() (221)
(221)
in care kR este un factor ce tine seama de cresterea rezistentei conductorilor electrici datorita efectului de refulare a curentului cand acesta este alternativ iar J este valoarea nominala a densitatii curentului electric.
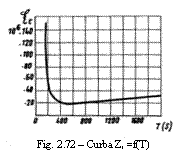
In general pentru statorul motoarelor asincrone se poate lua kR=l, iar pentru rotoarele lor, de asemenea, kR=1 daca turatia lor nu scade mai mult de 20%; la o scadere mare a turatiei rotorului este posibil sa se ajunga chiar la kR=3. In figura 72 este data variatia Zr=ξc=f(T) pentru k1=5 si t1=10s. Din aceasta curba rezulta ca uzura minima a izolatiei se produce pentru infasurari cu T=700s, iar pentru infasurari cu T<300s, uzura creste foarte mult.
Astfel, daca se admite Jn=5A/mm2 si θn=60°C, atunci constanta de timp la incalzire a infasurarii statorice este:
![]()
deci destul de apropiata de cea optima.
Se presupunem insa ca motorul are T=175s si este supus la o suprasarcina cu k1=5 si t1=l0s o singura data pe zi. Valoarea relativa a uzurii suplimentare datorita suprasarcinii pe o zi, obtinuta eu relatia (220) este Zr=165·l06, iar pe un an:
![]()
Valoarea relativa a uzurii izolatiei pentru restul anului este determinata de temperatura de lucru a infasurarii, in regim nominal (adica τ=95sC). Din relatia (204) rezulta:
![]()
in oare intervalul Δt se obtine scazand din numarul total al secundelor unei zile (24·60·60=86400s) durata suprasarcinii t1=l0s si durata racirii ~ 3T=3·175=525s si apoi tinand seama de perioada unui an.
Deci rezulta:
![]()
Durata de serviciu a motorului este:
![]()
Uzura izolatiei intr-un an daca nu ar exista suprasarcini este:
![]()
iar durata de serviciu in conditiile inexistentei suprasarcinilor ar fi:
![]()
![]()
Comparand datele de serviciu in cele doua cazuri, rezulta ca producerea suprasarcinilor reduce durata de serviciu cu 28,5%. Este important de remarcat ca efectul suprasarcinilor asupra duratei de serviciu scade cu cat creste T. Astfel, pentru T=800s in conditiile mentionate anterior reducerea duratei de serviciu este de numai 3%.
|
Politica de confidentialitate |
| Copyright ©
2026 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |