
Punti de curent alternativ
Puntile de curent alternativ, rezulta uneori din schema puntii Wheatstone, prin inlocuirea rezistentelor din laturi cu impedante, alimentarea de la o sursa de tensiune alternativa si folosirea unui detector (indicator) de nul de curent alternativ.
Alteori,
schemele difera destul de mult de puntea Wheatstone, continand numai
doua impedante, celelalte doua laturi fiind formate din
sectiunile unor infasurari ale unor transformatoare sau
divizoare de tensiune inductive acestea fiind denumite punti cu
transformatoare. In practica se intalnesc insa si tipuri
speciale de punti de curent alternativ. Puntile de curent alternativ realizeaza
masurarea parametrilor de circuit, (R, L, C, M sau Z, ![]() ori R, X) putandu-se
clasifica in punti pentru masurarea capacitatilor, a
inductivitatilor, a impedantelor etc. De o larga utilizare
sunt puntile universale, care pot masura toti parametrii
elementelor de circuit dipolare (R, L, C).
ori R, X) putandu-se
clasifica in punti pentru masurarea capacitatilor, a
inductivitatilor, a impedantelor etc. De o larga utilizare
sunt puntile universale, care pot masura toti parametrii
elementelor de circuit dipolare (R, L, C).
Puntea simpla de curent alternativ
Schema generala a puntii simple in curent alternativ (forma la care ce reduc multe dintre schemele mai complicate) este cea din figura 3.71.
Conditia de echilibru a puntii de curent alternativ este:
![]() (3.224)
(3.224)
Aceasta
conditie este analoaga cu cea din cazul puntii Wheatstone in
curent continuu, in care ![]() sunt impedante
din laturile puntii scrise ca marimi complexe. Conditia de
echilibru exprimata prin expresia (3.224) in marimi complexe conduce
la doua relatii in marimi reale, obtinute prin scrierea
impedantelor prin una din formele obisnuite:
sunt impedante
din laturile puntii scrise ca marimi complexe. Conditia de
echilibru exprimata prin expresia (3.224) in marimi complexe conduce
la doua relatii in marimi reale, obtinute prin scrierea
impedantelor prin una din formele obisnuite:
![]() (3.225)
(3.225)
unde R si X
reprezinta rezistenta si reactanta impedantei
reprezentata printr-o schema serie, iar Z si ![]() modulul, respectiv argumentul impedantei.
Folosind prima exprimare se obtin relatiile:
modulul, respectiv argumentul impedantei.
Folosind prima exprimare se obtin relatiile:
![]() (3.226)
(3.226)
iar daca se utilizeaza scrierea exponentiala rezulta:
![]() (3.227)
(3.227)
relatii echivalente cu (3.226).
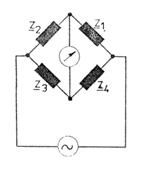
Fig.3.71 Puntea simpla in c.c.
Principalele particularitati ale puntii de curent alternativ sunt urmatoarele:
Conditia de echilibru este data de un sistem de doua ecuatii, deci puntea permite determinarea a doua necunoscute alese a fi rezistenta si reactanta impedantei necunoscute Zx. Indeplinirea conditiei de echilibru se poate realiza prin reglarea a doua (sau mai multe) din celelalte sase marimi ce intervin in ecuatiile (3.2.2.6) toate trebuind sa fie cunoscute.
Prin adoptarea pentru Z1, Z2, Z3, Z4 a unor combinatii de rezistente, capacitati si inductivitati in serie sau in paralel, se pot obtine o multime de tipuri de punti.
Conditia de faza ![]() arata ca nu
orice combinatie de impedante poate conduce la o punte
echilibrata; semnul reactantelor din brate trebuie sa fie
astfel, incat conditia de faza sa poata fi satisfacuta.
Aceasta limiteaza numarul posibil de tipuri de punti.
arata ca nu
orice combinatie de impedante poate conduce la o punte
echilibrata; semnul reactantelor din brate trebuie sa fie
astfel, incat conditia de faza sa poata fi satisfacuta.
Aceasta limiteaza numarul posibil de tipuri de punti.
O
alta conditie limitativa este data de cerinta ca cele doua
marimi masurate de punte sa poata fi citite separat
(independent) pe indicatoarele celor doi parametri variabili ai puntii. Se
poate arata ca acest lucru este posibil daca doua din
impedantele puntii sunt fie rezistente pure, fie reactante
pure (adica doua din unghiurile ![]() sa fie 0,
sa fie 0, ![]() sau
sau ![]() ).
).
In general impedanta de masurat este complexa, de forma:
![]() (3.228)
(3.228)
Aceasta implica existenta in punte a cel putin unui brat complex. Celelalte doua brate se aleg practic totdeauna de forma Z=R sau Z=jX.
Bratul
complex, de impedanta ![]() , se numeste brat
de referinta (sau brat de comparatie) al puntii.
, se numeste brat
de referinta (sau brat de comparatie) al puntii.
Bratele simple, de forma Z=R sau Z= jX, se numesc brate auxiliare ale puntii. Bratele auxiliare pot fi alaturate sau opuse in schema puntii (bratul necunoscut si bratul de referinta vor fi de asemenea, alaturate, respectiv, opuse in aceste cazuri).
Puntile in care bratele auxiliare sunt opuse, se numesc punti de produs.
Puntile in care bratele auxiliare sunt alaturate se numesc punti de raport.
Aceste denumiri provin de la faptul ca pentru o punte de raport la care Z3 este brat de referinta:
![]() (3.229)
(3.229)
si
bratele auxiliare intra in ecuatia de echilibru ca un raport ![]() . La aceste punti masurarea poate fi privita
ca o comparare a impedantei Zx cu impedanta Z3.
Factorul
. La aceste punti masurarea poate fi privita
ca o comparare a impedantei Zx cu impedanta Z3.
Factorul ![]() poate fi real sau
imaginar. Daca
poate fi real sau
imaginar. Daca ![]() este real, puntea
compara doua impedante de acelasi fel (ambele inductive sau
ambele capacitive).
este real, puntea
compara doua impedante de acelasi fel (ambele inductive sau
ambele capacitive).
Pentru o punte de produs la care Z2 este brat de referinta:
![]() (3.230)
(3.230)
si
bratele auxiliare intra in conditia de echilibru ca un produs Z1Z3.
La aceste punti masurarea poate fi privita ca o comparare a impedantei
Zx cu admitanta ![]() . Factorul Z1Z3 poate fi real sau imaginar.
Daca Z1Z3 este real, puntea compara doua
impedante de feluri diferite (una inductiva cu una capacitiva).
. Factorul Z1Z3 poate fi real sau imaginar.
Daca Z1Z3 este real, puntea compara doua
impedante de feluri diferite (una inductiva cu una capacitiva).
Puntile
care masoara componentele vectorului ![]() adica valorile
elementelor serie Rx si Xx, se numesc punti serie. Asemenea punti
sunt fie punti de raport cu bratul de referinta format din
elemente serie, pentru care:
adica valorile
elementelor serie Rx si Xx, se numesc punti serie. Asemenea punti
sunt fie punti de raport cu bratul de referinta format din
elemente serie, pentru care:
![]() ,
,
fie punti de produs cu bratul de referinta format din elemente paralel, pentru care:
![]()
Puntile care masoara direct componentele vectorului Yx adica valorile elementelor paralel Gx si Bx se numesc punti paralel. Asemenea punti sunt fie punti de raport cu bratul de referinta, format din elemente paralel, pentru care:
![]() ,
,
fie punti de produs cu bratul de referinta format din elemente serie, pentru care:
![]() .
.
Dupa pozitia elementelor variabile ale puntii, care servesc pentru echilibrare, exista doua posibilitati principale:
a) sunt variabile cele doua componente ale bratului de referinta. In acest caz, puntea masoara perechi de componente ca R si X, R si L, G si B sau G si C.
b) sunt variabile una din componentele bratului de referinta si un brat auxiliar. In acest caz puntea masoara o componenta a impedantei Zx si factorul de calitate Q (sau D=1/Q).
In general, o punte de curent alternativ nu poate fi echilibrata cu elemente variabile plasate numai in bratele auxiliare.
Echilibrarea se poate face si cu unul sau ambele elamente variabile plasate in bratul necunoscut (in serie sau in paralel cu impedanta de masurat). In acest caz, are loc o masurare prin substitutie, intrucat se compenseaza efectul introducerii impedantei Zx in punte prin scaderea sau cresterea corespunzatoare a impedantei din acelasi brat.
Pentru o sistematizare a principalelor tipuri de punti de curent alternativ pot fi luate in considerare urmatoarele criterii:
natura impedantei masurate: capacitiva sau inductiva (punti RC, respectiv punti RL);
schema echivalenta a bratului necunoscut: punti serie, punti paralel;
schema echivalenta a bratului de referinta: serie, paralel;
pozitia bratelor auxiliare: punti de raport, punti de produs.
Pentru simplificare pot fi considerate numai acele punti ale caror elemente componente sunt rezistoare si condensatoare, ceea ce corespunde practicii actuale (bobinele nu se folosesc in puntile moderne).
Pentru bratele auxiliare prezinta interes numai perechile rezistor-rezistor si rezistor-condensator (brate auxiliare condensator-condensator sunt folosite rar). Pozitia sursei si a indicatorului de nul nu este necesar sa fie precizate. In aceste conditii sunt posibile 16 scheme distincte de punti reprezentate in figura 3.72.
Sensibilitatea puntilor de curent alternativ
Ca si in cazul puntilor de curent continuu, problema sensibilitatii puntilor de curent alternativ este destul de complicata, daca trebuie sa se tina seama de toti parametrii care intervin.

Fig.3.72 Punti de c.a. clasificate dupa structura bratelor
In cazul in care impedanta indicatorului de nul este suficient de mare pentru a considera ca puntea lucreaza in gol, o expresie generala a tensiunii de dezechilibru a puntii este:
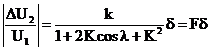 (3.231)
(3.231)
unde F este
factorul de raport al puntii, K este modulul si ![]() argumentul raportului
bratelor puntii adiacente indicatorului de nul,iar
argumentul raportului
bratelor puntii adiacente indicatorului de nul,iar ![]() este abaterea
relativa a impedantei unuia din bratele puntii.
este abaterea
relativa a impedantei unuia din bratele puntii.
Daca impedanta indicatorului de nul este finita, atunci o conditie de sensibilitate maxima este ca impedanta indicatorului de nul sa fie conjugata complexa a impedantei de iesire a puntii:
 (3.232)
(3.232)
Practic aceasta conditie este indeplinita foarte rar. Daca este necesara obtinerea unei sensibilitati apropiate de cea maxima, se asigura egalitatea modulelor celor doua impedante prin alegerea adecvata a indicatorului de nul sau cu ajutorul unui transformator de adaptare.
Procesul de echilibrare a puntii de curent alternativ
Pentru echilibrarea unei punti de curent-alternativ, doua din elementele sale (doua rezistente, o rezistenta si o reactanta sau doua reactante) trebuie sa fie variabile. Se pun urmatoarele conditii:
a) alegerea elementelor variabile sa fie astfel incat echilibrarea sa fie totdeauna posibila;
b) echilibrarea sa fie cat mai rapida, adica cu putine reglaje succesive ale celor doua elemente.
Tensiunea
de dezechilibru a puntii, in ipoteza ![]() este
este
![]() (3.233)
(3.233)
Oricare ar fi elementele variabile, in cursul echilibrarii puntii prin varierea unuia din aceste elemente, vectorul U2 descrie un cerc in planul complex. Echilibrarea prin reglaje succesive ale celor doua elemente variabile face ca vectorul U2 sa descrie segmente de cerc (fig.3.73 a). Daca aceste segmente sunt din ce in ce mai mici, procesul conduce efectiv la echilibrarea puntii: se spune ca puntea este convergenta.
Usurinta
echilibrarii depinde de numarul de reglaje succesive necesare; se
poate arata ca acesta, deci rapiditatea convergentei, este
determinat de unghiul sub care se intersecteaza cele doua cercuri
corespunzatoare reglarii celor doua elemente variabile ale puntii.
Convergenta optima se obtine pentru valoarea ![]() a unghiului-.de
convergenta
a unghiului-.de
convergenta ![]() . In general, numarul de reglaje succesive necesare
pentru a micsora de m ori tensiunea de dezechilibru este:
. In general, numarul de reglaje succesive necesare
pentru a micsora de m ori tensiunea de dezechilibru este:
 (3.234)
(3.234)
unde ![]() este unghiul de
insensibilitate al indicatorului, datorita imposibilitatii
aprecierii exacte a minimului tensiunii de iesire (fig.3.73 b). De obicei
este unghiul de
insensibilitate al indicatorului, datorita imposibilitatii
aprecierii exacte a minimului tensiunii de iesire (fig.3.73 b). De obicei ![]() pentru indicatoarele
obisnuite. Daca
pentru indicatoarele
obisnuite. Daca ![]() echilibrarea nu mai
este posibila. Convergenta este satisfacatoare daca
echilibrarea nu mai
este posibila. Convergenta este satisfacatoare daca ![]()

Fig.3.73
Puntile
la care componentele Rx si Xx (sau Gx
si Bx) se echilibreaza independent (de exemplu puntea
Maxwell-Wien, avand ca elemente variabile R2 si C2)
au unghiul de convergenta ideal ![]() .
.
La
puntile care masoara Xx si Qx (sau Xx
si Dx) unghiul de convergenta este ![]() ; aceste punti au o convergeta slaba la
masurarea impedantelor cu unghi de faza mic (de exemplu bobine
cu pierderi mari).
; aceste punti au o convergeta slaba la
masurarea impedantelor cu unghi de faza mic (de exemplu bobine
cu pierderi mari).
|
Politica de confidentialitate |
| Copyright ©
2025 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |