
Rezonanta la conectare serie-paralel
Se considera circuitul din figura 8, obtinut prin conectarea in paralela doua circuite serie R, L si R, C. Daca impedantele complexe ale celor doua ramuri sunt :
Z = R1 + jwL (37)
Z = R2 + ![]() (38)
(38)
impedanta echivalenta a circuitului va fi :
Ze =
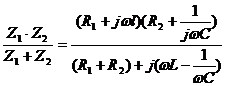 (39)
(39)
Dupa transformari simple se obtine forma :
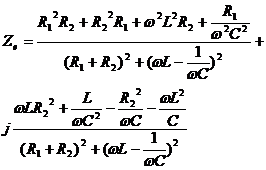 (40)
(40)
In circuitul considerat va exista rezonanta cand reactanta echivalenta (coeficientul lui j din relatia 40) se anuleaza, adica :
![]() (41)
(41)
Rezolvand aceasta ecuatie, se obtine pulsatia de rezonanta :
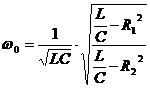 (42)
(42)
Aceasta expresie arata ca in circuitul considerat, pulsatia de rezonanta depinde si de rezistentele R1 si R2 din circuit, spre deosebire de rezonanta din circuitele ideale (par. 1 si 2), unde pulsatia de rezonanta era functie numai de parametri L si C .
Observatii :
a) Cand rezistentele R1
si R2 sunt egale (sau cand sunt nule) pulsatia de
rezonanta este egala cu pulsatia de rezonanta ideala ![]()
b) Pentru ![]() si
si ![]() (sau invers),
rezulta o pulsatie de rezonanta imaginara, deci circuitul nu va
fi rezonat pentru nici o pulsatie.
(sau invers),
rezulta o pulsatie de rezonanta imaginara, deci circuitul nu va
fi rezonat pentru nici o pulsatie.
c) In cazul particular ![]() , rezulta o nedeterminare a pulsatiei de
rezonanta, deci circuitul este rezonant pentru orice pulsatie. Acest
circuit se numeste complet aperiodic si este utilizat in masuri electrice.
, rezulta o nedeterminare a pulsatiei de
rezonanta, deci circuitul este rezonant pentru orice pulsatie. Acest
circuit se numeste complet aperiodic si este utilizat in masuri electrice.
|
Politica de confidentialitate |
| Copyright ©
2026 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |