
1 PREDICTIA LINIARA
1.1 IDENTIFICAREA PARAMETRICA LINIARA
Pentru realizarea studiului oricarui sistem, este necesara modelarea acestuia. Modelarea este reprezentarea unui sistem printr-un alt sistem, denumit model, mai usor de studiat si care pastreaza caracteristicile importante ale originalului. Scopul ei il reprezinta obtinerea unor concluzii relevante ale originalului, pe baza studierii modelului. In cazul sistemelor din domeniul autovehiculelor, modelele sunt matematice si descriu functionarea acestora in conditiile existentei unor perturbatii impuse sau apreciate de cel ce realizeaza studiul [22; 36; 66].
Stabilirea modelului matematic pe baza datelor experimentale constituie singura posibilitate de a valida valorile adoptate teoretic. Tot cu ajutorul experimentarilor se poate stabili daca forma modelului este cea adecvata[36; 66].
Metodele parametrice utilizeaza descrieri matematice analitice in domeniul timpului, din rezolvarea carora rezulta comportarea dinamica a sistemului vizat, respectiv se obtin caracteristici dinamice.
Metodele de identificare neparametrice sunt in domeniul timpului, in cel al frecventei sau in timp-frecventa si folosesc: analiza proceselor tranzitorii (in domeniul timpului); analiza de coreatie (in domeniul timpului); analiza spectrala (in frecventa si in timp-frecventa), in ultimul caz rezultand caracteristici de frecventa si caracteristici in timp-frecventa (sau caracteristici de realocare).
1.2 PREDICTIA LINIARA SIMPLA
Predictia este o simulare prin care se incearca reproducerea unui proces de un anumit numar de ori, in conditii identice de desfasurare. Pentru calcule sunt necesare:
seriile de date ale marimilor de intrare si iesire rezultate din determinari experimentale;
modelul matematic al procesului, in cazul de fata fiind vorba de un model liniar obtinut prin identificarea sistemelor;
orizontul de predictie; el stabileste de cate ori se reproduce procesul.
Rezultatul predictiei sunt serii de date calculate cu o anumita precizie (intr-un anumit interval de incredere, in cazul de fata 95%), stabilita anterior [3].
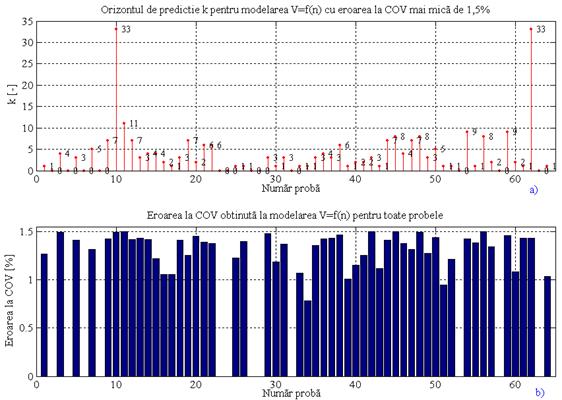
Graficele ce apar in fig.8 s-au obtinut prin predictionarea cu orizont variabil
si cu eroarea la COV impusa la valoarea de 1,5% pentru toate probele.
Modelul ales este de tip SISO (single input single autput o intrare o
iesire) in care marimea de intrare este turatia motorului, iar
cea de iesire este viteza autovehiculului. In fig.8a sunt reprezentate
orizonturile de predictie rezultate din conditia impusa la
eroare, pentru toate cele 64 de probe. In fig.8b apar erorile la COV ce s au obtinut prin predictionarea cu valorile maxime ale lui k rezultate din
conditia de mai sus, pentru fiecare proba in parte. Se constata
ca pentru anumite probe eroarea obtinuta este mai mare decat
limita impusa inca de la prima predictie, k 1, si ca atare, in grafic k 0. Pentru alte probe insa, k ia diferite valori.
Se observa ca erorile obtinute la predictie variaza de la proba la proba, pentru aceeasi valoare a lui k si acelasi tip de model ales, aspect normal avand in vedere ca pentru fiecare proba au fost alte conditii de desfasurare si deci alte functii de transfer.

In fig.14
este vorba despre predictii de tipul ![]() si proba I5n.
Ipoteza nula
si proba I5n.
Ipoteza nula ![]() este respectata
atat timp cat k<55, dar eroarea la COV rezultata pentru predictia cu orizontul k=54 depaseste pragul de 4% fig.14a. Criteriul principal avut in vedere in analiza
modelarii il constituie valoarea erorii serie obtinute, rezultatele
analizei dispersionale intervenind ulterior.
este respectata
atat timp cat k<55, dar eroarea la COV rezultata pentru predictia cu orizontul k=54 depaseste pragul de 4% fig.14a. Criteriul principal avut in vedere in analiza
modelarii il constituie valoarea erorii serie obtinute, rezultatele
analizei dispersionale intervenind ulterior.
Valorile coeficientilor
predictiilor ![]() ,
,![]() pentru toate cele 64 de probe experimentale sunt prezentate
in fig.15. Pentru fiecare proba si tip de predictie rezulta
cate un rand de coeficienti, astfel incat in figuri apar seturi de 64 de
valori. Majoritatea valorilor coeficientilor se regaseste in
zone concentrate din intreaga plaja de variatie (zonele
ingrosate din grafice), ceea ce sugereaza
utilizarea valorilor medii.
pentru toate cele 64 de probe experimentale sunt prezentate
in fig.15. Pentru fiecare proba si tip de predictie rezulta
cate un rand de coeficienti, astfel incat in figuri apar seturi de 64 de
valori. Majoritatea valorilor coeficientilor se regaseste in
zone concentrate din intreaga plaja de variatie (zonele
ingrosate din grafice), ceea ce sugereaza
utilizarea valorilor medii.
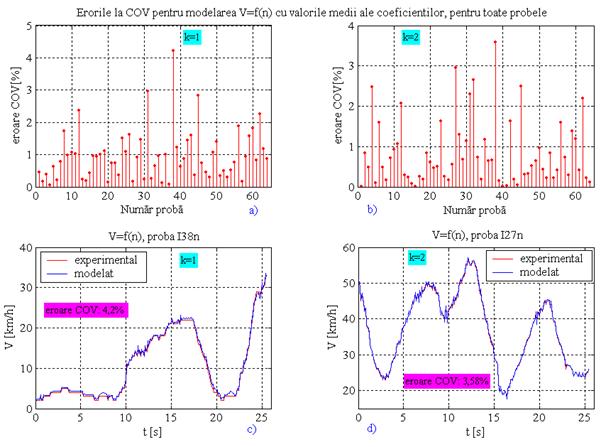
In fig.17 este exemplificata folosirea valorilor medii ale coeficientilor corespunzatoare tuturor celor 64 de probe, la predictii ale vitezei autovehiculului functie de turatia motorului. Este vorba de valorile erorilor obtinute prin predictionarea cu k=1 (fig.17a) si k=2 (fig.17b), pentru toate probele. Erorile maxime rezultate corespund probelor I38n in primul caz si I27n, in cel de al doilea, si sunt egale cu 4,2% si 3,58%. Din grafice rezulta ca se pot utiliza cu succes coeficientii medii, erorile, cu singura exceptie, avand valori sub 4%. In fig.17c si fig.17d apar seriile dinamice ale vitezelor obtinute pe cale experimentala si modelare pentru probele I38n si I27n.
 |
1.3 PREDICTIA LINIARA MULTIPLA
Se constata aceeasi tendinta remarcata si in cazul regresiilor analizate in capitolul precedent, ca atat valorile maxime cat si cele medii ale erorilor scad odata cu cresterea numarului de intrari, confirmand ideea ca un volum de informatie mai mare duce la cresterea preciziei de modelare.
Tabelul 1
|
Tipul modelarii- Numarul figurii |
Eroarea maxima |
Eroarea medie |
Tipul modelarii Numarul figurii |
Eroarea maxima |
Eroarea medie |
|
|
3,41% |
0,90% |
|
1,64% |
0,53% |
|
|
3,25% |
1,03% |
|
0,84% |
0,21% |
|
|
2,60% |
0,66% |
|
0,82% |
0,19% |
|
|
1,39% |
0,34% |
|
0,57% |
0,16% |
|
|
1,38% |
0,32% |
|
0,51% |
0,12% |
|
|
1,12% |
0,20% |
|
0,46% |
0,10% |
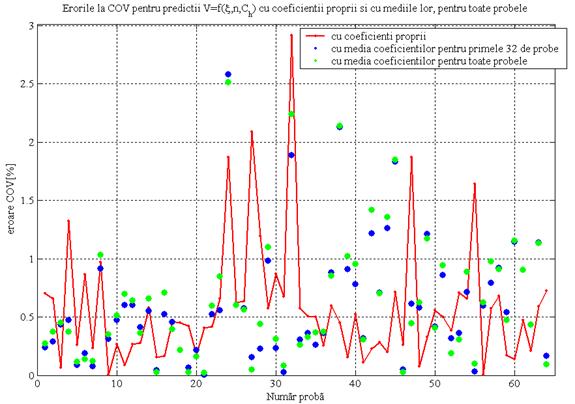
Daca se compara erorile obtinute la predictionarea ce foloseste valori medii ale coeficientilor cu erorile rezultate la predictionarea cu coeficientii proprii se obtin grafice precum cele din fig.41 si fig.42. In exemplele date marimile de intrare sunt in numar de trei, iar cele de iesire sunt momentul motor (fig.41) si viteza autoturismului (fig.42). Spre deosebire de predictia liniara simpla, unde erorile obtinute la modelarea cu coeficienti proprii sunt, in general, mai mari decat cele de la modelarea cu coeficienti medii, in predictia liniara multipla situatia este inversa. Diferentele nu sunt semnificative, dar sunt mai mari in cazul in care marimea de rezultativa este momentul motor decat in cazul in care aceasta este viteza autovehiculului, datorita influentei factorului "drum" ce nu este contorizata decat indirect, prin pozitia clapetei obturatoare. Probele s-au desfasurat in conditii diferite, seriile dinamice rezultate pastrand aceasta informatie. Cu cat ea este mai bogata, cu atat va suplini mai bine lipsa celei legate de drum.
Erorile obtinute la modelarea cu coeficienti medii la care s au folosit doar primele 32 de probe sunt mai mici decat cele la rezultate la utilizarea intregului pachet de probe. Acest fapt demonstreaza ca majoritatea valorilor coeficientilor se afla in apropierea mediilor coeficientilor primelor 32 de probe. Diferentele sunt mai mari in cazul momentului motor decat in cazul vitezei, motivul fiind cel prezentat mai inainte.
 |
Predictia liniara multipla aduce un plus de precizie fata de predictia liniara simpla, in modelarea dinamicii autovehiculului. Utilizarea valorilor medii ale coeficientilor obtinuti prin utilizarea tuturor probelor conduce la stabilirea ecuatiilor ce constituie modelul dinamic al tipului de autovehicul analizat.
2 PREDICTIA NELINIARA
Una din cele mai folosite metode de predictie neliniara apeleaza la retele neuronale. Folosirea retelelor neuronale la procesele neliniare se justifica prin faptul ca ambele au capacitatea de "autoorganizare (autoinstruire)"; din acest motiv se si spune ca retelele neuronale sunt cele ce definesc cel mai bine sistemele "inteligente", ceea ce de altfel justifica si denumirea de "neuronal", cu trimitere la neuronul biologic.
Principial, algoritmii care utilizeaza retele neuronale pentru stabilirea modelelor matematice (pentru identificarea sistemelor) in vederea predictiei sunt aceiasi ca cei proprii metodelor parametrice liniare; spre exemplu, corespondentul algoritmului ARMAX este NNARMAX (Neural Network AutoRegressive Moving Average with eXogenous Inputs) [1; 5; 6; 15; 41]

In fig.55 se prezinta reteaua neuronala ce permite stabilirea dependentei dintre viteza automobilului si momentul motor. Daca se liniarizeaza parametrii retelei neuronale, atunci se obtin variatiile coeficientilor din fig.56; dupa cum se constata, descrierile matematice cu retele neuronale sunt cu coeficienti variabili, cee ce confirma caracterul nestationar al sistemelor reale.
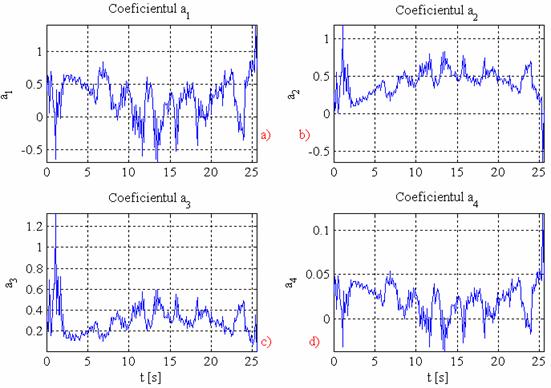
Fig.56
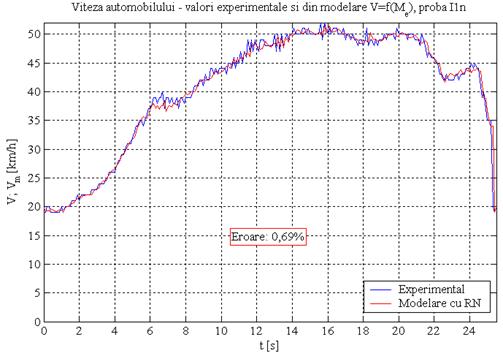
Fig.57
In fig.57 se prezinta rezultatul utilizarii retelei neuronale, eroarea de modelare obtinuta, de 0,69%, fiind o valoare acceptabila.
Se poate concluziona ca stabilirea unor modele matematice neliniare folosind retele neuronale poate asigura precizia dorita, care se obtine comod prin marirea numarului de neuroni din legile ascunse.
|
Politica de confidentialitate |
| |
Copyright ©
2026 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |