Coeficientul simplu de corelatie liniara

Coeficientul simplu de corelatie liniara

Coeficientul simplu de corelatie liniara - ca forma particulara a raportului de corelatie - se aplica numai in cazul corelatiei sintetizata prin ecuatia de regresie,  y = a + bx

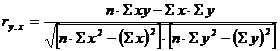
in care: n = numarul variantelor

Marimea acestui coeficient se poate situa intre -1 si +1, semnul coeficientului aratand sensul legaturii (inversa, cand are semnul minus sau directa cand este pozitiv). Cu cat coeficientul simplu de corelatie are o valoare mai apropiata de +1 sau de -1, cu atat legatura dintre fenomenele sistemului studiat este mai puternica si, dimpotriva, cu cat valoarea sa se apropie de 0 se apreciaza ca interdependenta este mai slaba sau inexistenta. Interpretarea acestui coeficient pe intervale de marimi, indiferent de semnul rezultatului, este similara cu aceea prezentata in cazul raportului de corelatie.

Daca este supus studiului un sistem multiplu de corelatie este posibil sa se calculeze un raport de corelatie multiplu dar si coeficienti de corelatie partiala. In Anexa 7 este prezentata metodologia statistica de calcul a coeficientilor de corelatie partiala.

se verifica semnificatia indicatorului care exprima intensitatea corelatiei cu ajutorul "Criteriului F". Folosirea acestui criteriu de testare a semnificatiei raportului de corelatie se aplica prin compararea variabilei F-statistic cu variabila F-tabelar care corespunde probabilitatii P = 0,95 si numarului gradelor de libertate, f₁ = k - 1 si f₂ = n - k ,

Daca F-statistic > F-tabelar, ipoteza nula" este respinsa si deci, raportul de corelatie este semnificativ diferit de zero.

In acelasi timp, raportul de corelatie si expresia relativa a estimatiei erorii standard a ecuatiei de regresie () confirma prin marimea lor ca, ecuatia de regresie formalizeaza corect, din punct de vedere analitic, legitatea statistica a corelatiei dintre variabilele sistemului considerat si poate fi utilizata cu suficienta incredere pentru a estima niveluri viitoare ale variabilei dependente in conditiile adoptarii unor variante posibile ale marimii variabilelor independente.

* se calculeaza coeficientul de determinare in forma procentuala, astfel:

In cazul corelatiilor simple se calculeaza coeficientul simplu de determinare, pe baza relatiei:

sau, ;

iar in cazul corelatiilor multiple, se calculeaza coeficientul multiplu de determinare:

Coeficientul de determinare exprima cat la suta din modificarea (variatia) indicatorului rezultativ (y) este determinata de modificarea (variatia) indicatorului (indicatorilor) factorial sau independent din sistemul interdependent considerat. Diferenta pana la 100% este reprezentata de influenta altor factori care nu au fost cooptati in sistemul studiat.

* se calculeaza estimatia erorii medii a ecuatiei de regresie (estimatia erorii standard a regresiei) in expresie absoluta:

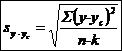, si in expresie relativa:

Acest indicator exprima puterea" ecuatiei de regresie, atunci cand este folosita in calcule de extrapolare sau de prognoza. Se considera o eroare medie relativa de o marime foarte buna, cand aceasta se situeaza sub 5% si de o marime buna, cand are o valoare cuprinsa intre 5% si 10% . Interpretarea acestui indicator de eroare este complementara concluziei oferita de criteriul statistic DURBIN-WATSON

O semnificatie statistica similara aceleia pe care o ofera eroarea medie relativa a ecuatiei de regresie este obtinuta prin calculul si interpretarea "Coeficientului de neregularitate al lui Theil" care se determina astfel:

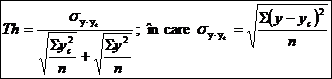
Coeficientul de neregularitate al lui Theil poate lua o valoare cuprinsa intre zero si unu. Daca, , valorile estimate ale variabilei dependente () exprima perfect prognoza fenomenului. Se considera ca fiind o marime foarte buna a coeficientului de neregularitate al lui Theil atunci cand nu depaseste limita de 5%.

Exemplul.9

Pentru a formula o concluzie corecta cu privire la existenta sau inexistenta unei corelatii (dependente) intre doua variabile se poate utiliza "Criteriul ca suport statistico-matematic de testare a ipotezei propuse. Exemplificarea modalitatii in care "Criteriul ofera informatia necesara cu privire la aceasta testare o vom realiza pe baza datelor referitoare la optiunea pentru a viziona filme politiste si sexul persoanelor intervievate.

Tabelul 9

Gruparea persoanelor dupa sex si optiunea pentru filme politiste

Distributia frecventelor teoretice este obtinuta prin aplicarea urmatoarei relatii de calcul:

Verificarea ipotezei propuse se realizeaza prin compararea lui - statistic cu - tabelar, astfel:

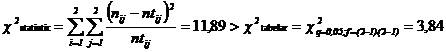
Deoarece se respinge ipoteza nula si deci exista suficient temei pentru a considera ca intre optiunea pentru filme politiste si sexul persoanelor intervievate este interdependenta. Concluzia formulata este garantata cu o probabilitate de 95%.

Nota: Valoarea tabelara a lui a fost extrasa din "Anexa 3" pentru o probabilitate de 95% si 1 grad de libertate (f = 1), , unde "v" reprezinta numarul randurilor si "c" numarul coloanelor.

Exemplul 10

Exemplificarea metodologiei statistice pentru analiza corelatiei dintre fenomene (metode statistico-matematice sau parametrice de analiza a corelatiei) va fi efectuata pe baza seriilor dinamice a doi indicatori statistici, prezentati intr-o forma conventionala, "dinamica cheltuielilor pentru servicii" (SERIA 01) - variabila dependenta (y) si "dinamica veniturilor" (SERIA 02) - variabila independenta (x).

Tabelul 10

Dinamica veniturilor si cheltuielilor pentru servicii

Reprezentarea grafica a corelatiei dintre seria 01 si seria 02 este expusa in figura 8.

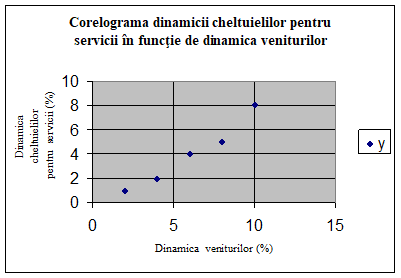
Fig. 8

Pe baza reprezentarii grafice din figura 8 se conchide ca ecuatia de regresie, y = a + bx, sintetizeaza in mod corespunzator interdependenta dintre cele doua variabile deoarece distributia norului de puncte se grupeaza in jurul unei linii drepte.

Sistemul de ecuatii necesar calculului valorilor estimate ale parametrilor ecuatiei de regresie, "a" si "b", se realizeaza cu ajutorul metodei celor mai mici patrate. In cazul exemplului considerat, sistemul de ecuatii care a rezultat prin aplicarea metodei celor mai mici patrate, este:

Pentru rezolvarea sistemului de ecuatii se poate opta pentru una din metodele cunoscute: substitutie, metoda lui Cramer (cu ajutorul determinantilor) sau matricial.

Exemplificam calculul matricial al parametrilor ecuatiei de regresie, deoarece, de regula, programele informatice aplica aceasta metodologie.

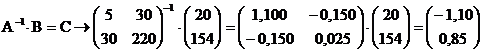
in care:

A reprezinta matricea sistemului de ecuatii

A^-1 este matricea inversa a matricei A

B reprezinta vectorul termenilor liberi

C reprezinta vectorul coeficientilor ecuatiei de regresie

(a = -1,10, b = 0,85).

Vectorul B poate fi obtinut si prin efectuarea produsului dintre transpusa matricei aferente variabilei independente si vectorul variabilei dependente (y), astfel:

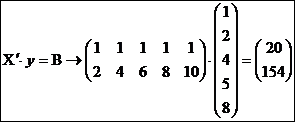
Calculul termenilor care formeaza vectorul coeficientilor ecuatiei de regresie, se realizeaza prin inmultirea matricei () cu vectorul (B), astfel:

Calculul matricei inverse a matricei A se desfasoara astfel:

transpusa asociatamatricea

matricei A = transpusei   inversa = A^-1

matricei A

Transpusa matricei A: - liniile devin coloane:

Asociata transpusei: - elementele transpusei matricei A se inlocuiesc cu complementii algebrici - ,

in care:

i este notatia generala acordata liniei

j este notatia generala acordata coloanei,

adica:

Minorii, , se calculeaza dupa ce se ignora linia si coloana elementului din matricea care urmeaza sa fie inlocuit. Minorii sunt reprezentati de valoarea unui determinant daca matricea are trei sau mai multe linii si coloane sau de o valoare simpla daca matricea este formata din doua linii si doua coloane.

Se remarca faptul ca semnele elementelor din matricea asociata transpusei () alterneaza.

Pentru a obtine matricea inversa, fiecare termen al asociatei transpusei matricei A se imparte la valoarea determinantului aferent matricei sistemului de ecuatii.

Valoarea determinantului aferent matricei sistemului de ecuatii este:

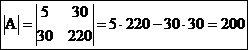
Rezulta ca ecuatia de regresie are urmatoarea forma:

Parametrul, b = 0,85, este denumit coeficient de regresie sau propensiunea marginala deoarece cuantifica modificarea fenomenului dependent atunci cand variabila independenta se modifica cu o unitate.

Calculul valorii estimate a erorii standard pentru fiecare parametru al ecuatiei de regresie are la baza urmatoarea metodologie:

a- se calculeaza produsul estimatiei patratului erorii standard a ecuatiei de regresie cu matricea inversa a matricei sistemului de ecuatii,

Acelasi rezultat se obtine daca se opteaza pentru urmatoarea varianta de lucru:

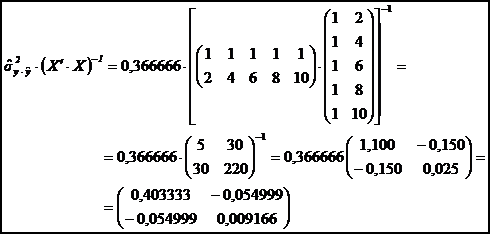
Se mentioneaza ca matricea inversa a sistemului de ecuatii este explicata prin urmatoarea relatie:

b- se calculeaza estimatia erorii standard a parametrului a,

c- se calculeaza estimatia erorii standard a parametrului b,

Se precizeaza ca estimatia erorii standard a parametrilor ecuatiei de regresie este reprezentata prin radacina patrata a elementelor situate pe diagonala principala a matricei (), in care patratul estimatiei erorii standard a ecuatiei de regresie (), se calculeaza, astfel:

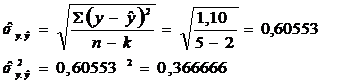
Verificarea semnificatiei parametrilor ecuatiei de regresie este realizata prin compararea variabilei t-statistic cu t-tabelar.

Daca, t-statistic > t-tabelar , se respinge ipoteza nula si in aceste conditii parametrii ecuatiei de regresie sunt semnificativ diferiti de zero.

Variabila t-statistic se obtine raportand estimatia parametrului la estimatia erorii standard asociata fiecaruia dintre parametrii ecuatiei, astfel:

- pentru parametrul a,

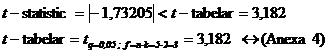
- pentru parametrul b,

In cazul studiului corelatiei dintre dinamica cheltuielilor pentru servicii - variabila dependenta (y) si dinamica veniturilor - variabila independenta (x) se confirma statatistic ca parametrul "b" are o marime semnificativa in timp ce parametrul "a" nu este atestat statistic ca o marime semnificativ diferita de zero. In principiu, aceasta concluzie nu afecteaza, insa, utilitatea ecuatiei de regresie deoarece infirmarea semnificatiei parametrului "a" (ordonata la origine) este si o consecinta a numarului redus de valori luate in calcul (n = 5).

Analiza sistemului interdependent de indicatori statistici prezentati sub forma celor doua serii dinamice se bazeaza pe interpretarea indicatorilor analitici prezentati in tabelul 11.

Tabelul 11

Sistemul indicatorilor analitici care privesc corelatia dintre SERIA 01 si SERIA 02

Metodologia de calcul a indicatorilor din tabelul 11 este urmatoarea:

- Coeficientul de determinare ()

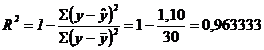
Intervalul de localizare a coeficientului de determinare si respectiv a raportului de corelatie este:

- Raportul de corelatie (R) se obtine prin extragerea radacinii patrate din coeficientul de determinare, , si indica, pentru corelatia studiata, o intensitate foarte puternica.

- Coeficientul de determinare corectat in functie de numarul gradelor de libertate aferente celor doua sume de patrate,

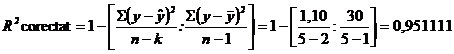
in care:

k - numarul parametrilor din ecuatia de regresie

n - numarul observatiilor

- Estimatia erorii standard a ecuatiei de regresie,

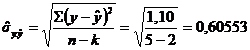
- Suma patratelor reziduurilor sau erorilor,

Se testeaza ipoteza privind existenta autocorelatiei intre valorile variabilei reziduale cu ajutorul criteriului statistic DURBIN-WATSON,

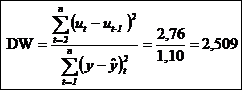, in care:

In acest caz indicatorul statistic DW are o marime care depaseste limita de 2,2 si obtinem astfel informatia ca la nivelul valorilor reziduale se inregistreaza o usoara autocorelatie, fapt ce poate afecta eficacitatea ecuatiei de regresie daca aceasta va fi folosita pentru extrapolarea dinamicii studiate. O explicatie a acestei concluzii poate fi argumentata prin faptul ca studiul corelatiei este realizat, pe seama unui volum prea mic de date.

- Valoarea medie a variabilei dependente,

- Estimatia abaterii standard a variabilei dependente,

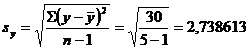
- Verificarea semnificatiei raportului de corelatie cu ajutorul Criteriului F",

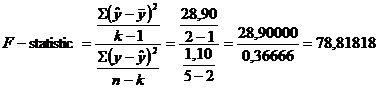
- estimatia dispersiei dintre sisteme

- estimatia dispersiei din interiorul sistemelor

- estimatia dispersiei totale

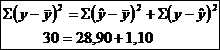
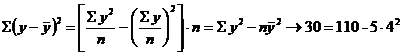
F -statistic = 78,81818 > F -tabelar = 10,1

F tabelar =

Deoarece, F-statistic > F-tabelar se respinge ipoteza nula si in consecinta Raportul de corelatie (R) difera in mod semnificativ de zero, iar corelatia studiata este reala. In Anexa 8 este prezentat un tabel cu ajutorul caruia se poate proceda la verificarea semnificatiei coeficientul simplu de corelatie liniara - ca forma particulara a raportului de corelatie.

Nota:- Se mentioneaza ca, F-statistic este un criteriu cu ajutorul caruia se testeaza veridicitatea modelului (ecuatiei de regresie) in ansamblul sau. Prin aceasta testare se verifica, de asemenea, ipoteza de valoare "zero" a tuturor coeficientilor de regresie, respectiv a coeficientilor variabilelor independente, cu exceptia coeficientului care dimensioneaza ordonata la origine. Valoarea critica a acestui indicator, (F-statistic), este 2,7 ce corespunde unei probabilitati de 95% si care atesta ca cel putin un coeficient de regresie este in mod semnificativ diferit de zero.

In cazul exemplului considerat de noi, probabilitatea de a accepta ipoteza nula este foarte mica: 0,003013 sau 0,30%. Riscul de a formula o concluzie gresita este, in aceasta situatie, practic inexistent.

- Regula de adunare a dispersiilor se verifica numai atunci cand nu se tine seama de numarul gradelor de libertate aferente fiecarei sume de abateri ridicate la patrat si deci fiecare din cele trei sume de abateri ridicate la patrat se raporteaza la numarul observatiilor (n).

Tabel pentru efectuarea calculelor intermediare

Anul	y	= -1,10 + 0,85x
1	1	= -1,10 + 0,85(2) = 0,6				0,4		0,16
2	2	= -1,10 + 0,85(4) = 2,3				-0,3		0,09
3	4	= -1,10 + 0,85(6) = 4,0				0		0
4	5	= -1.10 + 0,85(8) = 5,7				-0,7		0,49
5	8	= -1,10 + 0,85(10) = 7,4				0,6		0,36
Total	20	20,0				0		1,10
Anul	t = 2,.,n								y2	xy
1			-3,4	11,56	-3		9		1	2
2	0,49		-1,7	2,89	-2		4		4	8
3	0,09		0	0	0		0		16	24
4	0,49		1,7	2,89	1		1		25	40
5	1,69		3,4	11,56	4		16		64	80
Total	2,76		0	28,90	0		30		110	154	Nivelurile calculate ale variabilei dependente , determinate pe baza ecuatiei de regresie, pot fi obtinute si in varianta de calcul matricial, astfel: In tabelul 12 se prezinta, in mod comparativ, seria reala a variabilei dependente sau rezultative (y) cu nivelurile, aceleiasi variabile, estimate pe baza ecuatiei de regresie (), precum si distributia erorilor (reziduurilor). Tabelul 12 Situatia reziduurilor: marimile absolute si dispunerea grafica Anul Nivelurile reale (y) SER01 Nivelurile calculate sau estimate*) () SER01F Reziduuri (Termenul de eroare) u = y- Plaja reziduurilor 1 1,00000 0,60000 0,40000 * | 2 2,00000 2,30000 -0,30000 | 3 4,00000 4,00000 0,00000 | 4 5,00000 5,70000 -0,70000 | 5 8,00000 7,40000 0,60000 | + 0,60553 = + - 0,60553 = - *) Nivelurile calculate sau estimate ale variabilei dependente sunt determinate pe baza ecuatiei de regresie: y = a + bx  Este un indiciu pozitiv al eficientei modelului sintetizat prin ecuatia de regresie, atunci cand dimensiunea reziduurilor nu depaseste plaja delimitata de o estimatie a erorii standard a ecuatiei de regresie,(). - Experienta practica asigura suportul de apreciere a faptului ca se indelineste in mod implicit conditia de normalitate a distributiei seriei erorilor (reziduurilor) daca n > 40, atunci cand sunt date de natura experimentala sau, n > 15 in cazul seriilor dinamice. Estimarea parametrilor care localizeaza o ecuatie de regresie poate fi efectuata si cu ajutorul unor metode considerate mai putin eficiente, in comparatie cu metoda celor mai mici patrate, dar suficient de utile pentru a identifica forma ecuatiei de regresie. In aceasta categorie de metode sunt incluse: - metoda punctelor empirice alese si - metoda totalurilor partiale echidistante sau metoda mediilor echidistante. Politica de confidentialitate .com Copyright © 2024 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. Comentarii literare ALEXANDRU LAPUSNEANUL COMENTARIUL NUVELEI Amintiri din copilarie de Ion Creanga comentariu Baltagul - Mihail Sadoveanu - comentariu BASMUL POPULAR PRASLEA CEL VOINIC SI MERELE DE AUR - comentariu Personaje din literatura Baltagul – caracterizarea personajelor Caracterizare Alexandru Lapusneanul Caracterizarea lui Gavilescu Caracterizarea personajelor negative din basmul Tehnica si mecanica Cuplaje - definitii. notatii. exemple. repere istorice. Actionare macara Reprezentarea si cotarea filetelor Economie Criza financiara forteaza grupurile din industria siderurgica sa-si reduca productia si sa amane investitii Metode de evaluare bazate pe venituri (metode de evaluare financiare) Indicatori Macroeconomici Geografie Turismul pe terra Vulcanii Și mediul Padurile pe terra si industrializarea lemnului STATISTICA PRODUCTIEI INDUSTRIALE Bazele statisticii datelor experimentale Indicatori ai variatiei si ai imprǍstierii Indicatorii absoluti si indicatorii derivati Semnificatii ale termenului de statistica Coeficienti de corelatie. Coeficienti de corelatie Pearson si Spearman. Regresia. Predictia cu precizie. Raportul de corelatie DISTRIBUTIILE CLASICE - BAZA VERIFICARII IPOTEZELOR STATISTICE APLICABILE IN COMERT - TURISM - SERVICII Testul t. Compararea a doua esantioane de scopuri corelate/relationate. Termeni si conditii Contact Creeaza si tu