
APLICATII LA PRELUCRAREA SEMNALELOR
Introducere
Exemplele prezentate acest capitol se refera la trei aspecte importante din domeniul prelucrarii semnalelor numerice:
Sinteza sau elaborarea de semnale;
. Analiza frecventei si studiul imbunatatirii spectrului de frecventa prin utilizarea diferitelor temporale;
Studiul raspunsului la impuls a unui filtru numeric de ordinul doi.
In vederea dezvoltarii unor astfel de aplicatii, programul LabVIEW dispune, asa cum am vazut in capitolul anterior, de o serie de functii specifice care sunt abordabile prin Analysis din lista Functions. Aceste functii specifice sunt:
- generarea de semnale (Signal Generation) - Figura 2.1;
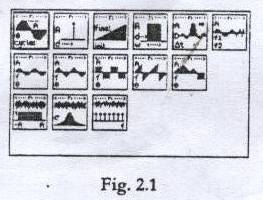
- prelucrarea semnalelor (Signal Processing) - Figura 2.2;
- filtrarea semnalelor (Filters) - Figura2.3;
- ferestre temporale (Windows) - Figura 2.4;
- functii statistice (Statistics) - Figura 1.47 (Capitolul I);
- regresii (Regression) - Figura 1.48 (Capitolul I );
- functi de algebra lincaia (Linear Algebra) - Figura 1.49 (Capitolul I);
- functii matriciale (Array & Numeric) - Figura 1.50 (Capitolul 1);
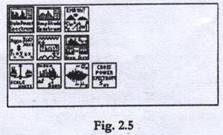
- masuratori (Measurement) - Figura 2.5.



1. Sinteza semnalelor
1.1. Scopul si bazele teoretice
Sinteza semnalelor si programele Lab VIEW urmareste:
. elaborarea de semnale plecandu-se de la descompunerea in serii Fourier a semnalelor periodice;
. studiul influentei numarului de armonici;
studiul semnalelor de diferite forme (dreptunghiulare si triunghiulare).
Teoria referitoare la sinteza semnalelor poate fi abordata incepand cu
prezentarea unor functii periodice s(t) cu perioada T0 =1 / F0 sub forma unei sume
de functii sinusoidale de frecventa f in care f este un multiplu al frecventei fundamentale F0.
![]()
unde an si bn sunt coeficientii Fourier care se determina cu relatiile:
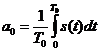
in care a0 reprezinta valoarea medie sau componenta continua. Pentru n≥ 1:
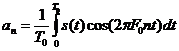

Seria Fourier se poate scrie sub forma:
![]()
cu ![]() si
si 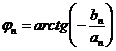
Cateva exemple de semnale periodice simple sunt prezentate in
continuare:
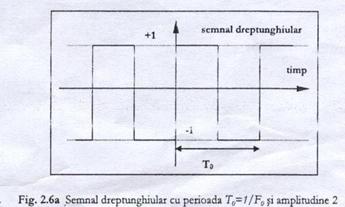
. semnalul dreptunghiular (Figura 2.6.a):
![]()
semnalul triunghiular (Figura 2.6.b):

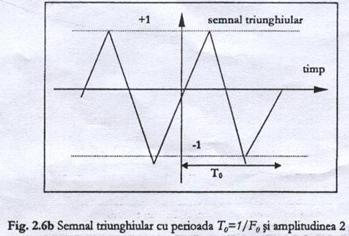
1.2. Realizarea unui instrument virtual
Definirea instrumentului virtual
Pentru realizarea unui instrument virtual trebuie:
1. sa se defineasca instrumentul (printr-o relatie matematica sau de alt tip);
2. sa se construiasca instrumentul cu ajutorul structurilor de calcul sau a simbolurilor grafice;
De exemplu, pentru sinteza unor semnale periodice plecand de la o functie sinusoidala se poate utiliza relatia:
![]()
in care k si c sunt parametrii.
Intrucat aceasta functie apare frecvent, se poate realiza un modul independent sau un instrument virtual care va putea fi copiat si reutilizat in alte aplicatii.
Pentru instrumentul virtual bazat pe relatia de mai sus se va preciza ca:
. parametrii de intrare sunt k, c si variabila x;
. parametrul de iesire este valoarea y;
functia utilizata (pe o
perioada) este: ![]()
Realizarea instrumentului virtual
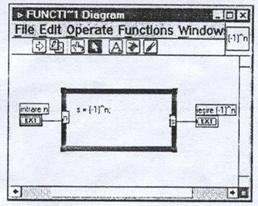
Realizarea instrumentului virtual se poate efectua in mai multe moduri. Astfel poate fi utilizata o structura de tipul ,,formula de calcul' sau numai functia ,,sinus'.


![]()
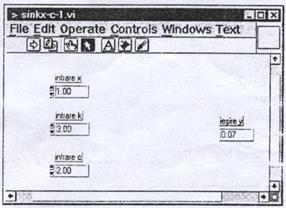
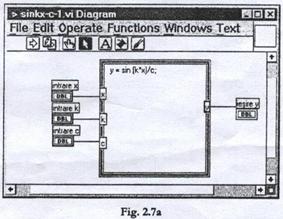
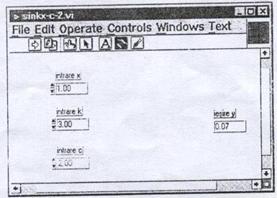
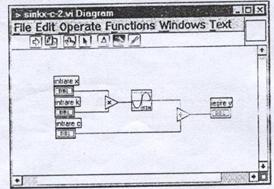
Cele doua instrumente virtuale sunt identice ca functionalitate si ca aspect al ferestrei panou, dar sunt diferite la nivelul ferestrei-diagrama.
Aceste instrumente virtuale pot fi incapsulate si inregistrate cu un simbol grafic. Daca se cere un astfel de instrument virtual, simbolul grafic poate fi vazut in fereastra de ajutor (help) ca in exemplul din Figura 2.8.

Cele doua instrumente virtuale create sunt identificate prin notatiile 1 si 2.
1.3. Sinteza semnalelor periodice
Realizarea unui program simplu
Sinteza semnalelor periodice este limitata in aceasta prima etapa la semnale cu doar trei armonici (primele trei). Se studiaza influenta acestor armonici in sinteza semnalului. Fereastra-panou care constituie interfata cu utilizatorul, va fi constituita din urmatoarele elemente: un ansamblu de 8 intrari numerice, care permit definirea coeficientilor k si c ai fundamentalei si ai celor trei armonici, precum si a unor iesiri grafice de tip osciloscop. Programul din fereastra-diagrama se realizeaza utilizand instrumentul grafic dezvoltat anterior. Pentru aceasta este suficient sa se introduca o structura respectiva de tip For (,,pentru") pentru crearea celor n puncte ale semnalului (Figura 2.9).

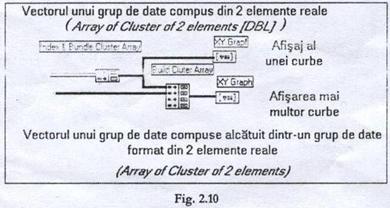
Pentru realizarea afisarii grafice a semnalului, se utilizeaza un obiect grafic din fereastra-panou de tip functie y = f(x), denumit XY Graph. Pentru a se putea afisa un semnal, este necesar sa se creeze un flux de date de intrare la nivelul ferestrei-diagrama, care sa fie compus din:
. un grup de date format din doi vectori: cluster of array;
. vector format dintr-un grup de doua date reale: array of cluster.
Pentru trasarea grafica este necesara functia descrisa prin:

Pentru a se putea afisa toate curbele obtinute pe acelasi grafic si pentru a studia evolutia constructiei semnalului se poate utiliza functia vectoriala :

Fluxul de date necesar reprezentarii grafice a unor curbe simple sau a unor curbe multiple cu un obiect grafic de tipul XY Graph este reprezentat in Fig. 2.10.
Se poate realiza un program mai simplu, fara utilizarea unei structuri de control repetitive, utilizand functia sin(x).

Programul realizat cu functia sinus este prezentat in figura 2. Programul se refera la sinteza semnalelor periodice cu trei armonice.
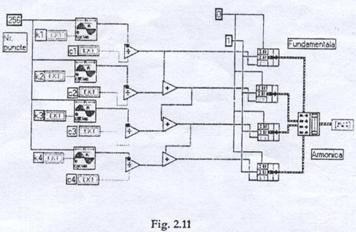
Curba semnalului in acest caz este afisata cu aparatul (obiectul) Waveform Graph, varianta Graph din lista de comenzi Controls din fereastra-panou.
Afisarea rezulta in urma crearii unui flux de date in fereastra-diagrama. Primele doua elemente ale fluxului de date sunt:
- valoarea primei abscise x0;
- valoarea pasului incremental Dx.
Fluxul de date poate fi construit pe baza:
- unui vector (primele doua elemente fiind x0 si Dx);
- unui grup de date compus din doua elemente simple (x0 si Dx) si un vector cluster of 3 elements.
In aceasta aplicatie se utilizeaza cea de-a doua solutie. Functia necesara pentru crearea fluxului de date este:

La fel ca in cazul aplicatiei precedente, pentru a se permite afisarea curbelor pe acelasi grafic si a studia astfel evolutia constructiei semnalului, se va utiliza o functie:

Fluxul de date din fereastra diagrama este prezentat in Figura 2.12; afisarea se realizeaza cu un obiect de tipul Waveform Graph, similar osciloscopului, ales cu comanda Graph din lista de comenzi Controls. Afisarea se poate efectua pentru una sau mai multe curbe simultan.
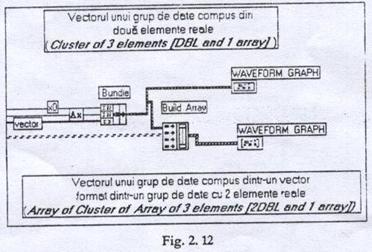
Studiul sintezei semnalelor periodice
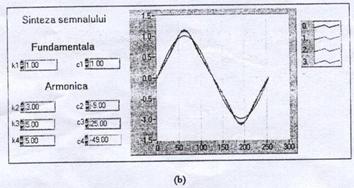
In cazul sintezei unor semnale dreptunghiulare sau triunghiulare, rezultatul poate fi vazut in Figura 2.13a si b.
Pentru semnalele dreptunghiulare este dificil de realizat sinteza numai cu primele trei armonici, intrucat acestea descresc cu 1/n.
Pentru semnalul triunghiular, armonicele scad in amplitudine mai evident (raportul 1/n2), iar elaborarea semnalului de sinteza este mai rapida.
Realizarea unui program complet de sinteza
In cazurile anterioare, sinteza semnalelor periodice s-a limitat numai la utilizarea primelor trei armonici. Pentru sinteza semnalelor periodice plecand de la un numar mai mare de armonici apare necesitatea calcularii coeficientilor Fourier in acelasi program.

Un asemenea program s-a realizat cu ajutorul a trei structuri de control ca in figura 2.14. In varianta a este sinteza semnalului dreptunghiular, iar in varianta b sinteza semnalului triunghiular.
Structurile de control utilizate sunt:
o structura de tratare Case pentru calculul coeficientilor in cazul semnalului dreptunghiular (cazul 1 Figura 2.14a) sau pentru calculul coeficientilor in cazul semnalului triunghiular (cazul 0 Figura 2.14b); se pot calcula coeficientii si pentru alte semnal daca se adauga alte cazuri la structura de tratare optionala.
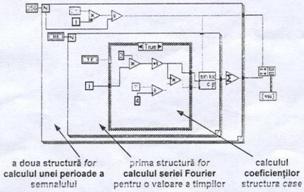
(a)

(b)
Prima structura repetitiva For: calculului seriei Fourier (pentru n termeni, coeficienti ai functiei sinus) pentru o valoare a timpului data
A doua structura repetitiva For destinata calcului unei perioade a semnalului
Pentru calcularea coeficientilor seriei Fourier al unui semnal triunghiular, trebuie creat un instrument virtual, pentru calculul expresiei (-1)n, adica:

Instrumentul virtual definitiv prealabil prin sin(kx)/c a fost utilizat impreuna cu operatorul de sumare a elementelor unui vector:

Sinteza celor semnale dreptunghiular si triunghiular realizata cu ajutorul calculului primelor 40 de armonici este prezentata in Figura 2.15a si b. Se remarca realizarea aproape ideala a celor doua semnale, cu exceptia celui dreptunghiular care are unele imperfectiuni in dreptul portiunilor tranzistorii.
Acest program de sinteza a semnalelor periodice poate fi aplicat si altor tipuri de semnale prin modificarea corespunzatoare a structurii de tratare optionala (Case).
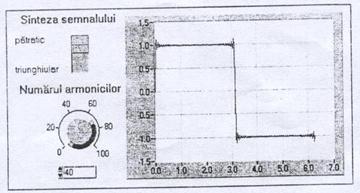
(a)
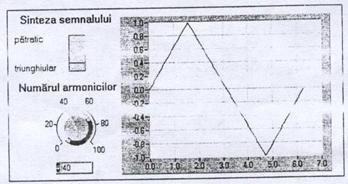
(b)
![]()
II.2. Analiza frecventiala si fereastra temporala
II.2.1 Elemente teoretice
Analiza frecventiala a semnalelor numerice si studiul ferestrei temporale are ca si scop:
calcularea transformatei Fourier discrete si utilizarea ei in cazul unui semnal sinusoidal pur (cu analiza influentei numarului de perioade, si a numarului de esantioane si cu evaluarea preciziei la nivelul spectrului frecventelor);
studiul efectelor diferitelor ferestre temporale: triunghi, Hanning, Hamming
Pentru calculul numeric al transformatei Fourier a unui semnal s(t), acesta este esantionat cu o perioada T si trunchiat temporal in vederea obtinerii unei serii de N termeni reprezentati prin;
![]()
cu termenii s(kTe), denumiti esantioane si d(t) denumit impuls Dirac.
Transformarea Fourier discreta (TFD sau DFT) a unui semnal definit de N esantioane este o serie de N termeni definita prin:
![]() cu
cu
![]()
Transformata Fourier discreta realizeaza o corespondenta intre doua ansambluri de N termeni, ca in exemplul din Figura 2.16.

II.2.2 Analiza frecventiala a unui semnal sinusoidal
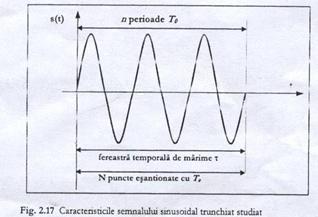
Daca se considera un semnal sinusoidal s(t)=sin(2pF0t), de perioada T0, limitat la n perioade, fereastra temporala a acestuia este o functie poarta numele de largime t. Acest semnal sinusoidal trunchiat este esantionat cu o frecventa Ft=1/Tt, conducand la N puncte de esantionare (Figura 2.17). Apare deci urmatoarea relatie intre parametrii ferestrei:
nT0=NTe=t
 c
c
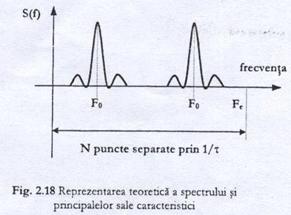
Intr-o reprezentare bilaterala, modulul spectrului semnalului sinusoidal este compus din doua impulsuri la frecventele -F0 si F0. Spectrul semnalului trunchiat prin fereastra temporala este format din doua functii sin c(p t) centrate pe frecventele -F0 si F0, ca in Figura 2.18. Functia sin c(p t) este spectrul semnalului "poarta" de largime t, care este folosit pentru trunchierea semnalului complet, limitat la n perioade.
Astfel, spectrul semnalului, format din N esantioane este calculat intre frecventele 0 si Ft ca in exemplul din figura 2.18. Punctele calculate ale spectrului sunt separate la distanta Df, care corespunde preciziei spectrului si se exprima sub forma:
![]()
Program simplificat de analiza spectrala a unui semnal sinusoidal
Un program de analiza spectrala a unui semnal sinusoidal are in Lab VIEW o fereastra panou sub forma prezentata in figura 2.19.

Se remarca in fereastra-panou:
doua intrari numerice: N-numarul de puncte si n - numarul de perioade
un indicator grafic pentru vizualizarea spectrului, gradat in ms;
un indicator grafic pentru vizualizarea spectrului, gradat in Hz.
Programul de analiza este compus din urmatoarele secvente:
sinteza semnalului sinusoidal anterior studiat;
calculul transformatei Fourier;
calculul modulului;
trasarea spectrului (amplitudinea maxima 1).
Pentru alcatuirea programului se folosesc urmatoarele instrumente virtuale:


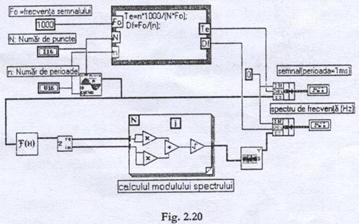
Programul de analiza spectrala a unui semnal sinusoidal este reprezentat in figura 2.20. Pentru afisarea curbelor cu abscise exprimate in milisecunde sau in Hz, se utilizeaza structura formule de calcul cu care sunt programate valorile Tt si Dj.
![]()
Constanta 1000 permite obtinerea unui rezultat in milisecunde.
Trasarea curbelor normalizate se realizeaza cu ajutorul urmatorului instrument virtual:

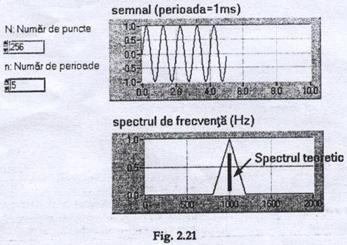
In figura 2.21 este prezentata fereastra panou in cazul analizei spectrale, unui semnal sinusoidal in cazul utilizarii a 256 de esantioane (N) si a 5 perioade (n). Spectrul teoretic este centrat pe frecventa semnalului (spectrul teoretic), dar curba rezultata nu corespunde unei functii de tipul sin c(p t). Acest lucru se explica printr-o discretizare in frecventa Df corespunzand la 1/t t fiind largimea ferestrei temporale).
Program complet de analiza spectrala a unui semnal sinusoidal
Pentru un program complet de analiza spectrala trebuie marita discretizarea in frecventa sau sa se utilizeze o fereastra temporala mai ingusta decat numarul de puncte de esantionare (vezi figura 2.22).

![]()
Ingustarea ferestrei este echivalenta cu lungirea semnalului cu valori nu ca in exemplul prezentat in figura 2.22. Se poate utiliza in program urmatorul instrument virtual de redimensionare:

Pentru utilizarea a doua astfel de instrumente virtuale se obtine divizarea cu 4 a preciziei in scara frecventelor.
Spectrul semnalului sinusoidal cercetat apare in fereastra-panou sub forma din figura 2.23.
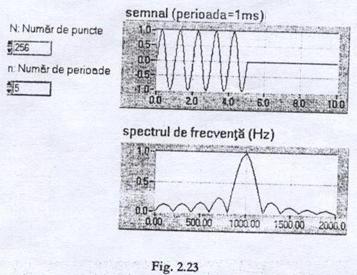
Programul (sau diagrama fluxului de date) din fereastra diagrama este prezentat in Figura 2.24.
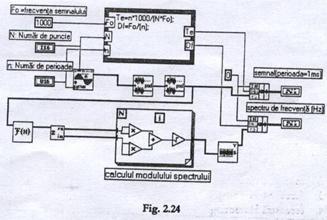
II.2.3 Studiul ferestrei temporale
Program de analiza spectrala realizat cu ajutorul unei ferestre temporale
Un program de analiza spectrala realizat cu ajutorul ferestrelor temporale are un continut asemanator programului aplicatiei precedente de analiza spectrala, deosebirea constand in adaugarea unei intrari numerice pentru a permite alegerea ferestrei.

Obiectul de intrare poate fi insotit de o eticheta Text Labels luata dintr-o lista de comenzi prezentata in Tabelul 1.9. Eticheta contine textele max si min in pozitiile extreme ale obiectului de intrare.
Modificarea textului unei etichete a unui obiect de tip intrare se face cu ajutorul unei liste de comenzi prezentata in Tabelul 2.1.
Obiectul de intrare utilizat in aceasta aplicatie are 4 intrari corespunzatoare celor 4 tipuri de ferestre temporale posibile.
fereastra naturala (poarta)
fereastra triunghiulara
fereastra Hanning
fereastra Hamming


Un program realizat cu ferestre temporale contine o structura de tratare optionala (case) comandata la intrare de 4 valori Alegerea ferestrei temporale: 1 pentru fereastra triunghi, 2 pentru fereastra Hanning si 3 pentru fereastra Hamming. In figura 2.26. este prezentat un program de analiza spectrala a unui semnal sinusoidal, cu alegerea ferestrei temporale triunghiulare. La alegerea cazului 0, structura optionala devine o simpla legatura intre intrare si iesire.
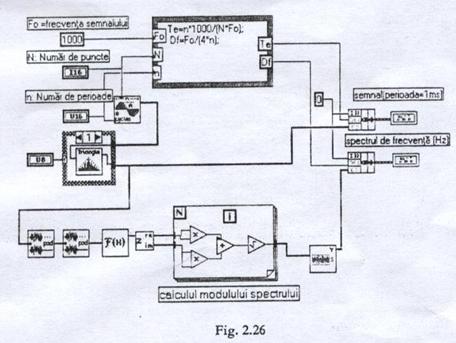
Analiza spectrala cu ferestre temporale diferite
Spectrul obtinut printr-o fereastra temporala naturala are abateri fata de spectrul teoretic. Pentru diminuarea abaterilor se pot utiliza ferestre triunghiulare, de tip Hanning sau de tip Hamming. Aceste ferestre atenueaza pana la suprimare lobii secundari si actioneaza asupra latimii lobului principal.
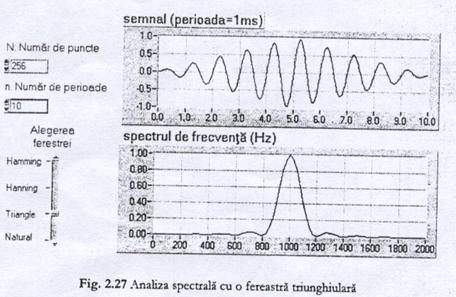
In conditiile utilizarii parametrilor N=256 si n=10, se pot observa efectele diferitelor ferestre. In figura 2.27. este prezentat efectul ferestrei triunghiulare in analiza spectrului.
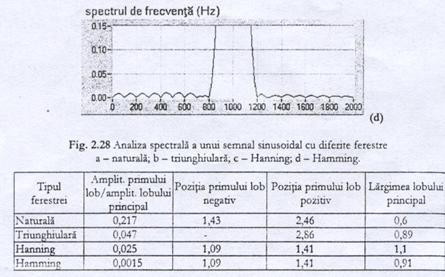
Pentru observarea unor modificari foarte mici se poate apela la vizualizarea detaliilor lobilor secundari cu ajutorul diferitelor ferestre, modificand scara axei ordonatelor ca in figura 2.28.
Rezultatele observarii sunt prezentate in tabelul 2.2.


II.3. Realizarea filtrelor numerice
II.3.1. Elemente teoretice
Studiul filtrarii numerice prezentat in continuare este realizat prin parcurgerea etapelor:
studiul raspunsului la impuls al unui filtru analogic trece-jos de ordinul 2;
realizarea unui filtru numeric corespunzator celui analogic, aproximat prin derivare si integrare.
Filtrele numerice sunt pentru semnalele esantionate, echivalentele filtrelor analogice pentru semnalele continue.
Programul LabVIEW are inglobate instrumente virtuale ce realizeaza filtrarea numerica, la care se poate accede prin comanda Filters din sublista de comenzi Analysis, a listei de comenzi Functions. Filtrele clasice disponibile sunt filtrul Butterworth, filtrul Cebisev, filtrul Bessel, filtrul eliptic si filtrul cu raspuns finit impuls (FIR: finite impulse response).
Pentru aceste filtre se pot defini parametrii de functionare cum ar fi ordinul filtrului, frecventa de taiere, castigul, etc.
Pentru realizarea unui filtru numeric se urmareste nu numai utilizarea celor existente, ci si construirea unui filtru specific trecand de la ecuatia sa.
Se numeste filtru numeric un procedeu de calcul (algoritm) care permite transformarea semnalului numeric (secvente de numere) intr-un alt semnal numeric in urma unei prelucrari sau modificari.
In cazul general al filtrelor numerice valoarea de iesire yk este functie de intrarea numerica xk din acelasi moment, de starea celor N intrari numerice precedente xk-i pentru iI si a celor N iesiri numerice precedente yk+i peniru iI. Un filtru numeric poate fi descris prin expresia:
yk=Function (xk-i, pentru iI, yk-j, pentru jI
Filtrele numerice sunt considerate in continuare liniare si invariante in timp, corespunzand filtrelor analogice descrise prin ecuatii diferentiale cu coeficienti constanti. Aceste sisteme numerice suni reprezentate prin ecuatii de recurenta numite ecuatii de diferente de forma:
![]()
Daca se aplica transformarea in z a ecuatiei precedente si daca Y(z) si X(z) sunt transformatele in z pentru xk si yk, rezulta:
![]()
Operatorul z-1 a transformatei in z se traduce printr-o intarziere de o unitate, adica esantionul xiz-1 corespunde esantionului precedent xi-1. Prin analogie cu filtrele analogice, un filtru numeric poate fi caracterizat prin functia de transfer in z sau transmitanta in z notata H(z):

Plecand de la expresia transmitantei in z a filtrului numeric, trebuie conceput algoritmul de calcul sau structura care permuta realizarea filtrului numeric.
Problema care apare consta in obtinerea unui H(z) pentru caracteristici bine definite (castig, faza, etc.) si corespunzand unui filtru analogic definit printr-o ecuatie diferentiala sau printr-o functie de transfer H(p) sau H(f). Metodele care permit determinarea ecuatiei diferentiale a filtrului sau a functiei de transfer H(p) sau H(f) raspunzand conditiilor de castig si faza sau unui raspuns la impuls, sunt cunoscute bine in cadrul filtrelor analogice.
Cel mai utilizat procedeu de sinteza a unui filtru numeric consta in transpunerea ecuatiei diferentiale a filtrului analogic. Transpunerea se poate efectua prin diverse metode, mai cunoscute fiind:
transformarea lui Euler sau aproximarea prin derivare;
transformarea homografica sau aproximarea prin derivare.
Transformarea lui Euler sau aproximarea prin derivatie
Daca se pleaca de la ecuatia diferentiala corespunzatoare filtrului analogic prin care sunt legate intrarea x(t) si iesirea y(t), operatiile de derivare succesiva se aproximeaza si se obtine ecuatia diferentelor corespunzatoare filtrului numeric. Aceasta metoda raspunde unei abordari clasice din analiza numerica, prin care se aproximeaza numeric derivata unei functii continue. In cazul transformarii lui Euler aceasta aproximare are forma:
![]()
in care Te este perioada de esantionare. Aceasta aproximare corespunde cu aproximarea calculului unei integrale prin metoda dreptunghiurilor.

Prin aceasta metoda se inlocuieste in functia de transfer H(p) operatorul Laplace p printr-o expresie prin care apare operatorul z-1 al transformatei in z:
![]()
Aceasta metoda de sinteza se aplica mai ales la simularea filtrelor analogice simple si prezinta adesea dezavantajul introducerii unei distorsiuni in domeniul frecventelor inalte.
Transformarea homografica sau aproximarea prin integrare
Ca si in cazul precedent, integrarea unei functii continue se aproximeaza numeric (metoda trapezelor):
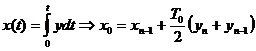
Aceasta metoda consta de asemenea in inlocuirea in functia de transfer de forma H(p) a operatorului Laplace p printr-o expresie in care intervine operatorul z' a transformatei in z.
![]()
Metoda de sinteza se aplica in mod special la simularea filtrelor analogice a caror caracteristica a frecventei este constanta in domeniul de frecventa dat. Filtrele numerice obtinute sunt in general foarte stabile.
II.3.2. Reprezentarea raspunsului teoretic al filtrului
Metoda utilizata pentru calculul raspunsului la impuls
In cazul unui filtru trece-jos analogic de ordinul 2, functia de transfer in domeniul frecventelor H(f) este sub forma urmatoare:
![]()
unde F0 este frecventa proprie a filtrului si m coeficientul de amortizare. Aceasta functie de transfer se obtine plecand de la ecuatia diferentiala de ordin doi a filtrului:
![]()
unde W pF0 este pulsatia proprie a
filtrului. Expresia precedenta a functiei de transfer poate sa
se exprime sub o forma mai compacta considerand raportul de
frecvente ![]() . Functia de transfer redusa H(R), devine:
. Functia de transfer redusa H(R), devine:
![]()
Plecand de la functia de transfer redusa
H(R), vom calcula raspunsul la impulsul redus b(r) a filtrului trece-jos
de ordinul doi, utilizand transformarea Fourier inversa F-1
[H(R)]=b(r). Acest raspuns este functie de raportul ![]() . Pentru a realiza acest calcul, se poate utiliza expresia
H(r) cu o parte reala Hr(R) si o parte imaginara Hi(R):
. Pentru a realiza acest calcul, se poate utiliza expresia
H(r) cu o parte reala Hr(R) si o parte imaginara Hi(R):

si
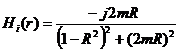
Realizarea programului
In fereastra-panou, programul contine:
doua intrari numerice: perioada proprie T0 a filtrului (exprimat in ms) si coeficientul de amortizare m;
doua iesiri diferite:
un indicator pentru afisarea frecventei proprii a filtrului F0 (=1/T0), in Hz;
un grafic prezentand raspunsul la impuls al filtrului in ms.
Programul de calcul al raspunsului la impuls al unui filtru analogic prezentat in figura 2.29. contine o structura "formula de calcul" prin care se pot obtine, plecand de la datele filtrului, partea reala si partea imaginara a expresiei H(R) conform relatiilor prezentate mai sus. Calculele sunt efectuate pentru N puncte, cu o structura de tipul For Loop. Instrumentul virtual "Transformata Fourier" permite apoi obtinerea raspunsului la impuls pe mai multe perioade, cu o scala gradata in ms.
Astfel se va tine cont de faptul ca:
pentru a realiza calculul functiei de transfer H(R), pentru un domeniu superior frecventei F0, este necesar ca R sa varieze intr-un domeniu [0,M] cu M>1. Pentru un calcul in N puncte, pasul de calcul pentru H(R) se ia DR=M/N cu M=N/F0, in conditiile in care F=F0, R=1 si DR=1 (pentru DF=1),
in
conditiile calcularii functiei H(R) pentru domeniul [0,M] si
cu pasul![]() R=M/N=1/F0, functia h(r) va avea domeniul [0,1/
R=M/N=1/F0, functia h(r) va avea domeniul [0,1/![]() R=F0] si pasul
R=F0] si pasul ![]() r=1/M=F0/N; daca se ia t=T0 cand
r=1 si T0
r=1/M=F0/N; daca se ia t=T0 cand
r=1 si T0![]() r/
r/![]() x=1, valoarea pasului
x=1, valoarea pasului ![]() x devine:
x devine:
![]()
in care T0 este in ms, iar F0 in Hz.
Aceste valori se calculeaza cu ajutorul celei de a doua structuri "formule de calcul". Inainte de calcularea transformatei Fourier inverse care necesita introducerea unui numar complex, se formeaza un vector complex pornind de la valorile Hr si Hi si utilizand instrumentul virtual de mai jos:
Raspunsul la impuls este afisat normalizat in amplitudine (valoarea maxima este 1).
In Figura 2.30. este prezentata curba de raspuns la impuls a unui filtru analogic de ordinul 2, cu o frecventa proprie de 50 Hz si un coeficient de amortizare cu valoarea 0,1. Curba corespunde unui regim de oscilatie amortizate.
II.3.3. Filtrul prin derivare
Calcularea filtrului numeric
Ecuatia filtrului numeric este o ecuatie diferentiala de aproximare prin derivare:
Yn =aYn-2 +bYn-1 +cYn
Coeficientii a, b, c se exprima nu numai in functie de parametrii filtrului (perioada proprie F0 si coeficientul de amortizare m) ci si in functie de perioada de esantionare Te :

luand D=1+4mpF0Te+(2pF0Te)2.
Pentru un exemplu de aplicatie (f0=50 Hz, m=0,1 si F0=500 Hz) valorile coeficientilor filtrului numeric sunt: a= -0,65770; b= 1,39805; c= 0,25965.
Realizarea programului
Pentru a realiza filtrul numeric se alege o structura de calcul repetitiv de tipul For Loop cu registre de decalare (SHIFT REGISTER) care permit sa se memoreze valorile precedente.
Memorarea celor 2 valori precedente se realizeaza cu un registru de decalare cu 2 elemente, ca in exemplul din Figura 2.31.
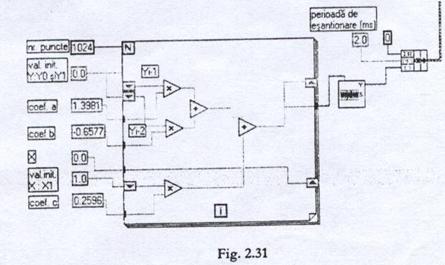
In figura apare programul de calcul pentru raspunsul la impuls al unui filtru numeric care simuleaza un filtru analogic de ordinul 2 aproximat prin derivare. Valorile initiale ale registrelor sunt nule; frecventa proprie este 20 Hz, iar perioada de esantionare de 2 ms.
Semnalul de intrare (impuls la t=0) este format cu ajutorul unui registru de decalare initializat la "1" si care furnizeaza un impuls cu amplitudinea "1".
Operatiile din structura repetitiva reproduc ecuatia diferentiala a filtrului cu coeficientii calculati anterior. Pasul de trasare grafica este egal perioadei de esantionare (2ms) pentru a avea un afisaj exprimat in ms si astfel comparabil curbei trasate pentru filtrul analogic.
Compararea rezultatelor filtrului numeric si ale filtrului analogic arata o diferenta de amortizare (Figura 2.32.)
Curba teoretica corespunzatoare filtrului analogic este trasata cu o linie continua, iar curba corespunzatoare filtrului numeric este trasata cu curba intrerupta. Diferenta se datoreaza aproximarii prin derivare.
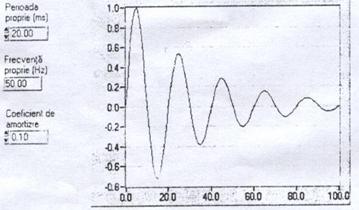
Fig. 2.32.
II. 3.4. Filtre aproximate prin integrare
Calcularea filtrului numeric
Ecuatia filtrului numeric se scrie sub forma:
Yn=aYn-2+bYn-1+cXn-2+dXn-1+eXn
coeficientii a, b, c, d, e se exprima in functie de aceeasi parametri; frecventa proprie F0, amortizarea m si perioada de esantionare Te.

unde D=4+8mpF0Te+![]()
In cazul unui exemplu cu f0=50 Hz, m=0,1 si F0=500 Hz valorile coeficientilor vor fi:
![]() a= -0,89181
a= -0,89181
b= 1,55193
c= 0,084971
d= 0,169942
e= 0,084971
Realizarea programului
Principiul realizarii acestui tip de filtru numeric este identic cu cel din exemplul anterior, utilizandu-se deci o structura repetitiva de tip For Loop cu registre de decalaj (SHIFT Register). In vederea memorarii valorilor precedente a lui Yn si Xn se utilizeaza 2 registre de decalare cu 2 elemente, pentru ca memorarea sa se realizeze pe 2 nivele ale indicelui buclei.
Valorile initiale ale acestor registre sunt puse pe 0 (Figura 2.33.). Semnalul de intrare este format in aceeasi maniera ca in exemplul precedent.

Se obtine un raspuns la impuls al unui filtru numeric echivalent cu al unui filtru analogic de ordinul doi. Aproximarea filtrului s-a realizat prin integrare. Frecventa proprie a filtrului este F0 este 20 Hz, amortizarea 0,1, iar perioada de esantionare de 2 ms.
Semnalul de intrare este format ca in exemplul prezentat in figura 2.33. In fig. 2.34. sunt prezentate comparativ raspunsurile filtrului numeric si al celui analogic.
Se observa o suprapunere a celor doua raspunsuri indicand realizarea unui filtru numeric foarte aproape de cel analogic. Curbele sunt vizualizate prin intermediul instrumentului virtual waveform graph din fereastra-panou, utilizand schema de program din figura 2.12.
|
Politica de confidentialitate |
| Copyright ©
2026 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |