
Ecuatiile de flux ale masinii asincrone
Fluxul din stator si cel din rotor reprezinta rezultatul comun al efectului tuturor curentilor din stator si din rotor. Intre rotor si stator exista o miscare relativa si deci inductivitatea mutuala dintre stator si rotor depinde de pozitia rotorului (unghiul dintre as si ar din fig. 2.1 si 2.2).
Vom considera o masina asincrona trifazata cu rotor bobinat si avand o distributie sinusoidala a campului, deci a curentului de-a lungul intrefierului.
Se considera de asemenea masina nesaturata (curba de magnetizare liniara). Fluxul magnetic total, care inlantuie o faza oarecare este determinat atat de sistemul trifazat de curenti statorici cat si de cei rotorici.
Vom avea astfel pentru stator fluxurile sa, sb, sc iar pentru rotor ra, rb, rc. Cu aceste valori instantanee se determina fazorul spatial de flux statoric s si de flux rotoric r (rel 1.9 si 1.19).
a) Tratarea cu fazori spatiali. Pentru fazorul spatial al fluxului total statoric in sistemul trifazat fix, atasat statorului,
![]() , (2.48)
, (2.48)
unde valorile instantanee ale componentelor variabile ale fluxurilor fazelor [21] sunt:
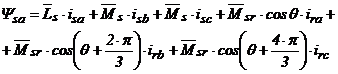 ; (2.49)
; (2.49)
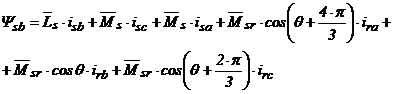 ; (2.50)
; (2.50)
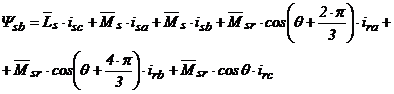 ; (2.51)
; (2.51)
In aceste ecuatii:
![]() este inductivitatea
proprie a unei infasurari de faza statorice;
este inductivitatea
proprie a unei infasurari de faza statorice;
![]() este inductivitatea
mutuala dintre infasurarile statorice;
este inductivitatea
mutuala dintre infasurarile statorice;
![]() este valoarea
maxima a inductivitatii mutuale dintre stator si rotor.
este valoarea
maxima a inductivitatii mutuale dintre stator si rotor.
Se poate observa ca fluxul variabil pe faza contine sase termeni de flux: o componenta a fluxului propriu produs de curentii statorici din infasurarea statorica luata in consideratie; doua componente de flux statoric mutual datorate celorlalti curenti statorici; trei componente de flux mutual dintre stator si rotor care sunt datorate celor trei curenti rotorici.
Inlocuind ecuatiile (2.49), (2.50), si (2.51) in ecuatia (2.48) si tinand seama de raportarea fazorului spatial al curentului rotoric (scris in sistemul atasat rotorului) la sistemul statoric fix, rezulta:
![]() . (2.52)
. (2.52)
In ecuatia (2.52):
![]() este inductivitatea trifazata totala a statorului;
este inductivitatea trifazata totala a statorului;
![]() este asa-numita inductivitate trifazata de
magnetizare.
este asa-numita inductivitate trifazata de
magnetizare.
In
ecuatia (2.52) fazorul spatial al fluxului statoric are doua
componente. Prima componenta, egala cu ![]() , este fazorul
spatial al fluxului propriu al fazelor statorice, cauzat de
curentii statorici. A doua componenta,
, este fazorul
spatial al fluxului propriu al fazelor statorice, cauzat de
curentii statorici. A doua componenta, ![]() , este un fazor
spatial al fluxului mutual, care se datoreste curentilor
rotorici si este exprimat in sistem trifazat fix.
, este un fazor
spatial al fluxului mutual, care se datoreste curentilor
rotorici si este exprimat in sistem trifazat fix.
Este important de observat ca ecuatia (2.52) este generala si se mentine chiar in conditiile circuitului magnetic neliniar. Astfel ea este valabila de asemenea cand circuitul magnetic este saturat. In acest caz Ls si Lm nu sunt constante si deci depind de curentii masinii [21].
Printr-un rationament analog rezulta fazorul spatial al fluxului total rotoric raportat la sistemul trifazat atasat rotorului:
![]() . (2.53)
. (2.53)
Pentru un sistem trifazat comun obtinem:
![]() ;
;
![]() ,
,
adica:
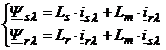 . (2.54)
. (2.54)
Inductivitatile totale trifazate ale statorului, respectiv rotorului se pot scrie:
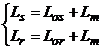 . (2.55)
. (2.55)
In aceste relatii:
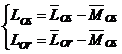 , (2.56)
, (2.56)
unde:
![]() reprezinta inductivitatea proprie de scapari a
unei faze a statorului, respectiv rotorului;
reprezinta inductivitatea proprie de scapari a
unei faze a statorului, respectiv rotorului;
![]() reprezinta inductivitatea mutuala de
scapari dintre doua faze statorice, respectiv rotorice.
reprezinta inductivitatea mutuala de
scapari dintre doua faze statorice, respectiv rotorice.
Inlocuind relatiile (2.55) in relatiile (2.54) si tinand seama de relatia (2.43) rezulta:
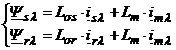 . (2.57)
. (2.57)
Notand fluxurile de scapari:
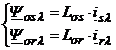 ;
;
si fluxul de magnetizare:
![]() ,
,
ecuatiile de flux devin:
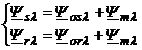 . (2.58)
. (2.58)
b) Scrierea matriceala in sistem trifazat a relatiilor (2.52) si (2.53) conduce la:
![]() .
.
Matricile
![]() si
si ![]() au fost introduse din
cauza pozitiei relative dintre cele doua sisteme de axe trifazate de
referinta la care sunt raportate marimile statorice, respectiv
rotorice, de pozitie variabila cu unghiul (fig. 2.2).
au fost introduse din
cauza pozitiei relative dintre cele doua sisteme de axe trifazate de
referinta la care sunt raportate marimile statorice, respectiv
rotorice, de pozitie variabila cu unghiul (fig. 2.2).
Eliminarea matricilor [T] are loc daca se raporteaza toate marimile la un sistem comun de axe trifazate determinat de unghiul , (rel. 2.35 si 2.36). Obtinem astfel:
![]() ,
,
![]() .
.
si deci:
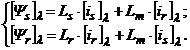 (2.59)
(2.59)
c) Scrierea matriceala in sistem bifazat comun rezulta, conform relatiei (1.28), din relatia (2.59) astfel:
![]() ,
,
respectiv,
![]() .
.
Rezulta:
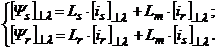 (2.60)
(2.60)
Tinand seama de (2.55) si (2.46), relatiile (2.60) se mai pot scrie:
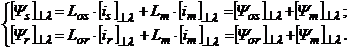 (2.61)
(2.61)
Ecuatiile de flux, indiferent de sistemul de axe d - q ales, nu isi modifica forma.
|
Politica de confidentialitate |
| Copyright ©
2026 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |