
Identitati algebrice booleene
In matematica, o identitate este o afirmatie valabila pentru toate valorile posibile ale variabilei sau variabilelor implicate. Identitatea algebrica x + 0 = x, ne spune ca suma dintre oricare variabila (x) si zero este egala cu variabila initiala (x), indiferent de valoarea acesteia. Asemenea algebrei obisnuite, exista identitati specifice algebrei booleene. Aceste identitati sunt bazate pe cele doua stari posibile ale variabilelor booleene (0 sau 1).
Prima identitate booleana este suma unei variabile cu zero. Rezultatul este valoarea variabilei initiale. Aceasta identitate nu este cu nimic diferita fata de echivalentul algebric al numerelor reale:
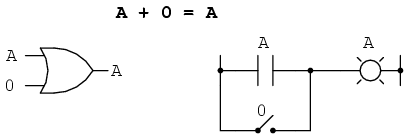
Indiferent de valoarea lui A, iesirea va fi tot timpul aceiasi. Cand A = 1, iesirea va fi 1; cand A = 0, iesirea va fi 0.
Urmatoarea identitate este cu siguranta diferita fata de cele vazute in algebra obisnuita. Aici putem vedea ca suma unei variabile cu 1 este 1:
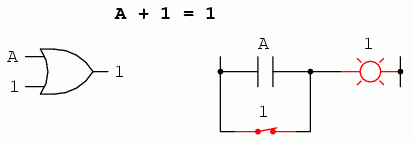
Indiferent de valoarea lui A, suma lui A cu 1 va fi tot timpul 1. Practic, iesirea circuitului nu tine cont de valoarea lui A, ci este fixata pe 1.
Urmatoare identitate este suma unei variabile cu ea insasi. Practic, acest lucru inseamna conectarea intrarilor unei porti logice SAU si activarea lor cu acelasi semnal:
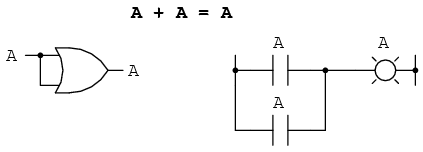
In algebra numerelor reale, suma a doua variabile identice este dublul variabilei initiale (x + x = 2x). Dar in cadrul algebrei booleene nu exista "2", ci numai 0 si 1. Prin urmare, nu putem spune ca A + A = 2A. Adunarea unei variabile cu ea insasi este egala cu variabila originala: 0 + 0 = 0 si 1 + 1 = 1.
Daca introducem conceptul de complement intr-o identitate aditiva, putem vedea un efect interesant. Din moment ce intre orice variabila si complementul acesteia trebuie sa avem un 1, si din moment ce suma oricarei variabile booleene cu 1 este 1, suma dintre o variabila si complementul ei trebuie sa fie 1:
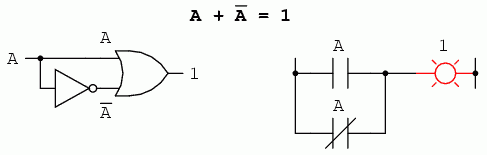
La fel cum exista patru identitati booleene aditive (A + 0, A + 1, A + A si A + A'), exista si patru identitati multiplicative: A x 0, A x 1, A x A si A x A'. Dintre acestea, primele doua nu sunt deloc diferite de identitatile echivalente ale algebrei numerelor reale:
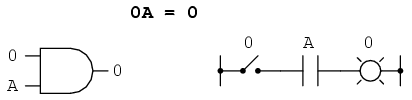
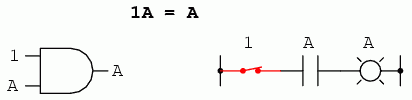
Cea de a treia identitate multiplicativa exprima rezultatul unei variabile booleene inmultita cu ea insasi. In algebra numerelor reale, acest tip de produs reprezinta patratul variabilei in cauza (3 x 3 = 32 = 9). Conceptul de "patrat" implica existenta valorii 2, valoare ce nu poate fi exprimata prin algebra booleana. Nu putem spune ca A x A = A2. In schimb, produsul unei valori booleene cu ea insasi este valoarea initiala, din moment ce 0 x 0 = 0 si 1 x 1 = 1:
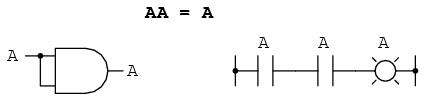
A patra identitate multiplicativa nu are echivalent in algebra numerelor reale, deoarece utilizeaza complementul variabilei. Acest concept este unic matematicii booleene. Din moment ce trebuie sa avem o valoare de "0" intre oricare variabila si complementul acesteia, si din moment ce produsul oricarei valorii booleene cu 0 este 0, produsul dintre o variabila si complementul acesteia trebuie sa fie 0:
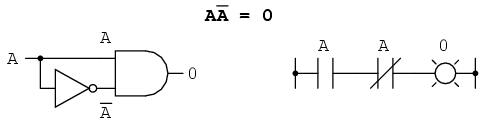
In concluzie, avem patru identitati booleene de baza pentru adunare si patru pentru produs (multiplicative):

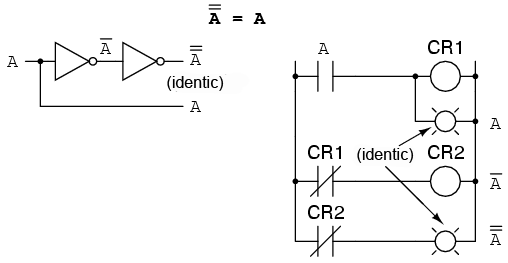
O alta identitate caracteristica complementului unei variabile este cea a complementului dublu: o variabila inversata de doua ori. Rezultatul complementarii duble a unei variabile este valoarea booleana initiala a variabilei. Acest lucru este similar inmultirii cu -1 in algebra numerelor reale: un numar par de astfel de inmultiri se anuleaza, iar rezultatul final este valoarea initiala:
|
Politica de confidentialitate |
| Copyright ©
2025 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |