
MECANICA SISTEMELOR DE ACTIONARE ELECTRICA
1.1. Generalitati
Intr-un sistem de actionare electrica (SAE) energia electrica activa este convertita de catre motorul de actionare in energie mecanica , care prin intermediul tranmisiei este cedata arborelui masinii, respectiv mecanismului de lucru in vederea efectuarii unor operatii impuse de procesul tehnologic. Procesele care au loc intr-un SAE sunt stabilizate, respectiv stationare in cazul in care marimile electrice si mecanice se mentin constante si sunt trazitorii daca marimile respective variaza in timp. In cazul unui regim tranzitoriu mecanic in schema principiala a unui SAE trebuie introdus un volant fictiv, care are momentul de inertie egal cu momentul de inertie echivalent (Je ) al partiilor componente ale intregului lant cinematic, redus la arborele motorului. Schema bloc principiala a partii mecanice a unui SAE este reprezentata in fig. 1.1.
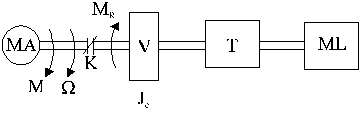
Fig.1.1. Schema bloc principiala a partii mecanice a unui SAE.
MA= motor de actionare, ML= mecanism ( masina) de lucru, K= cuplaj; T= trasmisie, V= volant.
Legea a doua a dinamicii aplicata unui SAE este cunoscuta sub numele de ecuatia fundamentala a miscarii:
![]() (1.1)
(1.1)
Daca se introduce cuplul dinamic expresia anterioara este :
Md = Je e
in care acceleratia unghiulara e este pozitiva in cazul accelerarii si negativa pentru decelerare (franare).
Pentru deplasari rectilinii s-au construit motoare electrice liniare. Sunt utilizate la puteri mari in tractiunea electrica de mare viteza. Ca masina electrica motorul liniar are un randament si un factor de putere mai mici decat un motor rotativ, dar pe ansamblul sistemului de actionare este superior pentru ca forta de tractiune se exercita direct asupra caii de rulare si totodata, se realizeaza o parte din forta de levitatie magnetica, care permite zborul magnetic controlat. Ecuatia miscarii liniare dedusa prin aplicarea legii a doua a dinamicii este :
![]() (1.2)
(1.2)
Forta dinmica care impune acceleratia liniara este: Fd = m.a
In ecuatiile (1.1) si (1.2) MR , respectiv FR sunt cuplul, respectiv forta rezistenta raportate la arborele masinii de actionare. Analog Je ,respectiv m sunt momentul de inertie, respectiv masa echivalenta raportate la arborele masinii de actionare.
In componenta unui SAE intra echipamentul electric compus din partea de forta, care executa controlul energiei electrice cu care este alimentata masina de actionare si partea de comanda, care proceseaza infomatia referitoare la conducerea SAE respectiv. In schema bloc principiala din figura 1.2 transmisia mecanica este reprezentata prin doua linii paralele continue, conexiunile electrice de forta printr-o singura linie continua, iar caile de transmitere a informatiei printr-o linie intrerupta.
Cerintele care se impun SAE actuale sunt in principal: robustetea, care include mentenabilitatea si fiabilitatea, reglarea fina a turatiei intr-o gama larga, utilizarea judicioasa a energiei electrice, care presupune un consum redus de putere activa, compensarea puterii reactive si reducerea puterii deformante.
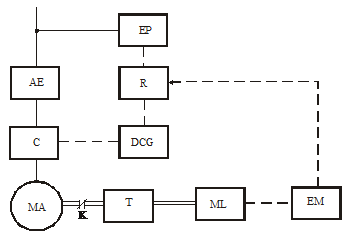
Fig. 1.2 Schema bloc principiala a unui SAE automatizat.
A= echipament electric de alimentare, C = convertor static, EM = element de masura, EP = element de prescriere, DCG = dispozitiv de comanda pe grila, R = regulator.
Dezideratele anterioare pot fi indeplinite de masina asincrona cu rotor in scurtcircuit si de masina sincrona excitata cu magneti permanenti, daca sunt alimentate prin convertoare de frecventa comandate numeric pentru a se realiza modulatia sinusoidala a impulsurilor.
O categorie aparte in cadrul sistemelor de actionare este formata din sistemele de pozitionare, la care bucla de reglare a vitezei de rotatie are suprapusa sau este inlocuita cu o bucla de reglare a pozitiei si din sistemele de urmarire. Acestea sunt echipate in general cu micromasini electrice speciale si trebuie sa indeplineasca indicatori statici si dinamici de calitate ai reglarii pozitiei performanti.
Ca pentru orice sistem electric de putere la SAE se pune problema compatibilitatii electromagnetice. Convertoarele cu tiristoare si masinile sincrone cu poli aparenti pot produce poluare sonora in domeniul audiofrecventelor, motiv pentru care trebuie luate contramasuri din faza de proiectare.
1.2. Analiza proceselor de miscare
1.2.1. Marimi si diagrame de miscare
Procesele de miscare se intalnesc in tehnica la o multitudine de masini de lucru, de exemplu:
- masini-unelte de: stunjit, frezat, gaurit, stantat, taiat, debitat;
- macarale, ascensoare, mijloace de transport;
- ventilatoare, pompe, compresoare;
- prese, valturi, calandre, masini de indoit si stantat.
Procesele de miscare cu o traiectorie impusa se numesc procese de pozitionare. Acestea se intalnesc la:
- ventile, impingatoare;
- manipulatoare, roboti, instalatii de pozitionare;
- linii tehnologice in tact, instrumente de urmarire
Procesele de miscare necesita energie mecanica, produsa prin conversia energiei electrice luata de la retea in convertoarele electromecanice (masinile electrice, electromagneti).
Tehnica actionarilor electrice trebuie sa rezolve urmatoarele sarcini:
- conversia electromecanica eficienta a energiei cu randament bun
- indeplinirea precisa a sarcinilor procesului tehnologic prin obtinerea marimilor mecanice: forta, respectiv momentul de rotatie si viteza
- controlul evolutiei marimilor mecanice in timp prin tehnica reglarii.
La alegerea si dimensionarea unui sistem de actionare electric pentru satisfacerea cerintelor anterioare trebuie cunoscute marimile cinematice prin efectuarea unei analize a procesului tehnologic.
Un corp punctiform prin deplasarea liniara sau circulara descrie spatiul:s = f (t). Relatiile de calcul si unitatiile de masura pentru marimile cinematice sunt date in tabelul de mai jos: In relatiile din tabele se fac particularizarile:
1. Miscare
uniforma: v, ![]() = constante
= constante
a, e
s, r
2. Miscare uniform accelerata:a, e = constante
s, r
3. Miscare uniform smuncita: s, r = constante.
Tabel 1.1. Marimi cinematice
a) miscare de translatie
|
Tipul marimii |
Relatia de calcul Prin derivare Prin integrare |
Unitatea de masura |
||
|
spatiu |
l |
|
m |
|
|
viteza |
|
|
m/s |
|
|
acceleratie |
|
|
m/s2 |
|
|
smuncitura |
|
m/s3 |
||
b)miscare de rotatie
|
Tipul marimii |
Relatia de calcul Prin derivare Prin integrare |
Unitatea de masura |
|
|
unghi |
a |
|
rad |
|
viteza unghiulara |
|
|
rad/s (1/sec) |
|
acceleratie unghiulara |
|
|
rad/s2 |
|
smuncitura unghiulara |
|
rad/s3 |
|
c) Relatii generale pentru calculul marimilor in intervalul de timp Dt cu variabile initiale: l0 , v0 , a0 .
|
Tipul marimii |
Relatia de calcul |
|
spatiu |
|
|
viteza |
|
|
acceleratie |
|
d) Relatii generale pentru calculul marimilor in intervalul de timp Dt cu variabile initiale: a w e
|
Tipul marimii |
Relatia de calcul |
|
unghi |
|
|
viteza unghiulara |
|
|
acceleratie unghiulara |
|
Smuncitura da incarcarea maxima a transmisiei mecanice si reducerea ei este importanta pentru comfortul calatorilor in cazul vehiculelor cu tractiune electrica. O smuncitura s > 2,5 m/s2 este neplacuta. Smucitura se poate diminua prin introducerea unui volant, care realizeaza o amortizare mecanica.
Diagramele de miscare liniara sunt valabile si la miscarea circulara (v = W R).
Problema este reprezentarea graficului de miscare in conditii initiale impuse de procesul de productie. Se cunosc sau se prescriu: lc , tc , v2 , a1 si se cer: t1 , t2 , t3 , l1 , l2 , l3 si a3 = a1 .
Cu considerarea vitezei medii in conformitate cu relatiile cunoscute din mecanica se obtin:
![]() ;
;![]() (1.3)
(1.3)
![]() ;
; ![]() ;
;  (1.4)
(1.4)
![]() ; l 2 = v2
t2; t3 = tc
- (t1 + t2);
; l 2 = v2
t2; t3 = tc
- (t1 + t2);
![]() (1.5)
(1.5)
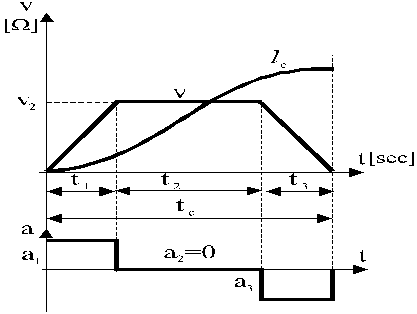 Fig.1.3. Diagrame de miscare liniara.
Fig.1.3. Diagrame de miscare liniara.
Criterii de optimizare: acelasi ciclu se poate efectua cu diferite acceleratii si viteze. Se pune problema realizarii ciclului cu durata minima. Parcurgerea lc in tmin cu acceleratie constanta, identica la pornire si oprire presupune realizarea unui grafic de viteze de forma unui trapez isoscel (t1 = t3). Suprafata trapezului isoscel din diagrama de miscare este egala cu spatiul parcurs .
![]() T
T![]() (1.6)
(1.6)
Durata minima a ciclului se obtine prin derivare in raport cu viteza:
![]() ;
; ![]() ;
; ![]() (1.7)
(1.7)
Marimile tc0 si v20 reprezinta baza si inaltimea triunghiului isoscel de suprafata l c egala cu a trapezului din care a degenerat.
![]() (1.8)
(1.8)

Fig.1.5. Diagrama cu ciclu minim.
Dezavantajul este ca sistemul functioneaza permanent in regim tranzitoriu, cu viteza variabila, deci este fie accelerat, fie decelerat. Se calculeaza raportul:
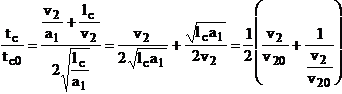 (1.9)
(1.9)
Se reprezinta grafic functia
![]() .
.

Fig.1.6. Durata ciclului in functie de viteza de mers stationar in diagrama trapez
Daca ![]() si
viceversa. Pentru
si
viceversa. Pentru ![]() rezulta
tc tc0
pentru ca
rezulta
tc tc0
pentru ca
![]() . In concluzie pentru reducerea lui tc se recomanda
o viteza
de mers stationar
de: v = (0,3 - 0,4) v20 .
. In concluzie pentru reducerea lui tc se recomanda
o viteza
de mers stationar
de: v = (0,3 - 0,4) v20 .
La
vehicule pentru transportul de persoane trebuie atenuate smunciturile. Experienta
arata
ca
senzatia
neplacuta
se datoreaza
acceleratiei
variabile. Prin definitie smuncitura (tab.1.1) este: ![]() . (1.10)
. (1.10)
Pentru digramele de miscare la care viteza variaza sub forma unui trapez (fig.1.3) smuncitura ia valorile:
pt.
t = 0 T ![]() ;
;
pt.
t = t1 T ![]()

Fig.1.7. Pornirea cu variatia trapezoidala a acceleratiei
Acceleratia variaza in treapta: pozitiva sau negativa. Practic jocurile si elasticitatea sistemului nu permit valori nedeterminate ale smuciturii (s = ), dar totusi aceasta este puternica.
Pentru reducerea smunciturii in procesul tranzitoriu de pornire acceleratia poate varia dupa o diagrama sub forma de trapez isoscel sau de sinusoida.
In primul caz:
v = a (t) t = k t2 , a (t) = k t T ![]() (1.11)
(1.11)
In consecinta smuncitura va avea o valoare finita.
Aplicatia 1.1. Intr-un bloc cu apartamente inaltimea dintre etaje este de 6 m. Liftul nu trebuie sa depaseasca valorile maxime: sm = 2,4 m/s3 ; am = 1,5 m/s2 ; vm = 2,1 m/s .
Sa se determine variatia marimilor in timp la parcurgerea spatiului dintre etaje.
Rezolvare: Primul interval este de accelerare cu smucitura.
![]() ; a1
= am .
; a1
= am .
Se determina spatiul si viteza:
![]()
![]()
In al doilea
interval apare o miscare uniform accelerata,
pentru a atinge vm . 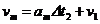 ;
;
![]()
![]()
Urmeaza o miscare deccelerata cu soc de semn contrar celui din intervalul t1 (Dt3 = 0,625 s).

![]()
![]()
Se obtine v3 > vmax . Este necesar un calcul iterativ pentru reducerea vitezei(v2 < vmax ). Se impune:
![]()
v2 = 2,1 - 0,468 = 1,632 m/s
Se reface calculul pentru intervalul 2.
![]()
![]()
Spatiul pentru intervalul 3 este:
![]()
In intervalul 3-4 se efectueaza deplasarea cu miscare uniforma, iar in intervalele 4-5, 5-6, 6-7 se repeta operatiile din intervalul 0-3 cu acceleratie de semn opus. Spatiul parcurs in miscarea uniforma este:
l 4 = l t -2 l 3 = 6 - 2 1,832 = 2,336 m
![]()
Timpul de efectuare a deplasarii intre doua etaje este:
![]()
Diagrama marimilor s, a, v, l pe intervale de timp este reprezentata in figura A 1.1.

Fig.A.1.1.Diagrame de miscare
Aplicatia 1.2. Sa se determine diagramele de miscare pentru o variatia sinusoidala a acceleratiei. Orientativ se pot considera datele de la aplicatia anterioara.
1.2.2 Ecuatia miscarii
Principiul conservarii energiei in miscarea de rotatie impune : Mdα = Wc.
Prin derivare in raport cu timpul se obtine echilibrul puterilor.

Fig.1.8. Mecanica sistemului de actionare electrica
![]()
![]() (1.13)
(1.13)
In majoritatea cazurilor practice J = constant. In consecita relatia (1.13) devine ecuatia fundamentala a miscarii:

Daca M, W au acelasi sens rezulta acceleratie, iar daca M, W au sensuri contrar rezulta decceleratie. Cuplul rezistent (MR) poate fi de doua tipuri:
reactiv: daca este de frecare, deformare plastica, iar efectul este de franare pentru ca actioneaza in sens contrar miscarii;
potential: se datoreste actiunii campului gravitational sau deformarii elastice a metalelor si nu depinde de sensul miscarii.
De exemplu pentru mecanismul de ridicare-coborare (fig.1.9) cuplul rezistent este de ambele tipuri:
MR = MRr + MRp
Pentru:
1) M > MR rezulta
![]() accelerare
accelerare
2) M = MR rezulta
![]() , deci W este constant, iar regimul
este stabilizat;
, deci W este constant, iar regimul
este stabilizat;
3) M < MR rezulta
![]() , decelerarie (franare).
, decelerarie (franare).
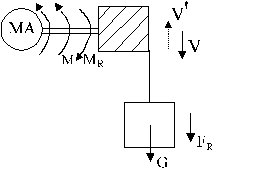
Fig.1.9.Echilibrul cuplurilor la mecanismul de ridicare - coborare
La sistemele cu miscare de translatie ecuatia miscarii se poate exprima in puteri sau forte:
![]()
![]() (1.15)
(1.15)
Uzual m = constant, caz in care rezulta:
![]() (1.16)
(1.16)
Momentul de inertie al unui corp fata de o axa de relatie care trece prin centru de greutate este:
![]() (1.17)
(1.17)
![]() (1.18)
(1.18)
daca masa elementului de volum este dm sau la o repartizare discreta mx a acesteia.
Considerand masa m concentrata intr-un punct la distanta r de axa de rotatie
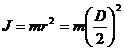 ; G = m g;
; G = m g;![]() G D2 = 4 g J (1.19)
G D2 = 4 g J (1.19)
Produsul GD2 se numeste momentul de giratie sau de
volant si
este dat in
cataloage pentru masinile electrice. Viteza de rotatie
se poate exprima in
functie
de turatie:
![]() (1.20)
(1.20)
In calculele practice se poate utiliza ecuatia miscarii sub forma:
![]() (1.21)
(1.21)
1.2.3. Raportarea cuplurilor si fortelor la arbore
Raportarea trebuie sa respecte principiul conservarii energiei. Arborele de raportat este cel motor, deci al masinii de actionare.Prezenta transmisiei (T) este impusa de faptul ca turatia masinii de actionare este mult mai mare decat turatia masinii de lucru, deci trebuie montat un reductor in mai multe trepte. Se considera de exemplu un reductor cu n trepte, reprezentat in fig.1.10.
Cuplurile determinate de masina de lucru raportate la arborii 0, 1, , n, care au vitezele W Wn , sunt :MR , MR1 , , MRn , iar momentele de inertie sunt : J1 , , Jn . Rapoartele de transmisie intre trepte (de ex. de la un angrenaj cu roti dintate) sunt i1 , , in si randamente h hn
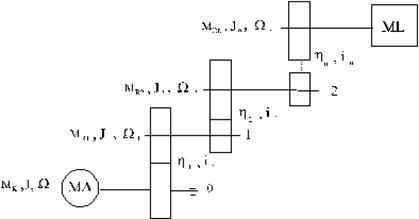
Fig.1.10. Transmisie cu n trepte.
Se determina randamentul global si raportul total de transmisie:
h h h hn
![]() ;
; ![]() ; ;
; ;![]() ;
; ![]() (1.22)
(1.22)
Se egaleaza puterile la arbori succesiv in ipoteza ca masina electrica functioneaza in regim de motor.
![]() T
T ![]() (1.23)
(1.23)
Celelalte cupluri rezistente se calculeaza cu relatii similare:
![]() ; ;
; ; ![]() (1.24)
(1.24)
Inmult
 (1.25)
(1.25)
La franare se inverseaza fluxul de energie.
![]() (1.26)
(1.26)
Unele utilaje, de ex. raboteze, poduri rulante, ascensoare, macarale au componente mecanice cu miscare de translatie:. Schema unui mecanism de ridicare cu transmisie (z) si tambur (T) este data in figura urmatoare. Ridicarea unei greutati G -= FR cu tamburul T impune egalitatea puterilor.
![]() (1.27)
(1.27)
Cuplul redus la arborele motor este : ![]() (1.28)
(1.28)

Fig.1.11. Transmisia la un mecanism de ridicare.
La coborare in regim stabilizat masina electrica franeaza suprasincron pierderile fiind acoperite de masina de lucru:
![]() (1.29)
(1.29)
1.2.4. Raportarea momentelor de inertie si a masei la acelasi arbore
Din conservarea energiei cinetice raportul momentelor de inertie J1 , J2 , , Jn la arborele masinii de actionare se face considerand un moment de inertie echivalent Je corespunzator unui dispozitiv numit volant.
![]() (1.30)
(1.30)
 (1.31)
(1.31)
![]() (1.32)
(1.32)
In cazul mecanismelor cu miscare de translatie:
![]()
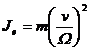 (1.33)
(1.33)
Expresia generala a momentului de inertie echivalent se obtine prin insumare:

Mecanismul biela-manivela este utilizat pentru transformarea miscarii de rotatie in miscare de translatie; se aplica la compresoare, locomotivele cu aburi, etc.
Aplicatia 1.3. Sa
se determine expresia cuplului rezistent opus de mecanismul
Rezolvare:
Cuplul masinii de lucru
raportat la axa manivelei (axa 0) este: MR0 = Ft r
, iar la arborele masinii electrice: ![]() .
.

Fig. A1.2. Descompunerea fortelor
la mecanismul
Forta tangentiala si cuplul rezistent au expresiile:
![]()
![]()
Din triunghiul OAB se determina sinb in functie de sina
![]() ;
; 
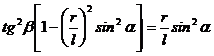 ;
;

Cuplul rezistent este dat de relatia:


Daca:
![]() T b
T b
Cuplul rezistent al mecanismului redus la arborele motorului de actionare are o variatie sinusoidala in functie de unghiul de pozitie al manivelei:
Aplicatia 1.4: Sa se calculeze expresia momentului de inertie echivalent pentru mecanismul biela-manivela, cu elementele geometrice date.
1.2.5. Stabilitatea statica a actionarilor electrice
Punctul de functionare static se gaseste la intersectia caracteristicilor mecanice a masinii de actionare si a masinii de lucru si corespunde unei functionari stabile sau instabile. Exprimarea a stabilitatii statice se poate face grafic sau analitic.
a. Exprimarea grafica a stabilitatii statice:
Se defineste ca sistemul de actionare electrica functioneaza stabil in punctul A daca la aparitia unei mici perturbatii punctul de functionare se stabileste intr-un punct de functionare A' apropiat de A; iar WA WA'
Se mentioneaza ca stabilitatea se numeste statica pentru ca functionarea are loc pe caracteristicile mecanice statice.Perturbatii care pot apare sunt variatia tensiunii la borne, a frecventei, a rezistentelor infasurarii masinii, a cuplului rezistent.
Sa presupunem ca A este punctul de functionare statica. Apare o perturbatie de incarcare care modifica caracteristica mecanica a masinii de lucru din (1) in (2). Caracteristica mecanica a masinii de actionare este reprezentata prin curba (3), de ex. pentru o masina asincrona. Datorita inertiei mecanice viteza de rotatie (W ) ramane constanta. Punctul de functionare se muta din (A) in (B) unde MRB > MA . Prin urmare viteza va scade pana la W corespunzatoare punctului A', pentru care MA' = MRA' .Deci apare un nou punct de functionare stabil.
In schimb punctul C caracterizeaza o functionare instabila. La aparitia perturbatiei W ramane constanta datorita inertiei, dar MRD > MC , deci sistemul va frana pana la oprire pentru ca M < MR pe tot intervalul.
Concluzie: Stabilitatea statica pentru un sistem de actionare electric este proprietatea acestuia de a reveni la un echilibru stabil intr-un interval de timp cat mai scurt dupa ce a fost scos din acesta datorita variatiei fie a lui MR si/sau a lui M.
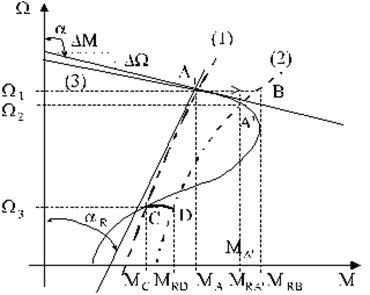
Fig.1.12.Determinarea grafica a stabilitatii statice
b.Exprimarea analitica a stabilitatii statice
La aparitia perturbatiei au la urmatoarele variatiiale cuplului motr, rezistent si ale vitezei de rotatie: M M+DM , MR MR +DMR , W W DW
Ecuatia miscarii este:
![]() (1.35)
(1.35)
![]() (1.36)
(1.36)
Sa consideram intervale de timp foarte scurte in care M, MR W
![]() (1.37)
(1.37)
in care:
![]() (1.38)
(1.38)
![]() (1.39)
(1.39)
![]() (1.40)
(1.40)
Se noteaza: tg a - tg aR = e si se numeste coeficient de stabilitate statica.

![]() ;
;![]() T (1.41)
T (1.41)
t = 0; DW DWi
Concluzie: Pentru functionarea stabila trebuie ca variatia de viteza sa fie cat mai mica (DW = 0, pentru ca J, t > 0). In consecinta trebuie ca e< 0.
Caz particular:
- pentru MR = constant rezulta tg aR = 0, deoarece e < 0 trebuie ca tg a < 0. Deci a > 900 adica caracteristica W (M) trebuie sa aiba alura cazatoare.

(1.42)
Pentru dW > 0 rezulta dMJ < 0, deci la cresterea vitezei trebuie ca MJ sa scada si viceversa., iar pentru dW < 0 rezulta dMJ > 0.
1.2.6 Stabilitatea dinamica
Perturbatiile sau variatia unor marimi din sistemul de actionare electrica pot determina variatii rapide ale M si/sau MR. Punctul de functionare se deplaseaza pe o traiectorie dinamica in functie de inertia electromecanica si electromagnetica a sistemului de actionare electrica.
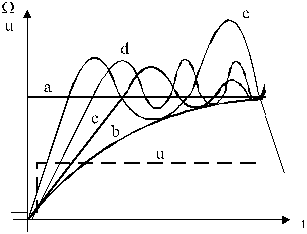
Fig.1.13. Stabilitatea dinamica a SAE.
a - sistem ideal fara inertie W (t) urmareste variabila treapta
b - proces aperiodic
c - W (t) oscileaza amortizat
d - W (t) oscileaza neamortizat, situatie defavorabila
e - W (t) oscileaza cu amplitudini crescatoare, situatie inadmisibila.
Calitatea sistemului de actionare electrica se poate aprecia prin modul in care sistemul raspunde la semnal treapta. De exemplu in figura urmatoare semnalul treapta este variabila u (t), iar marimea de iesire este W (t) pentru o masina de curent continuu. Parametrii sistemului de actionare se calculeaza pentru a se obtine un proces ai carui parametrii variaza tranzitoriu amortizat.
1.2.7. Metode de rezolvare a ecuatiei de miscare
1.2.7.1. Generalitati
Procesele tranzitorii: determina consumul de energie, productivitatea, randamentul, solicitarea electromagnetica si termica a sistemului de actionare electrica, deci conditiile de proiectare.
Se deosebesc trei tipuri de procese tranzitorii caracteristice fiecare printr-o constanta de timp, cu valori de ordine de marime diferita.
1. Inertia
electromagnetica
se datoreaza
inductivitatii
infas![]() .
.
2. Inertia mecanica
se caracterizeaza
prin
![]() (1.43)
(1.43)
sN= alunecarea nominala.
3. Inertia
termica
este caracterizata
de ![]() (1.44)
(1.44)
|
Politica de confidentialitate |
| Copyright ©
2025 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |