
Initial, baza de cunostinte nu contine informatii. Acestea sunt achizitionate in timpul fazei de instruire, prin adaugarea de noi celule de baza la fiecare moment de esantionare. Structura initiala a bazei de cunostinte contine radacina Tr a raspunsurilor in timp, radacinile Cp,q ale listelor de clasa, o radacina a listei celulelor de baza libere si o radacina a listei celulelor lista libere. Cand se incarca o celula de baza, aceasta este aleasa din lista celulelor libere. Daca o celula din structura este stearsa, ea se reintoarce in lista libera. Alegerea semnalelor de invatare si setarea parametrilor de instruire sunt prezentate mai tarziu.
Se presupune ca toate celulele de baza ce vor fi utilizate in sistem sunt initial incluse in lista de celule de baza libere. Daca in constructia bazei de cunostinte este necesara o celula de baza, ea este aleasa din lista celulelor libere. Daca o celula de baza din structura de cunostinte este stearsa, ea se reintoarce in lista libera. Suma intre CB utilizate si CB din lista libera este constanta si valoarea ei este aleasa de catre proiectant. Afirmatia este valabila si pentru celulele lista.
In timpul fazei de invatare, incarcarea unei noi celule de baza CBj implica stocarea valorilor CBj_u si CBj_y, reprezentand respectiv intrarea u(k) si iesirea y(k) a procesului la momentul de esantionare k si conectarea celulei cu structura initiala (cu alte celule din baza) prin relatii in timp si in spatiu, prin definirea valorilor operatorilor predecesor si succesor. Daca celula este prima dintr-un raspuns, lista raspunsurilor in timp trebuie sa fie extinsa. Prin adaugarea unei noi celule, anumite valori ale operatorilor deja stocate in baza vor trebui modificate. Ultima CB a raspunsului in timp curent se obtine aplicand operatorul ST unui obiect Tl, definit similar cu o radacina. In mod similar, ultima celula a unui raspuns se obtine aplicand operatorul SL unui obiect Ll. Aplicarea operatorului SC unui al treilea obiect Cr indica prima celula dintr-o lista de clasa.
Algoritmul de constructie al structurii de cunostinte va functiona astfel:
In ambele cazuri
Ia o celula de baza libera CBj si seteaza toate campurile ei cu 0.
Cazul 1 (noua celula este prima dintr-un raspuns in timp) - se ia o celula lista libera CLl si se seteaza toate campurile cu 0.
Cazul 1a: Daca (SL Tr) = 0 (nu au fost stocate in baza momente de esantionare anterioare), noua CLl se conecteaza la radacina Tr: (SL Tr) = CLl.
Cazul 1b: Daca (SL Tr) 0 (in baza a fost stocat cel putin un moment de esantionare anterior), noua celula CLl se conecteaza la sfarsitul listei cu celule lista deja construita. Daca ultima celula din aceasta lista era CLi , apar noi relatii : (SL CLi) = CLl si (PL CLl) = CLi.
In ambele subcazuri, celula lista este conectata cu celula de baza ((CB CLl) = CBj), iar Ll va indica noul raspuns in timp: (SL Ll) = CLl..
Cazul 2 (noua celula nu este prima dintr-un raspuns in timp) - se construiesc relatiile in timp (ST CBm) = CBj si (PT CBj) = CBm, presupunand ca CBm era ultima celula de baza a raspunsului in timp curent: CBm = (ST Tl).
In ambele cazuri: Se incarca in noua celula informatiile de proces la momentul de esantionare k: CBj-u = u(k) si CBj-y = y(k), iar Tl indica noua celula: (ST Tl) = CBj.
Constructia relatiilor in valoare: Se determina clasa celulei: Cp,q = C(CBj) si este cautata lista de clasa respectiva.
Daca (SC Cr) = 0, nu exista o lista de clasa corespunzatoare, Cp,q devine o noua lista de clasa (cu o unica celula CBj)si constructia relatiilor in valoare este terminata.
Daca (SC Cr) , exista deja o lista de clasa a carei prima celula este CBn = (SC Cr) si noile relatii in valoare sunt (SC CBj) = CBn si (PC CBn) = CBj.
Procedura iterativa prezentata mai sus permite constructia din aproape in aproape a structurii de cunostinte ce va fi utilizata mai departe pentru sinteza unui model si a unui controler fuzzy.
Teoria sistemelor recomanda, in cazul proiectarii analitice a unui sistem de reglare automata, compararea raspunsurilor prin utilizarea unui criteriu integral patratic. In cadrul metodei de proiectare cu structuri celulare propusa, aceasta comparatie se face pe o cale asemanatoare rationamentului uman, urmarindu-se obtinerea unei masuri a similaritatii care sa exprime gradul de asemanare intre doua raspunsuri in timp. Aceasta masura va avea valori continui cuprinse intre 0 si 1, ca si cum ar fi vorba de o apreciere umana si se executa utilizand teoria multimilor fuzzy. Rezultatele vor fi folosite mai departe in constructia modelului si a controlerului fuzzy. Comparatiile vor fi de doua tipuri: intre raspunsul la momentul si un raspuns din baza de cunostinte sau intre doua raspunsuri din baza de cunostinte.
In cele ce urmeaza, procesul luat in considerare este monovariabil, presupus cauzal si invariant in timp, de tipul:
![]() (5.16)
(5.16)
unde u(k) si y(k) reprezinta intrarea, respectiv iesirea procesului la momentul actual de timp kTs, iar n desemneaza adancimea trecutului luat in considerare, exprimata in numar de perioade de esantionare.
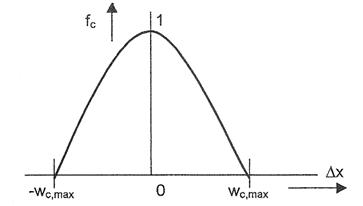
Figura III.49. Multimea fuzzy de comparare
Similaritatea se
exprima printr-o valoare numita masura
fuzzy a similaritatii, obtinuta cu ajutorul unor multimi fuzzy de comparare ![]() , convexe si normalizate. Vom avea o functie fc,u pentru
diferentele Du in u
si o functie fc,y pentru diferentele Dy in y. In
Figura III.49, Dx desemneaza
diferentele Du sau Dy. Alegerea multimii fuzzy de comparare depinde
de volumul de informatii din baza de cunostinte. Daca sunt
stocate numai cateva raspunsuri, multimea trebuie sa fie
larga, altfel sansa ca doua raspunsuri sa semene este
foarte mica. Largimea nu poate fi totusi oricat de mare, pentru
ca se poate ajunge la imposibilitatea separarii raspunsurilor. Daca in baza de
sunt stocate mai multe raspunsuri, se poate utiliza o multime fuzzy
mai ingusta, fara a se diminua performantele finale ale
sistemului.
, convexe si normalizate. Vom avea o functie fc,u pentru
diferentele Du in u
si o functie fc,y pentru diferentele Dy in y. In
Figura III.49, Dx desemneaza
diferentele Du sau Dy. Alegerea multimii fuzzy de comparare depinde
de volumul de informatii din baza de cunostinte. Daca sunt
stocate numai cateva raspunsuri, multimea trebuie sa fie
larga, altfel sansa ca doua raspunsuri sa semene este
foarte mica. Largimea nu poate fi totusi oricat de mare, pentru
ca se poate ajunge la imposibilitatea separarii raspunsurilor. Daca in baza de
sunt stocate mai multe raspunsuri, se poate utiliza o multime fuzzy
mai ingusta, fara a se diminua performantele finale ale
sistemului.
Este recomandabil ca alegerea largimii multimii fuzzy sa fie dependenta de cantitatea de informatii disponibila la un moment dat, adica sa fie modificata la fiecare moment de esantionare. Pentru asta, multimea de comparare este extinsa intr-o clasa a multimilor fuzzy de comparare, fc,e.

Figura III.50. Clasele multimilor fuzzy de comparare
O posibila alegere a
clasei este ![]() , unde e se numeste extensia (largimea) functiei.
, unde e se numeste extensia (largimea) functiei.
Pentru un proces liniar descris de ecuatia (5.16), raspunsul la un anumit moment poate rezulta prin inmultirea unui raspuns deja stocat cu un factor de liniarizare g:
![]() (5.17)
(5.17)
Relatia (5.17) arata ca nu este necesar sa se memoreze toate raspunsurile cu aceeasi forma, deoarece sistemul se comporta identic la toate intrarile care difera numai in amplitudine. Prin conventie, vom multiplica cu factorul g numai raspunsurile din baza de cunostinte, nu si pe cele actuale. Daca procesul este neliniar, formula (5.17) este doar aproximativa si factorul de liniarizare g va fi restrictionat printr-o valoare limita de prag, gb, conform conditiei:
![]() (5.18)
(5.18)
Pentru a alege valorile
factorilor de liniarizare se utilizeaza o multime fuzzy ![]() , numita
masura fuzzy a liniaritatii, cu urmatoarele
proprietati:
, numita
masura fuzzy a liniaritatii, cu urmatoarele
proprietati:
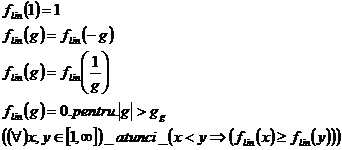 (5.19)
(5.19)
Multimea flin se alege astfel incat valoarea g=1 sa fie considerata total satisfacatoare, iar valorile diferite de 1, partial satisfacatoare. Asemanarea intre doua raspunsuri este cu atat mai buna cu cat |g| se apropie de 1.
In general, iesirea neperturbata a procesului depinde in mod diferit de valorile lui u si y la momentele anterioare de esantionare, ceea ce sugereaza ideea de a aloca ponderi, sub forma unor valori de apartenenta, fiecarui moment de esantionare. Fiecare pondere - relativa la un moment de esantionare ales ca etalon - indica cat de mult pot fi luate in considerare pentru calculul similaritatii valorile u si y din acel moment, adica importanta relativa a momentului de esantionare in procesul de comparare al raspunsurilor. Numai primele np ponderi, referitoare la np momente de esantionare din trecut, vor fi diferite de 0. Multimea ponderilor f0 se numeste multime fuzzy ordin iar np se numeste simplu ordin:
![]()
Alocarea ponderilor nu este restrictionata de adancimea evaluarii in trecut si este posibil ca f0(j) > f0(i), pentru j > i. Daca multimea fuzzy ordin se poate calcula, ea devine o masura fuzzy a ordinului, fm0 .
Evaluarea prin comparatia a doua raspunsuri este diferita in functie de aplicatie. Daca sistemul este utilizat ca un model fuzzy, numai trecutul raspunsului actual este comparat cu trecutul raspunsurilor din baza de cunostinte, pe cand daca este utilizat ca un controler fuzzy, si viitorul dorit al raspunsului actual este comparat cu viitorul unor raspunsuri din baza de cunostinte.
Prezentul raspunsului se gaseste in baza de cunostinte si este desemnat prin celula selectata. Trecutul acestuia este alcatuit din sirul de celule gasite cu operatorii predecesor in timp, inclusiv celula selectata. Viitorul unui raspuns este alcatuit din sirul de celule gasite cu operatorii succesor in timp. Compararea inapoi in timp a doua raspunsuri se numeste evaluarea trecutului, pe cand compararea inainte in timp a doua raspunsuri se numeste evaluarea viitorului.
Adancimea evaluarii este data de numarul de momente de esantionare (celule) luate in calcul. Numarul maxim de momente de esantionare luate in calcul in trecut este np, iar in viitor nf. Adancimea evaluarii in trecut este foarte importanta. Daca latimea multimii fuzzy de comparare este suficient de mica si ordinul procesului este n, ordinul fuzzy np poate fi ales mai mic sau egal cu n. Evaluarea viitorului raspunsului actual nu este posibila, din cauza ca viitorul acesta fiind necunoscut. Totusi, este posibil sa se compare viitorul unui raspuns din baza de cunostinte cu viitorului raspunsului dorit, desemnat prin vectorul y+(k).
Daca
hp este adancimea
evaluarii, similaritatea dintre trecutul unui raspuns actual si
trecutul unui raspuns din baza de cunostinte poate fi
exprimata prin ![]() . Calculand urmatoarele diferente:
. Calculand urmatoarele diferente:
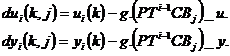 (5.20)
(5.20)
o masura a similaritatii are expresia:
![]() (5.21)
(5.21)
Gradul de asemanare al
celor doua raspunsuri este calculat ca fiind intersectia
valorilor de apartenenta la multimile fuzzy de comparatie a
diferentelelor in u si y, utilizand o valoare a lui g furnizata de catre
multimea fuzzy de liniarizare flin.
In mod similar se poate calcula ![]() , adica similaritatea intre trecuturile a doua
raspunsuri din baza de cunostinte.
, adica similaritatea intre trecuturile a doua
raspunsuri din baza de cunostinte.
Similaritatea
dintre viitorul dorit al raspunsului actual si viitorul
raspunsului din baza de cunostinte este exprimata prin ![]() Calculul ei porneste
de la determinarea diferentei:
Calculul ei porneste
de la determinarea diferentei:
![]() (5.22)
(5.22)
iar masura similaritatii este selectata in acord cu:
![]()
![]() (5.23)
(5.23)
Calculul celui mai bun factor de liniarizare se bazeaza pe comparatia intre valorile raspunsului actual si cele ale unor raspunsuri din baza de cunostinte
 ;
; 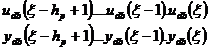 (5.24)
(5.24)
Cel mai bun g este acela care maximizeaza urmatoarea expresie:
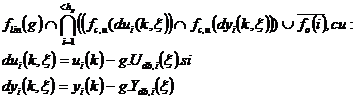 (5.25)
(5.25)
Calculul celui mai bun g consuma mult timp, deoarece operatia se face inaintea fiecarei comparatii, adica de mai multe ori la fiecare moment de esantionare. Rezultatele experimentale indica a fi suficienta si o expresie mai simpla a lui g, valabila pentru np perioade de esantionare, care se obtine prin maximizarea expresiei:
![]() (5.26)
(5.26)
Operatorul fuzzy de intersectie este de obicei cel minimal sau de tip produs. Ca rezultat al unor calcule simple, atunci cand se utilizeaza operatorul minimal, obtinem formula:
![]() (5.27)
(5.27)
Daca multimile fuzzy de comparare pentru u si y nu sunt identic alese, formula 5.27 poate da insa pentru g o valoare nesatisfacatoare.
In sistemele fuzzy intrarea si iesirea sunt limitate - in general experimental - prin valorile specifice procesului u-, u+, y-, y+. Daca limitele procesului liniar se aleg astfel incat linia care uneste punctele (u-, y-), (u+, y+) - numita dreapta de liniarizare - trece prin origine, ele se numesc proportionale. In caz contrar, limitele sunt neproportionale. In primul caz, factorul de liniarizare poate fi aplicat prin multiplicare. In algoritmi, pentru simplitate, vom presupune totdeauna ca limitele sunt proportionale.
|
Politica de confidentialitate |
| Copyright ©
2025 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |