
Proprietatile magnetice ale unui supraconductor
Se considera un material
delimitat de o suprafata S impenetrabila pentru sarcini
electrice. Notand ![]() densitatea de curent
in interiorul materialului si
densitatea de curent
in interiorul materialului si ![]() densitatea de curent
in exteriorul materialului, ecuatia Maxwell - Ampère se scrie:
densitatea de curent
in exteriorul materialului, ecuatia Maxwell - Ampère se scrie:

In regim lent variabil termenul de deplasare este neglijabil, deci, pentru orice punct din interiorul materialului se poate scrie:
 (6)
(6)
Deci, intr-un material
supraconductor densitatea de curent este nula. Curentii
supraconductori nu pot sa circule decat la suprafata
supraconductorului. Densitatea acestora, ![]() , se obtine pornind de la discontinuitatea lui
, se obtine pornind de la discontinuitatea lui ![]() la traversarea
suprafetei S. Se obtine
la traversarea
suprafetei S. Se obtine
 (7)
(7)
Este de remarcat faptul ca in
aceasta valoare de ![]() nu intervine nici o
caracteristica a mediului considerat. Valoarea sa este limitata de
nu intervine nici o
caracteristica a mediului considerat. Valoarea sa este limitata de ![]() care trebuie sa
fie suficient de mic pentru ca
care trebuie sa
fie suficient de mic pentru ca ![]() sa fie, in
apropierea suprafetei, mai mic decat campul critic
sa fie, in
apropierea suprafetei, mai mic decat campul critic ![]() pentru ca materialul
sa ramana supraconductor.
pentru ca materialul
sa ramana supraconductor.
Momentul magnetic ![]() al unui volum V din
material, parcurs de curenti superficiali, are expresia:
al unui volum V din
material, parcurs de curenti superficiali, are expresia:
![]()
Magnetizatia este legata de densitatea de curent prin relatia:
![]()
iar momentul magnetic se scrie:
![]() (8)
(8)
Deci materialul supraconductor
plasat in campul magnetic extern ![]() are un moment magnetic
global
are un moment magnetic
global ![]() .
.
Tinand seama ca relatia
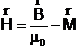
devine
![]() (9)
(9)
se
constata ca pentru un supraconductor ![]() sunt opusi, ceea
ce conduce la o valoare infinita pentru susceptibilitatea magnetica
sunt opusi, ceea
ce conduce la o valoare infinita pentru susceptibilitatea magnetica  si o valoare
nula pentru permeabilitatea magnetica
si o valoare
nula pentru permeabilitatea magnetica ![]() . Lucrurile se petrec ca si cum materialul
supraconductor ar fi un diamagnetic perfect.
. Lucrurile se petrec ca si cum materialul
supraconductor ar fi un diamagnetic perfect.
O manifestare spectaculoasa a comportamentului diamagnetic perfect a unui supraconductor este levitatia unui magnet deasupra suprafetei unui supraconductor.
Acest fenomen poate fi interpretat
utilizand expulzarea campului magnetic in exteriorul materialului
supraconductor. Curentii suraconductori care apar pentru a anula ![]() creaza in
exterior un camp magnetic
creaza in
exterior un camp magnetic ![]() . Magnetul, de moment magnetic
. Magnetul, de moment magnetic ![]() , presupus rigid, este supus unei forte:
, presupus rigid, este supus unei forte:
![]() (10)
(10)
Presupunand ![]() orientat dupa
verticala ascendent, si stiind ca
orientat dupa
verticala ascendent, si stiind ca ![]() este de sens opus,
relatia (10) conduce la:
este de sens opus,
relatia (10) conduce la:
![]()
Echilibrul magnetului se
realizeaza atunci cand greutatea sa, ![]() , este compensata de forta din relatia (10),
deci
, este compensata de forta din relatia (10),
deci
 (11)
(11)
|
Politica de confidentialitate |
| Copyright ©
2026 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |