
Raportarea secundarului la primar - schema echivalenta
La transformatoarele
reale, obisnuit numarul de spire al infasurarii
primare w1 este diferit
de numarul de spire al infasurarii secundare w2. Din acest motiv, t.e.m.
induse in cele doua infasurari sunt diferite ca
marime, curentii ce trec prin acestea sunt diferiti,
rezistentele si reactantele de asemenea se deosebesc. Aceasta
ingreuneaza compararea cantitativa a marimilor celor doua
infasurari. Iata de ce, in studiile teoretice obisnuit
se raporteaza marimile infasurarii secundare la cele
ale infasurarii primare. Astfel, transformatorul real cu numere
diferite de spire (w1![]() w2) se
inlocuieste cu un transformator echivalent cu acelasi numar de
spire la cele doua infasurari. Acest transformator este
numit raportat, la care se admite ca infasurarea
secundara a transformatorului real este inlocuita cu una fictiva
ce are
w2) se
inlocuieste cu un transformator echivalent cu acelasi numar de
spire la cele doua infasurari. Acest transformator este
numit raportat, la care se admite ca infasurarea
secundara a transformatorului real este inlocuita cu una fictiva
ce are ![]() spire.
spire.
Astfel, valorile reale
ale marimilor secundare se substituie cu valorile lor strict determinate
ce corespund marimilor raportate, marimile primare ramanand
neschimbate. Se admite ca marimile raportate se noteaza cu
indicele prim "![]() ".
".
In infasurarea secundara a
transformatorului real cu w2
spire se induce t.e.m. ![]() , iar in infasurarea secundara a
transformatorului raportat cu
, iar in infasurarea secundara a
transformatorului raportat cu ![]() spire se induce t.e.m.:
spire se induce t.e.m.:
![]() . Efectuand raportul
. Efectuand raportul ![]() si explicitand t.e.m.
si explicitand t.e.m. ![]() se obtine:
se obtine:

deoarece  - raportul de transformare
- raportul de transformare
T.e.m. ![]() este numita
t.e.m. secundara raportata. Deoarece la transforma-torul raportat
t.e.m. indusa in infasurarea secundara este egala cu
aceea din infasu-rarea primara (
este numita
t.e.m. secundara raportata. Deoarece la transforma-torul raportat
t.e.m. indusa in infasurarea secundara este egala cu
aceea din infasu-rarea primara (![]() =E1), raportul
de transformare este egal cu unitatea.
=E1), raportul
de transformare este egal cu unitatea.
Pentru ca infasurarea secundara fictiva sa fie echivalenta cu cea reala, este necesar ca t.m.m. a celor doua infasurari sa fie una si aceeasi, adica solenatiile create de cele doua infasurari, trebuie sa fie egale:
![]() (2.26)
(2.26)
Din egalitatea (2.26) se determina valoarea curentului secundar raportat:
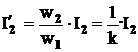
Expresia marimii curentului secundar raportat coincide cu expresia celei de-a doua componente a curentului primar al transformatorului in regim de sarcina.
Pentru echivalare, este necesar ca pierderile prin efect Joule in infasurarile secundare fictiva si reala sa fie aceleasi, adica:
![]() (2.27)
(2.27)
Din egalitatea (2.27) se determina valoarea rezistentei active raportate a infasurarii secundare:

La raportarea marimilor infasurarii secundare la primar este necesar a se pastra raportul dintre rezistentele si reactantele secundare ale transformatoarelor real si raportat, adica a se mentine egalitatea pierderilor active si reactive de putere pentru cele doua situatii:
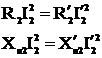
incat prin raportare rezulta:
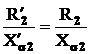 (2.28)
(2.28)
Din relatia (2.28) se determina marimea reactantei de dispersie raportata:
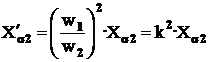
Analog se raporteaza si marimile sarcinii cuplate la iesirile infasurarii secundare a transformatorului. In fig.2.12 se prezinta diagrama fazoriala a transfor-matorului raportat cu sarcina inductiva. Ea se construieste analog cu aceea a transformatorului real pe baza ecuatiilor transformatorului raportat ce au urmatoa-rea forma:
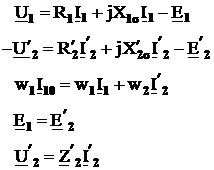 (2.29)
(2.29)
Pentru simplitatea diagramei nu sunt
reprezentate fluxurile de dispersie ![]() si
si ![]() si t.e.m. induse
de acestea. Diagrama fazoriala a transformatorului raportat se
deosebeste de a celui real numai prin aceea ca
si t.e.m. induse
de acestea. Diagrama fazoriala a transformatorului raportat se
deosebeste de a celui real numai prin aceea ca ![]() =E1.
Aceasta permite alege-rea de scari identice pentru marimile celor doua
infasurari, care usureaza compa-rarea lor.
=E1.
Aceasta permite alege-rea de scari identice pentru marimile celor doua
infasurari, care usureaza compa-rarea lor.

Fig.2.12 Diagrama fazoriala a transformatorului
raportat cu sarcina inductiva
In fig.2.13 se prezinta schemele
echivalente ale infasurarilor primara si
se-cundara ale transformatorului raportat. Cele doua
infasurari sunt cuplate inductiv prin fluxul ![]() . Raportarea marimilor infasurarii
secundare la primar, adica substi-tutia echivalenta a
transformatorului real cu cel echivalent, a permis ca aceasta legatura
inductiva dintre infasurari sa fie inlocuita cu
legatura electrica (galvanica) si a se stabili schema
echivalenta a transformatorului.
. Raportarea marimilor infasurarii
secundare la primar, adica substi-tutia echivalenta a
transformatorului real cu cel echivalent, a permis ca aceasta legatura
inductiva dintre infasurari sa fie inlocuita cu
legatura electrica (galvanica) si a se stabili schema
echivalenta a transformatorului.

Fig.2.13 Schemele echivalente ale infasurarilor
primara respectiv secundara ale transformatorului raportat
Deoarece, cele
doua infasurari ale transformatorului sunt izolate una
fata de alta, regimul fiecareia dintre ele nu se schimba,
daca se unesc electric doua puncte ale lor, ex. punctele 2 si 4.
Prin aceasta se egalizeaza numai potentialele acestor puncte.
Totodata, din egalitatea ![]() =E1
rezulta ca, in fiecare moment punctele 1 si 3 au potentiale
identice, care permit ca si ele sa fie conectate electric. Simultan
cu aceasta partile celor doua infasurari dintre
punctele 1, 2 si dintre punctele 3, 4 se pot uni intr-o portiune
comuna celor doua circuite. Potrivit acestui procedeu lega-tura
inductiva dintre infasurari se substituie cu cea
electrica, obtinandu-se astfel schema echivalenta in T a
transformatorului (fig.2.14).
=E1
rezulta ca, in fiecare moment punctele 1 si 3 au potentiale
identice, care permit ca si ele sa fie conectate electric. Simultan
cu aceasta partile celor doua infasurari dintre
punctele 1, 2 si dintre punctele 3, 4 se pot uni intr-o portiune
comuna celor doua circuite. Potrivit acestui procedeu lega-tura
inductiva dintre infasurari se substituie cu cea
electrica, obtinandu-se astfel schema echivalenta in T a
transformatorului (fig.2.14).

Fig.2.14 Schema echivalenta in T a transformatorului
Aceasta
schema trebuie sa indeplineasca toate ecuatiile pentru
t.e.m. si cu-rentii transformatorului. Deoarece ![]() , din prima lege a lui Kirchhoff se observa, ca
prin portiunea comuna celor doua circuite trece curentul de
functio-nare in gol I10.
In regimul de functionare in gol, transformatorul consuma:
, din prima lege a lui Kirchhoff se observa, ca
prin portiunea comuna celor doua circuite trece curentul de
functio-nare in gol I10.
In regimul de functionare in gol, transformatorul consuma:
puterea activa P10, pentru acoperirea pierderilor datorate curentilor turbionari si fenomenului histerezis din miezul magnetic;
puterea reactiva Q10 pentru crearea fluxului
magnetic ![]() .
.
Iata de ce latura circuitului, prin care
trece curentul I10,
trebuie sa contina rezistenta activa ![]() si reactanta
si reactanta![]() , in care se consuma corespunzator puterile
activa si reactiva, egale cu acelea consumate de transformator
la functionarea in gol. Impedanta complexa a laturii de
magnetizare este
, in care se consuma corespunzator puterile
activa si reactiva, egale cu acelea consumate de transformator
la functionarea in gol. Impedanta complexa a laturii de
magnetizare este ![]() , si trebuie a se indeplini conditia
, si trebuie a se indeplini conditia 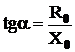 , unde
, unde ![]() este unghiul de
defazaj dintre curentul I10
si fluxul
este unghiul de
defazaj dintre curentul I10
si fluxul ![]() .
.
Potrivit acestui procedeu, schema echivalenta a transformatorului (fig.2.14) contine trei laturi:
primara cu impedanta
proprie ![]() parcursa de
curentul I1;
parcursa de
curentul I1;
de magnetizare cu impedenta ![]() strabatuta de curentul I10;
strabatuta de curentul I10;
secundara cu doua
impedante: proprie ![]() si de
sarcina
si de
sarcina ![]() parcurse de curentul
parcurse de curentul![]() .
.
Semnul minus din fata curentului secundar raportat inseamna ca t.m.m. a infasurarii secundare a transformatorului este opusa t.m.m. a infasurarii primare.
Toti parametrii schemei echivalente cu exceptia
lui ![]() sunt constanti
pentru transformatorul dat si dupa cum se va vedea din cele
urmatoare, ei se pot determina din incercarile de functionare in
gol si la scurtcircuit. Schema echivalenta ofera posibilitatea
de studiu a transformatorului in toate regimurile de functionare. Pentru
diferite valori ale lui
sunt constanti
pentru transformatorul dat si dupa cum se va vedea din cele
urmatoare, ei se pot determina din incercarile de functionare in
gol si la scurtcircuit. Schema echivalenta ofera posibilitatea
de studiu a transformatorului in toate regimurile de functionare. Pentru
diferite valori ale lui ![]() se determina toti curentii, tensiunile si
diferentele de faza, cand aceasta determinare se reduce la
studiul circuitului de c.a. Spre exemplu, la
se determina toti curentii, tensiunile si
diferentele de faza, cand aceasta determinare se reduce la
studiul circuitului de c.a. Spre exemplu, la ![]() , curentul
, curentul ![]() si
si ![]() , aceasta inseamna ca se obtine posibilitatea
de studiu a transformatorului la functionarea in gol. Pentru
, aceasta inseamna ca se obtine posibilitatea
de studiu a transformatorului la functionarea in gol. Pentru ![]() se obtine
se obtine ![]() , adica se poate studia transformatorul in regim de
scurtcircuit. Potrivit acestui procedeu, la variatia sarcinii
, adica se poate studia transformatorul in regim de
scurtcircuit. Potrivit acestui procedeu, la variatia sarcinii ![]() de la zero la infinit
este posibil studiul transformatorului in toate regimurile lui de
functionare.
de la zero la infinit
este posibil studiul transformatorului in toate regimurile lui de
functionare.
Schema echivalenta permite stabilirea modelului transformatorului, iar studiul modelului este identic cu studiul transformatorului real. Pe baza schemei echivalente se poate construi diagrama fazoriala. In fig.2.15 este prezentata diagra-ma fazoriala a schemei echivalente pentru sarcina cu caracter inductiv.
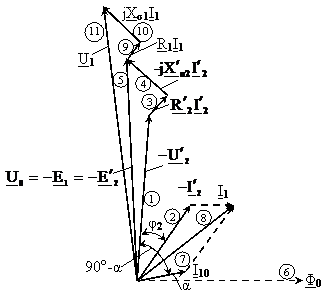
Fig.2.15 Diagrama fazoriala a transformatorului
pentru sarcina cu caracter inductiv.
Constructia ei incepe de la fazorii
tensiunii secundare raportate ![]() si cu-rentului
secundar raportat
si cu-rentului
secundar raportat ![]() , intre care exista defazajul
, intre care exista defazajul 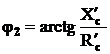 .
.
In continuare, se adauga fazorului
tensiunii![]() , fazorii caderilor de tensiu-ne activa
, fazorii caderilor de tensiu-ne activa ![]() si reactiva
si reactiva ![]() , rezultand fazorul tensiunii
, rezultand fazorul tensiunii ![]() . Cu unghiul (90°-
. Cu unghiul (90°-![]() ) in urma fata de fazorul tensiunii
) in urma fata de fazorul tensiunii ![]() se con-struieste
fazorul curentului
se con-struieste
fazorul curentului ![]() . Suma fazorilor curentilor
. Suma fazorilor curentilor ![]() si
si ![]() determina
curentul
determina
curentul ![]() . Sensul obtinut pentru fazorul
. Sensul obtinut pentru fazorul ![]() determina in
continuare sensurile fazorilor caderilor de tensiune
determina in
continuare sensurile fazorilor caderilor de tensiune ![]() si
si ![]() , care insumati cu fazorul tensiunii
, care insumati cu fazorul tensiunii ![]() , stabileste marimea si sensul fazorului
tensiunii primare
, stabileste marimea si sensul fazorului
tensiunii primare ![]() .
.
Daca se are in vedere ca, curentul ![]() este (3÷10)% din
curentul nominal primar I1n
al transformatorului, in studiul regimurilor de sarcina se admite ca
este (3÷10)% din
curentul nominal primar I1n
al transformatorului, in studiul regimurilor de sarcina se admite ca ![]() . Astfel,
. Astfel, ![]() , ceea ce permite simplificarea schemei echivalente a
transformatorului daca se inlatura circuitul de magnetizare cu
parametrii R0 si X0, rezultand schema
echivalenta simplificata (Kapp) indicata in fig.2.16, unde
, ceea ce permite simplificarea schemei echivalente a
transformatorului daca se inlatura circuitul de magnetizare cu
parametrii R0 si X0, rezultand schema
echivalenta simplificata (Kapp) indicata in fig.2.16, unde ![]() si
si ![]() . In consecinta, transformatorul poate fi examinat
ca o impedanta
. In consecinta, transformatorul poate fi examinat
ca o impedanta ![]() , determinata de rezistentele si de
reactantele inductive ale infasurarilor prin care trece
curentul
, determinata de rezistentele si de
reactantele inductive ale infasurarilor prin care trece
curentul![]() . In fig.2.17 se prezinta diagrama fazoriala pentru
schema echivalenta simplificata (Kapp).
. In fig.2.17 se prezinta diagrama fazoriala pentru
schema echivalenta simplificata (Kapp).
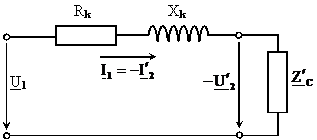
Fig.2.16 Schema echivalenta simplificata a transformatorului
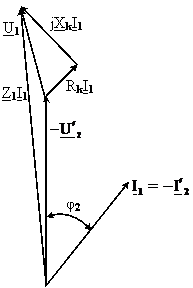
Fig.2.17 Diagrama fazoriala corespunzatoare schemei
echivalente simplificate a transformatorului
|
Politica de confidentialitate |
| Copyright ©
2025 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |