
Reprezentarea matematica generala a ansamblului instalatiilor primare ale unei centrale electrice
1. Modelul instalatiilor primare ale centralei termoelectrice
Pe baza modelelor matematice ale elementelor componente ale unei centrale termoelectrice descrise in paragrafele anterioare se poate concepe o schema functionala de ansamblu pentru partea termomecanica a unei centrale electrice, schema care pe langa faptul ca descrie matematic functionarea sistemului fizic corespunzator, permite determinarea tuturor legaturilor dintre diferitele blocuri functionale si scrierea intregului set de ecuatii ce caracterizeaza comportarea dinamica a acestui ansamblu. Schema functionala a ansamblului instalatiilor termomecanice fara sistem coordonator centralizat este reprezentata in figura 2.28.
![]() Modelul reprezentat in figura 2.28
permite modelarea atat a instalatiilor primare prevazute cu cazane cu
tambur, cat si a celor cu cazane cu strabatere fortata,
considerarea influentei debitului de abur de la turbina, , in sistemele de reglare ale cazanului
si al SRAV si luarea in considerare a pierderilor din conductele de
abur.
Modelul reprezentat in figura 2.28
permite modelarea atat a instalatiilor primare prevazute cu cazane cu
tambur, cat si a celor cu cazane cu strabatere fortata,
considerarea influentei debitului de abur de la turbina, , in sistemele de reglare ale cazanului
si al SRAV si luarea in considerare a pierderilor din conductele de
abur.
Functionarea ansamblului este descrisa de un set de 24 de ecuatii algebrice si diferentiale la care se adauga inecuatiile limitarilor corespunzatoare, dupa cum urmeaza:


Fig.2.28 Schema bloc de functionare a instalatiilor primare ale unei centrale termoelectrice.
Valorile variabilelor pentru regimul stationar initial, anterior perturbatiei se obtin anuland derivatele din sistemul de ecuatii (2.73) si cunoscand ca in regim stationar: ωc = ωo; Spc = Pmo; P = P0; ptc = ptn si Sp10 = 0.
Relatiile (2.73) caracterizeaza complet functionarea instalatiilor primare termomecanice si pot fi particularizate pentru diverse tipuri constructive ale acestora prin valori corespunzatoare date coeficientilor K, Kf, KPT, si KPD. Prin aceasta, ele pot fi utilizate corespunzator pentru modelarea diferitelor tipuri de centrale termoelectrice dintr-un sistem electroenergetic analizat.

2. Modelul instalatiilor primare ale centralei hidroelectrice
Schema de functionare pentru instalatiile primare ale unei centrale hidroelectrice a fost prezentata in figura 2.22, iar ecuatiile corespunzatoare modelului matematic sunt relatiile (2.66). Daca la aceasta schema de functionare se mai adauga reprezentarea generala a SRAV si blocul corespunzator inertiei mecanice a ansamblului rotoarelor turbinei-generator sincron, rezulta schema de functionare generala din figura 2.29.
Ecuatiile care descriu complet functionarea instalatiilor primare ale centralei hidroelectrice sunt formate din sistemul de ecuatii (2.66) al cresterilor variabilelor hidromecanice, cresteri care se adauga la fiecare pas de calcul, la valorile marimilor din regimul stationar anteperturbatie si din sistemul de ecuatii (2.71) ale SRAV care se completeaza cu ecuatia de miscare a rotoarelor turbina -generator sincron.
Regimul stationar anteperturbatie se obtine cu ecuatiile (2.67) si conditiile initiale descrise la reprezentarea SRAV.

Fig.2.29. Schema bloc de functionare a instalatiilor primare ale unei centrale hidroelectrice.
Pentru simularea proceselor dinamice din centrale, utilizand modelele matematice ale instalatiilor primare termo si hidromecanice, s-au conceput doua programe de calcul, TERMO si HIDRO, scrise in limbaj FORTRAN IV pentru calculatorul Felix C 512, a caror scheme logice sunt descrise in figura 2.30 a si b.
Programele au avut drept scop studierea modului in care sistemele de ecuatii corespunzatoare celor doua modele matematice satisfac conditiile initiale corespunzatoare unui regim stationar anteperturbatie si ale calculului valorilor initiale ale variabilelor, modul in care sistemele raspund la o perturbatie data, ajustarea valorilor constantelor modelelor matematice si in final, verificarea stabilitatii modelelor in vederea cuplarii lor la modelele matematice ale generatorului sincron, retelei si consumatorilor.
Integrarea ecuatiilor diferentiale din cadrul celor doua modele s-a facut printr-o metoda Runge-Kutta de ordinul IV.

Fig.2.30. Ordinogramele de principiu ale programelor de calcul pentru modelarea instalatiilor primare.
a) Programul TERMO;
b) Programul HIDRO.
3. Interpretarea rezultatelor simularii pe calculatorul numeric
a instalatiilor primare
Cu ajutorul programului TERMO s-a analizat raspunsul in timp al unei instalatii primare termomecanice prevazuta cu un generator de abur cu tambur, precum si a unei instalatii echipata cu cazan cu strabatere fortata, la o crestere brusca a sarcinii electrice cu 10% la barele generatorului sincron. S-a considerat un generator de abur avand presiunea nominala a aburului de pt0 = 140 at. si un debit nominal de abur, mCV0 = 630 t/h, alimentand cu abur un grup energetic turbina-generator sincron cu puterea mecanica nominala, Pmn = 210 MW si timpul de lansare, TL = 6,5 s la Hz.
Constanta de timp de inertie a cazanului a fost, PP =300 s, iar principalele constante ale automatizarilor cazanului pe calea combustibil-aer, au fost KP = 3,3 ; KI = 0,022 ; TR = 24 s; Kf = 0 (cazan coordonator), TC = 25 s; TF = 30 s, iar a caii apei de alimentare: Kw1 = 1,5; Kw2 = 0,5; M = 5 s. Turbina, in 3 trepte cu supraincalzire intermediara a avut parametri: TCM = 0,5 s, TRH=7s; TC0 = 0,4 s; FHP = 0,3; FIP = 0,4 ; FLP = 0,3. Analiza evolutiei dinamice a sistemului termomecanic s-a facut initial pentru un timp de 50 sec. cu un pas de incrementare a timpului Dt = 0,5 sec., iar apoi, pentru ca perioada de timp de analiza a fost prea mica si nu conducea la concluzii clare s-a marit timpul de analiza la 100 s cu un pas de incrementare de Dt = 1 s.
Toate marimile s-au scris in u.r.n. Rezultatele analizei sunt reprezentate in figurile 2.31, 2.32, 2.33, 2.34. Curbele s-au trasat cu calculatorul, pentru fiecare marime reprezentata adoptandu-se scara corespunzatoare extinderii sale maxime. Analizand curbele obtinute se constata ca la cresterea brusca a necesarului de putere in SEE, incepe deschiderea supapelor de admisie a aburului (curba Spt). Se mareste astfel debitul de abur la turbina (curba mHP), iar puterea mecanica incepe sa creasca (curba Pm).
Presiunea aburului scade (curba pt) datorita cresterii debitului acestuia la turbina si inertiei mari a instalatiei primare de alimentare cu combustibil. Frecventa (curba w) scade deoarece puterea electrica de franare este mai mare decat puterea mecanica. Se observa ca atat in cazul cazanului cu tambur, cat si a celui cu strabatere fortata, dupa parcurgerea unui interval de timp de 50 secunde nu se pot trage concluzii clare privind stabilitatea sistemului termomecanic (figurile 2.31 si 2.32). De aceea s-a impus extinderea scalei timpului de analiza. Pentru un interval de timp de 100 secunde se vede ca in cazul cazanului cu tambur (figura2.33) are loc pierderea stabilitatii sistemului termomecanic, dupa aproximativ 60 de secunde de la perturbatie. Acest lucru se datoreste inertiei mari a caii combustibil-aer care nu incarca suficient de rapid cazanul, fapt ce conduce la continua scadere a presiunii aburului.
Supapele de admisie se deschid la maximum, dar nu se mai poate asigura debitul de abur necesar cresterii puterii mecanice pentru echilibrarea deficitului de putere la barele G.S. Pierderea stabilitatii instalatiei termomecanice va conduce implicit la pierderea sincronismului G.S. dupa 60 secunde de la aparitia primei perturbatii, fapt ce va constitui o noua perturbatie in SEE. In cazul cazanului cu strabatere fortata, analizand comportarea dinamica pe 50 secunde (figura 2.32) s-ar putea trage concluzia ca sistemul termomecanic tinde sa-si piarda stabilitatea. Totusi, faptul ca dupa aproximativ 32 de secunde, datorita rapiditatii caii dinamice a apei de alimentare, presiunea aburului dat de cazan incepe sa creasca, iar aportul suficient de abur conduce la o tendinta de inchidere a supapelor de admisie la turbina, indeamna la continuarea analizei dinamicii pentru o scala de timp mai mare. Extinzand scala de timp la 100 de secunde se remarca tendinta de stabilizare (figura 2.34) a functionarii sistemului termomecanic printr-un proces oscilatoriu amortizat al tuturor marimilor termice si mecanice.
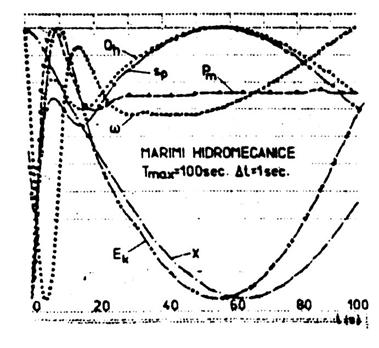
Pentru stimularea comportarii dinamice a unei centrale hidroelectrice s-a considerat un grup hidroenergetic echipat cu o turbina Francis cu puterea de, Pmn = 67,2 MW la f = 50 Hz, avand turatia nominala n0 = 39,3 rad/s, raza de referinta, R = 0,86 m si timpul de lansare al grupului, M = 7,5 s. Pentru cifra de viteza nominala, v0 = 0,408 obtinuta la debitul nominal de, Qh = 127 m2/s s-au obtinut parametri unghiulari ai turbinei, la functionare in regim nominal, t1 = 0,47; t2 = 0,6; t3 = - 0,03 ; t4 = -0,23. Amenajarea hidraulica s-a considerat formata dintr-o conducta de aductiune cu lungimea, Lg = 750 m si sectiunea Sg = 23 m2, un castel de echilibru cu sectiunea de Sch = 200 m2 si o conducta fortata lunga de Lc = 172 m si cu sectiunea de Sc = 31,2 m2. Caderea bruta a amenajarii a fost Hb0 = 66,32 m, caderea in conducta de aductiune de Hg0 = 3,5m, rezultand o cadere neta de Hk0 = 61,97m. Viteza apei in conducta de aductiune, in regim nominal s-a considerat vg0 = 5,52 m/s si in conducta fortata, vc0 = 4,07 m/s. Pentru cele trei elemente ale amenajarii hidraulice s-au considerat urmatoarele constante de timp de inertie Tgi = 6,7 s; Tch = 99 s; si Tc = 1,15 s. Comportarea dinamica a instalatiei hidromecanice s-a analizat pentru o perturbatie in SEE constand din cresterea puterii electrice la barele G.S. cu 10 % fata de regimul stationar. S-a urmarit evolutia in timp a marimilor mecanice si hidraulice pe un interval de 50 de secunde (figura 2.35) si, deoarece rezultatele nu erau concludente, s-a extins scala timpului de analiza pe un interval de 100 de secunde (figura 2.36) cu pasul de incrementare a timpului, Dt = 1 s.
Se observa, din ambele figuri, ca la cresterea brusca a puterii electrice ceruta la barele G.S., frecventa scade rapid datorita aparitiei unui cuplu puternic de franare. Sistemul de reglare a vitezei sesizeaza scaderea frecventei (curba w) si comanda deschiderea vanelor de admisie a apei (curba Sp). Vanele de admisie se deschid la inceput foarte rapid, iar puterea mecanica creste, depasind valoarea puterii electrice (curba Pm), fapt ce conduce la aparitia unui cuplu de accelerare si frecventa creste.
Odata cu deschiderea vanelor are loc insa, o crestere a debitului de apa vehiculat prin turbina (curba Qh), care nu poate fi compensat de apa ce se scurge din baraj, prin conducta de aductiune si nivelul apei in castelul de echilibru incepe sa scada (curba X) ducand la micsorarea caderii nete, (presiunii la turbina) si corespunzator, la reducerea energiei specifice nete (curba Ek).
Acest proces dinamic din amenajarea hidraulica, datorita inertiei mari a acesteia, se produce mult mai lent decat procesul dinamic de reglare dat de SRAV, care acum sesizand cresterea frecventei comanda inchiderea vanelor si reduce puterea mecanica sub valoarea puterii electrice. Frecventa scade si reincepe deschiderea vanelor, dar cum nivelul apei in castelul de echilibrare este mai redus si caderea neta este mai mica, pentru obtinerea unei puteri mecanice corespunzatoare este nevoie de un debit mai mare de apa si pe un interval mai are de timp. Dupa echilibrarea bilantului de puteri se comanda inchiderea vanelor, fapt ce conduce la cresterea nivelului apei in castelul de echilibru si a energiei specifice nete, corespunzatoare.
Rezultatele obtinute in simularea comportarii dinamice a instalatiilor termo si hidromecanice ale centralelor electrice pe o perioada de 100 de secunde au impus extinderea timpului de simulare pentru o mai buna apreciere a desfasurarii fenomenelor lente legate de frecventa si debitul si presiunea aburului, respectiv de debitul, energia specifica neta si nivelul apei in castelul de echilibru. In figurile 2.37 si 2.38 sunt reprezentate curbele de oscilatie in timp ale principalelor marimi termo respectiv hidromecanice ale instalatiilor primare considerate pentru un test de comportare dinamica extins pe 200 secunde. S-a mentinut aceeasi perturbatie initiala si anume cresterea cu 10 % a puterii ceruta la barele centralelor. Urmarind curbele de oscilatii in timp din figurile 2.37 si 2.38 se constata, dincolo de domeniul cunoscut de 100 de secunde, tendinta evidenta de "linistire" a proceselor dinamice, alaturi de oscilatiile lente si usor amortizate ale frecventei.



|
Politica de confidentialitate |
| Copyright ©
2026 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |