Rezonanta paralel
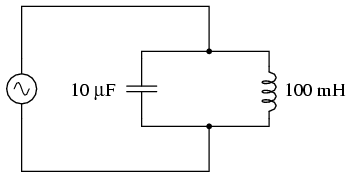
Putem ajunge la o stare de rezonanta intr-un circuit oscilator (LC), daca reactantele condensatorului si a bobinei sunt egale intre ele. Deoarece reactanta inductiva creste odata cu cresterea frecventei, iar reactanta capacitiva scade cu cresterea frecventei, exista doar o singura frecventa unde cele doua reactante vor fi egale.
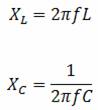
Din egalitatea celor doua ecuatii de mai sus, obtinem:
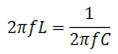
Inmultim ambele ecuatii cu f
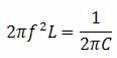
Impartim ambele ecuatii cu 2πf
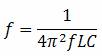
Rezolvand si simplificand ecuatia de mai sus, obtinem urmatorul rezultat:
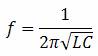
In circuitul de mai sus, avem un condensator de 10 µF si o bobina de 100 mH. Din moment ce cunoastem ecuatiile pentru determinarea reactantelor, oricare ar fi valoarea frecventei, iar ceea ce ne intereseaza este punctul in care cele doua reactante sunt egale intre ele, putem rezolva ecuatia formata din egalitatea celor doua reactante pentru a afla frecventa de rezonanta (naturala).
Aceasta este formula prin care putem afla frecventa de rezonanta a unui circuit oscilator, atunci cand cunoastem valorile inductantei (L) si a capacitatii (C). Dupa introducerea valorilor L si C in formula de mai sus, ajungem la frecventa de rezonanta de 159,155 Hz.
Ceea ce se intampla la rezonanta este interesant. Fiindca reactanta inductiva este egala cu cea capacitiva, impedanta totala creste spre infinit, ceea ce inseamna ca circuitul oscilator nu "consuma" deloc curent de la sursa de tensiune! Putem calcula impedantele individuale ale condensatorului de 10 µF si a bobinei de 100 mH.
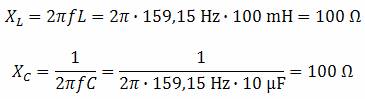
Prin urmare, ambele impedante sunt egale, 100 Ω. Putem apoi sa aplicam formula impedantei paralel pentru a demonstra matematic ceea ce am spus mai sus:
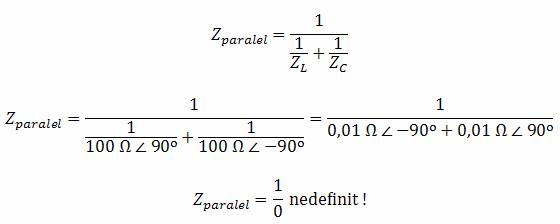
Desigur, nu putem face raportul unui numar cu zero pentru a ajunge la un rezultat care sa aiba sens, dar putem spune ca rezultatul tinde spre infinit pe masura ce valorile celor doua impedante paralel se apropie una de cealalta. Practic, acest lucru inseamna ca impedanta totala a circuitului oscilator la rezonanta este infinita (se comporta precum un circuit deschis).
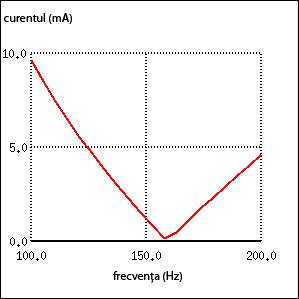
Grafic, amplitudinea curentului din circuit in functie de frecventa sursei de alimentare arata precum in figura alaturata. Punctul de pe grafic unde curentul este zero, coincide cu frecventa de rezonanta calculata mai sus, 159,155 Hz.
|
Politica de confidentialitate |
| Copyright ©
2026 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |