TRANZITII INDIRECTE
S-a aratat ca in cazul tranzitiilor banda-banda trebuie respectata regula conservarii impulsurilor. In unele cazuri se pot produce si tranzitii neverticale in care conservarea momentului este asigurata prin interventia unuia sau mai multor fononi; procesele multifononice au desigur o probabilitate mica. Astfel de tranzitie,numite indirecte, au loc de exemplu in
11
Ge, dand nastere
unor absorbtii apreciabile (desi mai mici decat cea directa); ele se fac intre
maximul de la ![]() al benzii de valenta si minimul benzii de conductie de la
marginea Brillouin , in directia
al benzii de valenta si minimul benzii de conductie de la
marginea Brillouin , in directia ![]() si determina largimea zonei interzise.
si determina largimea zonei interzise.
In cazul unei tranzitii indirecte , conditia conservarii momentului devine :
![]() , (45)
, (45)
unde ![]() este momentul fononului , iar
este momentul fononului , iar ![]() momentul fononului (neglijabil); semnul "minus" corespunde
absorbtiei unui fonon , iar semnul "plus" emisiei unui fonon. Conditia
conservarii energiei se poate pune sub forma :
momentul fononului (neglijabil); semnul "minus" corespunde
absorbtiei unui fonon , iar semnul "plus" emisiei unui fonon. Conditia
conservarii energiei se poate pune sub forma :
![]() , (46)
, (46)
unde ![]() este energia
fotonului. Se poate considera ca efectuarea unei tranzitii neverticale
este energia
fotonului. Se poate considera ca efectuarea unei tranzitii neverticale ![]() ,are loc in doua etape : mai intai are loc o tranzitie
verticala AI, apoi o ranzitie IB inauntrul benzii de conductie, energia din
starea I fiind mai mare decat energia din starea B:
,are loc in doua etape : mai intai are loc o tranzitie
verticala AI, apoi o ranzitie IB inauntrul benzii de conductie, energia din
starea I fiind mai mare decat energia din starea B:
![]() .
.
Starea I apare astfel permisa din punctual de vedere al conservarii mamentului , dar interzisa din punctual de vedere al conservarii energiei. Daca timpul petrecut de electroni in starea I este extreme de scurt, din relatia de incertitudine :
![]() , (47)
, (47)
rezulta ca imprecizia in determinarea energiei este foarte mare. Prin urmare , sunt posibile tranzitiile AI si IB, fiecare respectand conservarea momentului darn u si a energiei. Pentru tranzitia completa AB sunt inca satisfacute ambele conditii. Electronul mai poate executa tranzitia indirecta AB si astfel: mai intai in banda de valenta, intre starile AI', prin absorbtia sau emisia unui fonon , apoi din starea intermediara I'in B printr-o tranzitie verticala.
Posibilitatea existentei starilor
virtuale I si I' , reiese din teoria perturbatiilor impinsa la al doilea ordin
de aproximatie. Spre deosebire de tranzitiile directe, unde starile initiala si
finala sunt fixate si limitate prin cele doua reguli de conservare (a
impulsului si a energiei) , la tranzitiile indirecte, stari initiale pot fi
toate starile din banda de valenta, cu energii (masurate de la maximul benzii
de valenta in jos) cuprinse intre zero si ![]() . Stari finale pot fi toate starile din banda de conductie cu
energii cuprinse intre
. Stari finale pot fi toate starile din banda de conductie cu
energii cuprinse intre ![]() si zero. Cand
si zero. Cand ![]() este mic,
este mic, ![]() poate fi
poate fi
12
considerat constant.
Pentru calcularea probabilitatii de
tranzitie a unui electron din starea cu functia de unda ![]() in starea cu functia de unda
in starea cu functia de unda ![]() sub actiunea unui foton si unui fonon, se considera
hamiltonianul de perturbare de forma :
sub actiunea unui foton si unui fonon, se considera
hamiltonianul de perturbare de forma :
![]() , (48)
, (48)
unde primul termen reprezinta
perturbarea datorita undei luminoase cu ![]() operator definit prin
operator definit prin ![]() ; al doilea termen reprezinta unda fononului , cu
; al doilea termen reprezinta unda fononului , cu ![]() vector constant definit prin
vector constant definit prin ![]() , ecuatia modului de vibratie al retelei cu frecventa
, ecuatia modului de vibratie al retelei cu frecventa ![]() , unde
, unde ![]() este deplasarea atomului cu vectorul de retea
este deplasarea atomului cu vectorul de retea ![]() din pozitia de echilibru.
din pozitia de echilibru.
Pornind de la starea A din banda de
valenta , electronul poate trece fie prin starea I' tot in banda de valenta ,
fie in starea I din banda de conductie. Se considera ![]() . In aproximatia de ordinal I al teoriei perturbatiilor ,
tranzitia nu este posibila; in aproximatia de ordinaul II se ajunge la
probabilitati de tranzitie proportionale cu timpul.
. In aproximatia de ordinal I al teoriei perturbatiilor ,
tranzitia nu este posibila; in aproximatia de ordinaul II se ajunge la
probabilitati de tranzitie proportionale cu timpul.
Se alege drept stare initiala una
din starile benzii de valenta cu functia de unda ![]() si vectorul de unda
si vectorul de unda ![]() apropiat de
apropiat de ![]() . Starea finala se
afla in banda de conductie , cu functia de unda
. Starea finala se
afla in banda de conductie , cu functia de unda ![]() si vectorul de unda
si vectorul de unda ![]() apropiat de
apropiat de ![]() corespunzator unui minim al benzii de conductie. Se pot forma
sase tipuri de matrice :
corespunzator unui minim al benzii de conductie. Se pot forma
sase tipuri de matrice :
![]() ,
, ![]() ;
;
![]() ,
, ![]() ;
;
![]() ,
, ![]() .
.
Dintre acestea , ![]() si
si ![]() sunt nule, deoarece momentul fotonului este neglijabil;
sunt nule, deoarece momentul fotonului este neglijabil; ![]() de asemenea se anuleaza deoarece nu exista tranzitii
banda-banda doar prin interactiune cu fononi, iar
de asemenea se anuleaza deoarece nu exista tranzitii
banda-banda doar prin interactiune cu fononi, iar ![]() este zero peste tot in afara de
este zero peste tot in afara de ![]() (tranzitii verticale).
Elementele de matrice care mai raman corespund tranzitiilor :
(tranzitii verticale).
Elementele de matrice care mai raman corespund tranzitiilor : ![]() , tranzitii directe din banda de valenta in banda de
conductie produse de un foton , iar
, tranzitii directe din banda de valenta in banda de
conductie produse de un foton , iar ![]() si
si ![]() tranzitiilor din banda
de conductie si banda de valenta produse de fotoni. Faptul ca
tranzitiilor din banda
de conductie si banda de valenta produse de fotoni. Faptul ca ![]() pentru toate valorile
pentru toate valorile
13
lui ![]() in afara de
in afara de ![]() , ne arata ca trebuie luate in considerare doar starile
inermediare
, ne arata ca trebuie luate in considerare doar starile
inermediare ![]() si
si ![]() care corespund
tranzitiilor verticale. Raman deci numai elementele de matrice :
care corespund
tranzitiilor verticale. Raman deci numai elementele de matrice : ![]() care se va nota cu
care se va nota cu ![]() si
si ![]() , care se va nota cu
, care se va nota cu ![]() .Avand doar doua stari inermediare este nevoie doar de doua
elemente de matrice de tipul
.Avand doar doua stari inermediare este nevoie doar de doua
elemente de matrice de tipul![]() si
si ![]() si anume :
si anume : ![]() si
si ![]() care se vor nota cu
care se vor nota cu ![]() si respectiv
si respectiv![]() . Pastrand doar termenii al caror numitor poate fi zero , din
calculul perturbatiilor in aproximatia a doua rezulta expresia coeficientului
. Pastrand doar termenii al caror numitor poate fi zero , din
calculul perturbatiilor in aproximatia a doua rezulta expresia coeficientului ![]() :
:
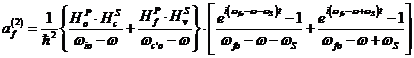 , (49)
, (49)
unde :
![]() ;
;
![]() ;
;
![]() .
.
Primii doi termini corespund tranzitiilor AB prin starea intermediara I, iar ultimii doi tranzitiilor AB prin starea intermediara I' cu absorbtia sau emisia unui fonon, dupa cum rezulta din conditia de anulare a numitorilor. Probabilitatile de tranzitie si deci coeficientul de absorbtie pot fi calculate separate pentru fiecare termen, apoi adunate pentru a obtine absorbtia totala.
Se incepe cu primul termen; pentru a
obtine probabilitatea de tranzitie trebuie sumat asupra tuturor valorilor
permise ale lui ![]() pastrand
pastrand ![]() fixat. Rezultatul se
inmulteste si cu numarul minimelor echivalente ale benzii de conductie M; se
obtine astfel:
fixat. Rezultatul se
inmulteste si cu numarul minimelor echivalente ale benzii de conductie M; se
obtine astfel:
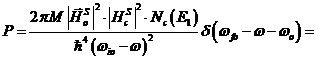
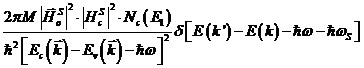 , (50)
, (50)
unde ![]() este o valoare medie,
iar
este o valoare medie,
iar ![]() .
.
Elementul de matrice ![]() este egal cu zero in afara de cazul cand
este egal cu zero in afara de cazul cand
14
![]() , (51)
, (51)
ceea ce determina
energia ![]() .Intr-o buna aproximatie se poate lua
.Intr-o buna aproximatie se poate lua![]() ; in aceste conditii
; in aceste conditii ![]() va fi gal cu
va fi gal cu ![]() , energia fononului corespunzatore lui
, energia fononului corespunzatore lui ![]() . Valorea lui
. Valorea lui ![]() este determinata
atunci prin functia
este determinata
atunci prin functia![]() din (50).
din (50).
![]() , (52)
, (52)
Expresia (52) exprima legea conservarii energiei in tranzitia cu absorbtie de fonon. Se introduc notatiile:
![]() ; (53)
; (53)
![]() . (54)
. (54)
Probabilitatea P, data de (50) este
diferita de zero cand ![]() este cuprins intre
zero si
este cuprins intre
zero si 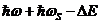 . Probabilitatea totala a acestui tip de tranzitii se obtine
sumand asupra tuturor valorilor lui
. Probabilitatea totala a acestui tip de tranzitii se obtine
sumand asupra tuturor valorilor lui![]() pentru care
pentru care ![]() . Factorii care depend slab de
. Factorii care depend slab de ![]() sunt scosi de sub
integrala, otinadu-se:
sunt scosi de sub
integrala, otinadu-se:
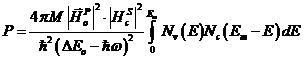 , (55)
, (55)
cu ![]() .
.
Pentru benzi parabolice, functiile ![]() si
si ![]() sunt proportionale cu
sunt proportionale cu ![]() . Inlocuind si efectuand integrala se va obtine :
. Inlocuind si efectuand integrala se va obtine :
P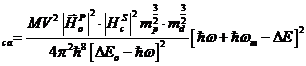 ,
, ![]() ; (56)
; (56)
![]() ,
, ![]() , (57)
, (57)
unde ![]() este masa efectiva a
golurilor in banda de valenta iar
este masa efectiva a
golurilor in banda de valenta iar ![]() masa efectiva redusa a electronilor in banda de conductie.
masa efectiva redusa a electronilor in banda de conductie.
Daca se presupun tranzitiile verticale de la ![]() premise,
premise, ![]() esteaproximativ
esteaproximativ ![]() . De asemenea
. De asemenea![]() poate fi si el exprimat cu ajutorul unui anumit model de
imprastiere al electronilor in banda de conductie pe vibratiile retelei:
poate fi si el exprimat cu ajutorul unui anumit model de
imprastiere al electronilor in banda de conductie pe vibratiile retelei:
15
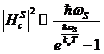 . (58)
. (58)
Inlocuind expresiile
lui ![]() si
si ![]() in (56) si luand
in (56) si luand ![]() , se gaseste probabilitatea:
, se gaseste probabilitatea:
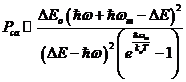 , (59)
, (59)
iar pentru coeficientul de absorbtie in cazul tranzitiilor indirecte prin I, cu absorbtia unui fonon :
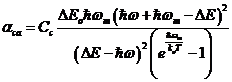 ,
, ![]() ; (60)
; (60)
![]() ,
, ![]() .
.
In mod asemanator se obtine contributia la absorbtie pornind de la termenul al doilea din (49) corespunzator emisiei unui fonon :
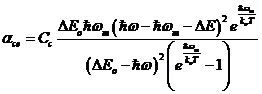 ,
, ![]() ; (61)
; (61)
![]() ,
, ![]() .
.
Coeficientii de absorbtie corespunzatori termenilor 3 si 4 din (49) se deduc in mod analog, iar expresiile lor sunt :
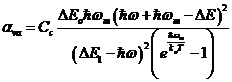 ,
, ![]() ; (62)
; (62)
![]() ,
, ![]() .
.
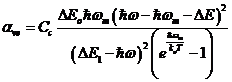 ,
, ![]() ; (63)
; (63)
![]() ,
, ![]() .
.
Coeficientul total de absorbtie se obtine prin sumare, adica:
16
![]() . (64)
. (64)
Absorbtia incepe la ![]() si fiecare termen este proportional cu diferenta dintre
energia fotonului si valoarea
si fiecare termen este proportional cu diferenta dintre
energia fotonului si valoarea ![]() la patrat.
la patrat.
Determinarile experimentale ale absorbtiei pe Ge si Si in regiunea limitei principale de absorbtie au aratat existenta tranzitiilor indirecte cu participarea a doua tipuri de fononi (acustici si optici),ale caror energii au putut fi determinate din masuratoride absorbtie.
In Ge absorbtia corespunzatoare fononilor optici este foarte slaba,pe cand in Si atit fononi acustici cat si cei optici aduc contributii apreciabile la absorbtie.
Ca ordin de marime,coeficientul de absorbtie datorat tranzitiilor indirecte este de 10 cm -1 , fata de 103 cm -1 in cazul tranzitiilor directe permise.
In regiunea pragului principal de absorbtie ,coeficientul de absorbtie depinde de temperatura si presiune prin intermediul lui ∆E, largimea zonei interzise. Dependenta de temperature si presiune a absorbtie poate fi determinata experimental,furnizand informatii asupra comportarii benzilor de energie. Tot in regiunea pragului se observa fenomene magneto-optice (fenmenul magnetoabsorbtiei oscilante) si electrooptice (efectul Frantz-Keldis), extreme de iteresante pentru precizarea cunostintelor asupra benzilor de energie .
|
Politica de confidentialitate |
| Copyright ©
2025 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |