
Calculul turatiei critice torsionale
Fenomenul de rezonanta care duce la pericolul de rupere a arborelui, se produce si atunci cand frecventa oscilatiilor momentului de rasucire coincide cu frecventa proprie a arborelui. Pentru calculul turatiei critice torsionale, se inlocuieste sistemul real cu un sistem cu un numar redus de mase.
Calculul arborelui cu diametru constant, cu un singur disc oscilant.

Sub actiunea momentului de rasucire Mt, dat de volantul fixat la
unul din capete, arborele incastrat rigid la celalalt capat se
rasuceste cu unghiul ![]() (figura 5.11).
(figura 5.11).
In momentul disparitiei acestui moment, intervine efectul cuplului de sens contrar, dat de fortele elastice din arbore. Ecuatia diferentiala a miscarii oscilante care se produce este:
 (5.48)
(5.48)
a carei solutie are forma:
q= A coswt + B sinwt =0 (5.49)
S-a notat aici cu I - momentul de inertie al masei volantului, iar cu c,- rigiditatea arborelui data de relatia :
![]() (5.50)
(5.50)
Dubla diferentiere a expresiei (5.49) si introducerea rezultatului in relatia (5.48) duce la relatia cunoscuta:
![]() (5.51)
(5.51)
Pentru un volant cu diametrul de inertie Di,
![]()
![]() (5.52)
(5.52)
relatie in care Gv inseamna greutatea volantului si g - acceleratia gravitationala.
Daca in expresia generala a momentului de inertie al masei oscilante:
![]() ,
,
in care dm este un element de masa la distanta r fata de axa, se inlocuieste raza de inertie ri , se obtine:
I = m ,,
m , avand denumirea de masa redusa.
Daca arborele are diametre in trepte d1, d2, ..., dn, pe lungimile corespunzatoare l1, l2, .., ln, luand ca diametru de baza d1 pentru arborele echivalent si aplicand in mod logic relatiile:

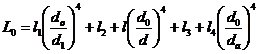 ,
,
deformatia arborelui are marimea:
 (5.53)
(5.53)
Arborele cu diametru constant si cu doua discuri oscilante.
Discurile
cu diametrele D1, D2 si momentele de
inertie I1, I2 se afla la
distanta l(fig. 5.12). Aplicarea ecuatiei momentelor de miscare
duce la concluzia ca cele doua mase nu pot oscila decat una contra
celeilalte, si deci la constatarea existentei unui punct de repaus pe
axa arborelui(sectiune neutra n-n,
la distantele l1, l2
fata de cele doua mase). Ca urmare, pentru fiecare parte de arbore
cu rigiditatea ![]() si
si ![]() se poate scrie:
se poate scrie:
 (5.54)
(5.54)
si I1l1 = I2l2 = I2(l - l1)
sau
![]() (5.55)
(5.55)
|
Fig.5.12 |
Tinand seama ca:
![]() si
si ![]() ,
,
in care G este modulul de elasticitate
transversala si ![]() modulul de
inertie polar al arborelui, din relatiile (5.54) si (5.55) se
deduce:
modulul de
inertie polar al arborelui, din relatiile (5.54) si (5.55) se
deduce:

sau
 (5.56)
(5.56)
Momentele de inertie masice I1 si I2
pot fi inlocuite prin masele reduse ![]() si
si ![]() .
.
|
Politica de confidentialitate |
| Copyright ©
2026 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |