Ne propunem sa rezolvam problema intalnirii a doua corpuri ce se deplaseaza pe aceeasi traiectorie circulara cu viteze si acceleratii diferite.
Applet-urile de sub link-ul "Cinematica" din cadrul programului "Fisica".
Definitie: Se numeste miscare circulara, miscarea a carei traiectorie este un cerc.
Se considera un cerc si un corp care se misca pe acesta, ca in figura de mai jos.
 La momentul
La momentul ![]() corpul se afla in punctul
corpul se afla in punctul
![]() caracterizat de
unghiul
caracterizat de
unghiul ![]() pe care raza
pe care raza ![]() il face cu raza
il face cu raza ![]() .
.
Coordonata unghiulara ![]() ,exprimata in radiani, are urmatoarea expresie in functie de
raza
,exprimata in radiani, are urmatoarea expresie in functie de
raza ![]() si arcul de cerc
si arcul de cerc ![]() :
: ![]()
Corpul ajunge in punctul
![]() la momentul
la momentul ![]() , iar pozitia lui poate fi precizata in functie de raza
, iar pozitia lui poate fi precizata in functie de raza ![]() si unghiul pe care
aceasta il face cu raza
si unghiul pe care
aceasta il face cu raza ![]() ,
, ![]() .
.
In cele ce urmeaza vom
considera ![]() , o functie de doua ori derivabila in raport cu timpul.
, o functie de doua ori derivabila in raport cu timpul.
Putem defini acum viteza unghiulara medie, ca fiind: ![]()
La fel ca in cazul miscarii rectilinii, vom defini viteza unghiulara instantanee:
![]()
Daca la momentul t corpul din figura 2 aflat in miscare
are viteza unghiulara ![]() si la momentul
si la momentul ![]() , viteza
, viteza ![]() , spunem ca acceleratia
unghiulara medie este:
, spunem ca acceleratia
unghiulara medie este: ![]() .
.
 Ca si in cazul vitezei unghiulare, expresia acceleratiei unghiulare instantanee
este:
Ca si in cazul vitezei unghiulare, expresia acceleratiei unghiulare instantanee
este:
![]()
Plecam de la expresia acceleratiei unghiulare pentru a determina legea miscarii circulare uniforme.
![]()
De unde putem scrie ca:
![]()
Integram relatia pe
intervalul finit ![]() si obtinem:
si obtinem:

Rezulta: 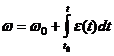 , (1)
, (1)
legea vitezei
Mai departe integram viteza unghiulara: ![]()
Analog cu prelucrarea expresiei acceleratiei, pentru pozitia unghiulara obtinem:
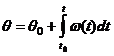 (2)
(2)
Figurile 3 si 4 reprezinta interpretarea geometrica a integralelor (1) si (2).
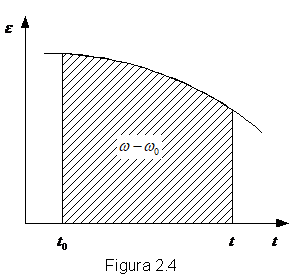
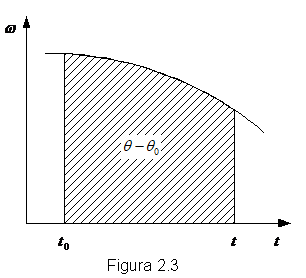
Miscarea circulara uniforma reprezinta miscarea unui corp cu viteza unghiulara constanta.
Analog miscarii rectilinii uniforme, ecuatiile miscarii circulare uniforme sunt:
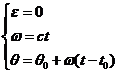 (3)
(3)
Graficul MCU este prezentat in figura 5.

Miscarea circulara uniform variata reprezinta misczrea unui corp pe o traiectorie circulara si cu acceleratie unghiulara constanta.
Tinand cont ca: 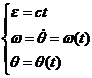
Obtinem prin rezolvarea
integralei (2), ![]() , legea vitezei in
MCUV.
, legea vitezei in
MCUV.
Consideram ![]() in relatia de mai sus
si integram intre aceleasi limite pentru a obtine legea miscarii circulare uniform variate:
in relatia de mai sus
si integram intre aceleasi limite pentru a obtine legea miscarii circulare uniform variate:
![]() (4)
(4)
Doua corpuri se deplaseaza pe circumferinta aceluiasi cerc. Se se determine locul si momentul in care cele doua corpuri se intalnesc. Parametrii ce descriu miscarile corpurilor sunt date in tabelul de mai jos.

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Politica de confidentialitate |
| |
Copyright ©
2025 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |