
STATICA STRUCTRILOR CONTINUE TIP PLACA
1 Elemente si ansambluri structurale
1.1 Parametri proprii si structurali
Structuri modelabile cu elemente finite tip placa patrulatere
Elementul finit tip placa patrulater (plan), decupat artificial dintr-un perete structural este de grosime constanta t, avand modulul de elasticitate constant E si coeficientul lui Poisson ν, la care deplasarile extremitatilor (doua rotiri in jurul axelor situate in panul median, ce corespund incovoierii acesteia dupa doua directii ortogonale, si o translatie normala la planul median) se produc sub actiunea fortelor corespunzatoare (doua momente incovoietoare si una normala la planul sau median), figura 1.

Figura 1
Comportarea la deformare elastica a elementului finit tip placa patrulater poate fi studiata prin raportarea parametrilor proprii d1, … d12, f1, … f12, la un reper propriu, definit de axele ortogonale x, y, dispuse in planul median al acestuia, si axa z, dispusa normal la planul median al acesteia, posibil, cu originea in extremitatea 1 (figura 1).
Ecuatia de echilbru static a elementului finit de tip placa patrulater este data de relatiile 1.1
 (1.1)
(1.1)
sau in exprimare matriceala compacta
![]()
unde:![]() este matricea de rigiditate a elementului finit tip
placa patrulater raportata la parametrii proprii, d1, …, d12, f1, …, f12;
este matricea de rigiditate a elementului finit tip
placa patrulater raportata la parametrii proprii, d1, …, d12, f1, …, f12;
![]() - vectorul deplasarilor
extremitatilor a elementului finit tip placa patrulater sau
al parametrilor proprii principali, d1,
…, d12;
- vectorul deplasarilor
extremitatilor a elementului finit tip placa patrulater sau
al parametrilor proprii principali, d1,
…, d12;
![]() - vectorul
fortelor ce actioneaza la extremitatile elementului
finit tip placa patrulater sau al parametrilor proprii secundari, f1, …, f12.
- vectorul
fortelor ce actioneaza la extremitatile elementului
finit tip placa patrulater sau al parametrilor proprii secundari, f1, …, f12.
Componenetele matricei de rigiditate a elementului a elementului finit tip placa patrulater se stabilesc aplicand proceduri ale metodei elementului finit.
Compatibilitatea deplasarilor extremitatilor elementului finit tip placa patrulater cu deplasarile nodurilor de conectare ale structurii este asigurata.
Structurile modelabile cu elemente finite tip placa patrulatere se pot organiza dupa doua directii (cazul planseelor) si dupa trei directii (cazul rampelor pentru scari etc.).
Pentru fiecare nod i al unei structuri plane modelabila cu elemente finite tip placa patrulatere (cazul planseelor) se definesc cate trei parametri principali, D3i-2, D3i-1 si D3i, primul fiind definit ca rotire in jurul primei axe a reperului structurii acesteia (obisnuit X), al doilea ca rotire in jurul celei de a doua axe a reperului structurii (obisnuit Y) si al treilea ca deplasare de translatie dupa a treia axa a reperului structurii normala la planul median al acesteia (obisnuit Z); pentru o structura cu n noduri se definesc 3n parametri principali. Parametrii secundari corespunzatori sunt momentele nodale F3i-2, respectiv F3i-1 si forta nodala F3i; pentru o structura cu n noduri se definesc 3n parametri secundari.
1.2 Stabilirea prin MEF - formularea directa
a ecuatiei matriceale de echilibru static - cu raportare la parametrii proprii
a elementului finit tip placa patrulater
In MEF, stabilirea ecuatiei matriceale de echilibru static, raportata la parametrii proprii, pentru elementul finit tip placa plana patrulater, implica un proces de calcul etapizat:
Etapa 1.1.1. Identificarea problemei.
Fie elementul finit de tip placa plana patrulater de grosime constanta t, caracterizat de modulul de elasticitate constant E si coeficientul lui Poisson ν, dispus in planul sistemului de referinta propriu xyz, aflat cu originea in extremitatea 1, deplasarile si fortele actionand la extremitatile sale (figura 1).
Problema consta in gasirea, in sistemul propriu de referinta, a unei relatii de legatura intre deplasarilor extremitatilor placii (d1, , d12) si fortele corespunzatoare (f1, , f12) de forma data de relatia E1.1.1.
![]() (E1.1.1)
(E1.1.1)
Etapa 1.1.2. Gasirea functiei, convenabile, de aproximare a deplasarilor d(x,y).
Se face ipoteza ca pe toata suprafata placii plane deplasarea transversala w(x,y) este data de o functie parabolica de gradul 4 (polinomiala), iar rotirile θx(x,y) si θy(x,y) sunt date de functii obtinute prin derivarea functiei deplasare transversala in raport cu y (si schimbarea semnului), respectiv x, totul putandu-se scrie simultan in forma matriceala data de relatia E1.1.2:

sau in forma compacta (E1.1.2)
![]()
unde ![]() este matricea functiilor de aproximare;
este matricea functiilor de aproximare;
![]() sunt coordonatele generalizate ale deplasarilor.
sunt coordonatele generalizate ale deplasarilor.
Etapa 1.1.3. Stabilirea relatiei matriceale dintre deplasarile punctuale si deplasarile extremitatilor elementului finit.
Se face afirmatia ca relatia E1.1.2 este valabila inclusiv in extremitatile elementului finit; aceasta se poate scrie simultan sub forma matriceala:

de unde rezulta:
![]()
care, prin inlocuire in relatia E1.1.2 conduce la la relatia E.1.1.3

sau in forma compacta, la (E1.1.3)
![]()
unde N1(x,y), , N12(x,y) sunt functiile de forma ale elementului finit tip placa patrulater.
Functiile de forma sunt functii de pondere, avand proprietatea de a lua valoare maxima (unitara) in extremitatea in care actioneaza parametrul principal aferent, restul functiilor de forma, aferente celorlalati parametri principali, avand valoare minima (zero); suma tuturor functiilor de forma are valoare unitara.
In implementarea pe calculator a programelor bazate pe metoda elementului finit este importanta exprimarea functiei deplasarilor prin intermediul functiilor de forma.
Etapa 1.1.4. Stabilirea relatiei matriceale dintre componentele ce definesc starea de deformatie punctuala si deplasarile extremitatilor elementului finit.
Se pleaca de la definitia starii de deformare (a curburilor si curburii de torsiune) din teoria elasticitatii aplicata placilor plane, relatia E1.1.4

sau in forma compacta (E1.1.4)
![]()
Etapa 1.1.5. Stabilirea relatiei matriceale dintre componentele ce definesc starea de tensiune punctuala si deplasarile extremitatilor elementului finit.
Se pleaca de la legea fizica a deformarii din teoria elasticitatii aplicata placilor plane, relatia E1.1.5

sau in forma compacta (E1.1.5)
![]()
Etapa 1.1.6. Stabilirea relatiei matriceale dintre deplasarile extremitatilor elementului finit si fortele corespunzatoare.
Se pleaca de la definitia lucrului mecanic virtual, exprimarea in deplasari virtuale (aplicat intregii suprafete a placii), pentru cel interior:

respectiv exterior:
![]()
si se impune egalitatea lor pentru existenta echilibrului static (Lint Lext
Dupa egalarea celor doi termeni si efectuarea simplificarilor (considerand ca nu toate deplasarile virtuale sunt egale cu zero) si pentru cazul particular al elementului plan rectangular, se obtine relatia E1.1.6

sau in forma compacta: (E1.1.6)
![]()
Integralele, continute de relatia E1.1.6, pot fi rezolvate fie aproximativ, prin integrari numerice dupa doua directii, fie exact (si in aceasta situatie este posibil), prin inlocuirea termenilor si efectuarea operatiilor indicate, in final obtinandu-se pentru matricea de rigiditate urmatoarele componente:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]()
![]()
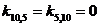
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
In felul acesta am definit elementul finit tip placa (plana) patrulater, din categoria elementelor finite bidimensionale (2D).
2 Statica matriceala pentru analiza planseelor
2.1 Stabilirea ecuatiei matriceale de echilibru static a elementului finit tip placa
Cazul structurilor modelabile cu elemente finite dreptunghiulare
Stabilirea ecuatiei de echilibru static pentru elemental finit curent e, al uni planseu implica parcurgerea unui proces etapizat de calcul.
Etapa 1.1. Stabilirea ecuatiei maticeale de echilbru static prin raportare la parametrii proprii, cu proiectia acestora in sistemul de referinta propriu xy, (in aceasta etapa notatiile utilizeaza minuscule si indicele p pentru sistemul de referinta propriu), relatia E1.1

sau (E1.1)
![]()
Etapa 1.2. Stabilirea ecuatiei matriceale de echilibru static prin raportare la parametrii structurali aferenti, cu proiectia acestora in sistemul de referinta unic, XY (in aceasta etapa notatiile utilizeaza majuscule si indicele S pentru sistemul de referinta structural , relatia E1.2,

sau (E1.2)
![]()
unde indicele inferior e indica apartenenta parametrului la elemental curent iar indicele superior e cota parte corespunzand elementului curent.
Parametrii proprii ai extremitatilor placii plane sunt proiectati pe directiile parametrilor structurali aferenti ai nodurilor corespunzatoare cu ajutorul matricei de transformare prin rotire, T, care are ca elemente componente cosinusii directori ai axelor proprii (xy) definiti functie de reperul structurii (XY). In cazul placilor plane pentru care sistemele proprii ale elementelor finite coincid cu sistemul structural, matricea de transformare prin rotire este matricea unitara.
Matricea T este o matrice ortogonala si are proprietatea ca inversa este egala cu transpusa:
![]()
Relatiile de legatura pentru parametrii raportati la sistemul propriu si parametrii raportati la sistemul structurii sunt:
![]()
![]()
care, inlocuite in relatia E1.1 si operat corespnzator, conduc la stabilirea matricei de rigiditate a saibei raportata la parametrii structurali aferenti:
![]()
Etapa 1.3. Stabilirea ecuatiei matriceale de echilbru static prin raportare la parametrii structurii, completand cu ecuatii fictive corespunzatoare parametrilor structurii ce nu sunt aferenti sau nu apartin saibei (in aceasta etapa notatiile utilizeaza majuscule sau indici referitori la apartenenta la elementul curent):

sau (E1.3)
![]()
unde:[K] este matricea de rigiditatea a elementului finit de tip saiba raportata la parametrii structurali.
2.2 Analiza statica a placii plane
Enuntarea problemei: Sa se efecteze analiza statica a placii plane modelata cu elemente finite tip placa plana patrulater (determinarea deplasarilor, fortelor din reazeme si eforturilor), schema statica, caracteristicile geometrice si mecanice, precum si incarcarile fiind precizate pe figura 2.
Rezolvarea problemei
Exceptand modul in care este stabilita ecuatia de echilibru static a placii plane raportata la parametrii proprii, Etapa 1, restul etapelor de calcul pentru rezolvarea problemei, urmaresc procesul etapizat, al metodei staticii matriceale clasice, pentru analiza structurilor cu bare, asa cum se va putea observa parcurgand aplicatia la problema enuntata.
Aplicatia utilizeaza notatii pentru variabile si operatori specifice programului de calcul matematic Mathcad (simbolul := are intelesul de atribuire).
Sistemul de referinta propriu este ales acelasi pentru toate elementele finite si identic cu sistemul de referinta al intregii structuri.
Figura 2
|
Politica de confidentialitate |
| Copyright ©
2025 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |