
Obtinerea unor performante dinamice bune, presupune controlul si comanda precisa a cuplului electromagnetic dezvoltat de motor. Aceasta se realizeaza, in cazul motorului de c.c. cu excitatie separata, prin controlul si comanda curentului din indus. Din punct de vedere fizic, in cazul tuturor motoarelor electrice, cuplul electromagnetic dezvoltat, fiind rezultatul interactiunii dintre un curent si un flux magnetic (de excitatie), va fi dat de produsul vectorial dintre cele doua marimi:
![]() . )
. )
In cazul motorului de c.c., cele doua marimi sunt ortogonale constructiv si deci produsul vectorial devine produs scalar si mai mult, el are valoare maxima:
![]() . (3. )
. (3. )
Astfel, daca fluxul de excitatie este mentinut constant (prin mentinerea constanta a curentului de excitatie), cuplul electromagnetic dezvoltat de motorul de c.c. poate fi controlat prin intermediul curentului din indus.
In cazul motorului asincron, se va exprima cuplul electromagnetic dezvoltat, sub forma unui produs vectorial dintre un flux si un curent, urmarindu-se apoi exprimarea sa in functie de doi curenti, acestia fiind masurabili si controlabili. In continuare, prin exprimarea cuplului electromagnetic in functie de curentii raportati in diferite sisteme de coordonate, se vor obtine forme ce vor permite implementarea schemelor de reglare vectoriala. In plus, urmarindu-se simplificarea expresiilor, exprimarea se va face in functie de marimi reciproc ortogonale, ceea ce va determina transformarea produsului vectorial in produs scalar. Din punct de vedere fizic, in functionare, pastrarea prin comanda a ortogonalitatii dintre marimile ce intervin, va asigura valori maxime ale cuplului dezvoltat, pentru aceleasi valori ale curentului.
Pentru obtinerea expresiei cuplului electromagnetic dezvoltat de motorul asincron, se considera ecuatiile de tensiuni, sub forma fazoriala, scrise in sistemul de referinta fix, solidar cu statorul Error! Reference source not found..a, Error! Reference source not found..b:
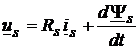 ,
,
![]() .
.
Componenta (-jwrY'r) din ecuatia de tensiuni rotorice, este o tensiune electromotoare de rotatie si corespunde puterii mecanice aferenta cuplului electromagnetic dezvoltat, me:
![]() . (3. )
. (3. )
Ca exprimare fazoriala insa, puterea transmisa printr-un circuit este:
![]() , )
, )
in care i* este complex-conjugatul curentului din circuit. Tinand cont de (3.4), puterea transmisa prin tensiunea electromotoare de rotatie se poate scrie
![]() ,
,
rezultand
![]() ,
,
iar cuplul electromagnetic:
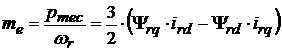 . (3. )
. (3. )
Expresia obtinuta reprezinta dezvoltarea expresiei vectoriale:
![]() . (3. )
. (3. )

Intr-adevar,
considerand, in sistemul de coordonate fix, solidar cu statorul, fazorii Y'r
si i'r oarecare (fig. 3.1), produsul lor vectorial este:
 . (3. )
. (3. )
Pentru o masina cu P perechi de poli, expresia cuplului electromagnetic dezvoltat este
![]() . )
. )
Inlocuind expresia fazorului fluxului rotoric in functie de fazorii curentilor statorici si rotorici Error! Reference source not found..c, cuplul electromagnetic se exprima:
![]() . )
. )
Obs. S-a tinut cont ca (i'r x i'r = 0), deoarece a
Considerand acum expresia fazorului fluxului statoric Error! Reference source not found..c, cu observatia de la , cuplul electromagnetic dezvoltat de motorul asincron se poate scrie:
 . )
. )
Neglijand saturatia magnetica, relatia este similara expresiei cuplului electromagnetic dezvoltat de masina de c.c. , iar daca, prin comanda, fazorii Ys si i'r sunt mentinuti ortogonali, produsul vectorial devine produs scalar si in plus, are valoare maxima.
In continuare, se vor prezenta expresiile cuplului electromagnetic in sistemele de referinta particulare (solidare cu fazorii fluxurilor rotoric, statoric, de magnetizare), in care dealtfel se va realiza comanda. Pentru aceasta, in mod similar obtinerii ecuatiilor de tensiuni, se va deduce expresia cuplului electromagnetic in sistemul general de coordonate (x, y), ce se roteste cu viteza oarecare wg, urmand ca expresia obtinuta sa fie particularizata pentru fiecare sistem de coordonate.
Se urmareste transcrierea expresiei , in functie de aceiasi fazori, dar exprimati in sistemul general de coordonate. Astfel, tinand cont de Error! Reference source not found..c si Error! Reference source not found..c, se obtine:
![]() . )
. )
Similar pentru fazorul curentului rotoric:
![]() . )
. )
Expresiile (3.11), evidentiaza faptul ca ambii fazori ce intervin in , fiind exprimati in sistemul general de coordonate, sunt rotiti cu acelasi unghi qg si deci produsul vectorial ramane acelasi, invariant fata de sistemul de coordonate ales:
![]() . (3. )
. (3. )
Similar pot fi transcrise expresiile si , respectiv:
![]() , )
, )
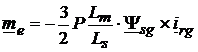 . (3. )
. (3. )
Prin inversarea ordinii produsului vectorial, (3.14) se poate scrie
![]() , )
, )
Exprimand fazorul fluxului statoric Ysg
![]()
si tinand cont ca isg x isg = 0, se obtine:
![]() . )
. )
O alta expresie se poate obtine daca se exprima fazorul fluxului rotoric Yrg
![]() ,
,
din care se expliciteaza irg si se inlocuieste in (3.16), cu observatia ca isg x isg = 0, rezultand:
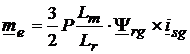 . )
. )
Au fost obtinute diferite expresii pentru cuplul electromagnetic dezvoltat de motorul asincron, toate insa fiind deocamdata sub forma unui produs vectorial. Se urmareste insa, scrierea sub forma unui produs scalar, ce se poate face daca termenii ce intervin sunt ortogonali. Aceasta va permite separarea efectelor componentelor curentului, respectiv, identificarea componentei reactive (generatoare de flux) si a componentei active (prin intermediul careia se va controla cuplul dezvoltat de motor). Din punct de vedere formal, se poate obtine separarea componentelor, daca se considera sisteme de referinta particulare, respectiv solidare cu fluxul rotoric, statoric sau rezultant (de magnetizare). Fiecare dintre acestea este echivalent cu considerarea unui sistem de referinta solidar cu curentul de magnetizare corespunzator.
Se considera expresia vectoriala a cuplului electromagnetic (3.18) scrisa in sistemul general de coordonate, a carei proiectie pe axele (x, y) ale sistemului general de coordonate conduce la
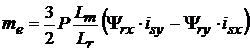 . )
. )
Se va considera acum un sistem rotitor de coordonate, solidar cu fluxul rotoric (fig. 3.2) si orientat in permanenta astfel incat componenta dupa axa y a fluxului rotoric sa fie nula (Yry Yrx Yr|). In acest caz, cuplul electromagnetic dezvoltat (3.19) va fi determinat de interactiunea intre doua componente ortogonale: fluxul rotoric dupa axa x (Yrx) si curentul statoric dupa axa y (isy):
 . (3. )
. (3. )

De observat
ca ambele componente sunt exprimate fata de acelasi sistem
de coordonate.
Particularizarea transformarilor pentru sistemul de coordonate considerat se poate face presupunand ca acesta, fiind caracterizat de unghiul de pozitie rr fata de sistemul fix (sD, sQ), se roteste cu
![]() . )
. )
Prin particularizarea Error! Reference source not found..b si Error! Reference source not found..c pentru qg = rr se obtin:
![]() ,
,
 .
.
Cuplul electromagnetic (3.20) se poate scrie atunci
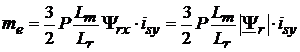 . )
. )
S-a obtinut astfel o expresie de produs scalar intre doua marimi (flux si curent) ortogonale, absolut similar motorului de c.c.
Pentru completare, se expliciteaza transformarea componentelor curentului statoric in sistemul solidar cu fluxul rotoric, transformare valabila pentru toate marimile statorice:
![]() ,
,
sau matriceal,
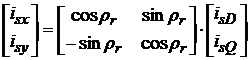 , (3. )
, (3. )
Evident ca transformarea inversa, din sistemul rotitor in sistemul fix va fi:
![]() ,
,
respectiv matriceal,
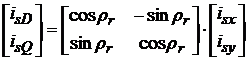 , )
, )
Deoarece marimile masurabile si controlabile sunt curentii, se va urmari ca sa se exprime in functie de curenti.
Pentru aceasta, expresiile curentului rotoric si ale fluxului rotoric in sistemul general de coordonate, Error! Reference source not found..b, respectiv Error! Reference source not found..b se particularizeaza pentru sistemul solidar cu fluxul rotoric:
![]()
![]()
![]() , )
, )
In sistemul de referinta solidar cu fluxul rotoric, ambele componente ale curentului rotoric (irx, iry) sunt nenule. Aceasta deoarece, in sistemul special, solidar cu fluxul rotoric, orientat cu axa x dupa acesta, fluxul rotoric dupa axa y este nul. In cazul in care iry ar fi nul, ar rezulta, conform proiectiei expresiei (3.25) pe cele doua axe, ca si isy sa fie zero. Cum insa isy este componenta generatoare de cuplu a curentului statoric, aceasta este in general nenula (chiar la mersul in gol), ceea ce inseamna ca pentru anularea componentei mutuale a fluxului rotoric datorata curentului isy, trebuie ca iry sa fie nenul.
In continuare se defineste curentul de magnetizare rotoric:
 . )
. )
Inductivitatea rotorica totala, Lr se poate exprima in functie de inductivitatile de dispersie rotorica si cea de magnetizare Lr = Lrs + Lm, sau definind factorul de dispersie al rotorului
 ,
,
curentul de magnetizare rotoric, se poate scrie
![]() .
.
Datorita alegerii particulare a sistemului de coordonate (solidar cu fluxul rotoric si orientat cu axa x dupa acesta), rezulta ca in acest sistem de coordonate, componenta fluxului rotoric dupa axa y va fi nula, ceea ce va determina, conform (3.26), ca si curentul de magnetizare rotoric sa nu aibe componenta decat dupa axa x:
 . )
. )
Explicitand modulul fluxului rotoric din (3.27) si inlocuind in expresia cuplului electromagnetic , se obtine:
 . )
. )
Aceasta ultima expresie obtinuta, permite evidentierea urmatoarelor aspecte:
cuplul electromagnetic este determinat de produsul scalar a doi curenti ortogonali;
in conditii de liniaritate (masina nesaturata magnetic), inductivitatile sunt constante, expresia cuplului dezvoltat de motorul asincron, este similara celei a cuplului dezvoltat de masina de c.c.
![]() ;
;
cuplul poate fi controlat prin comanda
independenta a celor doua componente, ![]() - generatoare de flux,
respectiv isy - generatoare de cuplu;
- generatoare de flux,
respectiv isy - generatoare de cuplu;
daca ![]() , atunci
, atunci ![]() , expresia cuplului electromagnetic devenind:
, expresia cuplului electromagnetic devenind:
 . )
. )
Aceasta se poate obtine daca se considera ecuatia de tensiuni rotorice, dupa axa x, pentru masina cu rotor in scurtcircuit
![]() .
.
In aceasta ecuatie nu apare componenta de rotatie datorata lui Yry deoarece aceasta componenta a fluxului rotoric este nula, prin alegerea sistemului de coordonate. Dar
![]() .
.
Daca ![]() , rezulta
, rezulta ![]() si in
consecinta irx = 0 si deci
si in
consecinta irx = 0 si deci
![]()
Schemele de reglare vectoriala bazate pe relatia (3.29) controleaza cele doua componente ortogonale ale curentului statoric astfel incat sa asigure mentinerea constanta a componentei reactive (isx), controlul cuplului realizandu-se prin intermediul componentei active, isy.
Se va particulariza expresia vectoriala a cuplului electromagnetic scrisa in sistemul general de coordonate. Tinand cont de expresiile fazorilor curentului statoric si ale fluxului statoric in sistemul general de coordonate, Error! Reference source not found..b, Error! Reference source not found..c, proiectia expresiei pe axele (x,y) ale sistemului general conduce la
![]() . (3. )
. (3. )
Daca s-ar considera un sistem de coordonate care sa fie solidar cu fluxul statoric, cu axa x orientata dupa acesta, va rezulta ca Ysy=0 si deci
![]() ,
,
ceea ce ar conduce la
![]() , )
, )
respectiv cuplul electromagnetic ar fi exprimat ca produs scalar a doua marimi ortogonale.
Pentru aceasta, se va particulariza sistemul general de coordonate pentru cazul cand acesta se roteste cu
![]() , (3. )
, (3. )

respectiv qg
= rs, axa x fiind orientata dupa fazorul
fluxului statoric (fig. 3.3).
Particularizand Error! Reference source not found..b si Error! Reference source not found..c pentru qg = rs se obtin:
![]() ,
,
![]() .
.
Cuplul electromagnetic (3.17), respectiv se poate scrie atunci
![]() . )
. )
S-a obtinut din nou o expresie de produs scalar intre doua marimi (flux statoric si curent) ortogonale, absolut similar motorului de c.c.
Pentru completare, se expliciteaza transformarea componentelor curentului statoric in sistemul solidar cu fluxul statoric, transformare valabila pentru toate marimile statorice:
![]() ,
,
sau matriceal,
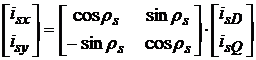 , (3. )
, (3. )
Evident ca transformarea inversa, din sistemul rotitor in sistemul fix va fi:
![]() ,
,
respectiv matriceal,
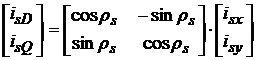 , (3. )
, (3. )
Deoarece marimile masurabile si controlabile sunt curentii, se va urmari, ca si in § 3.2, sa se exprime in functie de curenti.
Pentru aceasta, expresia fluxului statoric in sistemul general de coordonate Error! Reference source not found..a se particularizeaza pentru sistemul solidar cu fluxul statoric:
![]() , (3. )
, (3. )
in care fazorul curentului rotoric in sistemul solidar cu fluxul statoric se obtine prin particularizarea Error! Reference source not found..b pentru qg = rs
![]()
![]() .
.
Datorita alegerii particulare a sistemului de coordonate, se poate defini in continuare curentul de magnetizare statoric:
 . )
. )
Inductivitatea statorica totala, Ls se poate exprima in functie de inductivitatile de dispersie statorica si cea de magnetizare Ls = Lss + Lm, sau definind factorul de dispersie al statorului
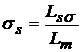 ,
,
curentul de magnetizare statoric, se poate scrie
![]() .
.
Datorita alegerii particulare a sistemului de coordonate (solidar cu fluxul statoric si orientat cu axa x dupa acesta), rezulta ca in acest sistem de coordonate, componenta fluxului statoric dupa axa y va fi nula, ceea ce va determina, conform (3.37), ca si curentul de magnetizare statoric sa nu aibe componenta decat dupa axa x:
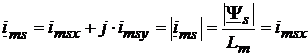 . )
. )
Explicitand modulul fluxului statoric din (3.38) si inlocuind in expresia cuplului electromagnetic , se obtine:
![]() . )
. )
S-a obtinut din nou o
expresie de produsul scalar a doi
curenti ortogonali, cuplul
putand fi controlat prin comanda independenta a celor doua
componente, ![]() - generatoare de flux,
respectiv isy - generatoare de cuplu. Se observa din nou
similaritatea cu expresia cuplului electromagnetic dezvoltat de motorul de c.c.
- generatoare de flux,
respectiv isy - generatoare de cuplu. Se observa din nou
similaritatea cu expresia cuplului electromagnetic dezvoltat de motorul de c.c.
Schemele de reglare vectoriala
bazate pe relatia (3.39) controleaza cele doua componente ortogonale ale curentului statoric
astfel incat sa asigure mentinerea constanta a componentei
reactive ![]() , controlul cuplului realizandu-se prin intermediul
componentei active, isy.
, controlul cuplului realizandu-se prin intermediul
componentei active, isy.
Daca in expresia cuplului electromagnetic , se exprima fluxul statoric total, ca suma a fluxurilor de dispersie si de magnetizare
![]() , )
, )
in care fazorul fluxului de dispersie statoric este
![]() ,
,
iar fluxul util
![]() , )
, )
cu ![]() si tinand
cont ca isg x isg = 0, rezulta
si tinand
cont ca isg x isg = 0, rezulta
![]() , )
, )
respectiv dupa dezvoltarea produsului vectorial:
![]() . (3. )
. (3. )
Expresia vectoriala a cuplului electromagnetic (3.42), scrisa in sistemul general de coordonate, se va particulariza pentru un sistem de coordonate solidar cu fazorul fluxului de magnetizare, ce are axa x orientata dupa fazorul fluxului si deci care se roteste cu
![]() , (3. )
, (3. )
in care mm reprezinta pozitia fazorului fluxului de magnetizare fata de sistemul fix de coordonate, solidar cu statorul (sD, sQ), fig. 3.4.

In acest
sistem de coordonate va rezulta ca Ymy=0 si deci
![]() ,
,
ceea ce conduce la
![]() , )
, )
respectiv cuplul electromagnetic este exprimat ca produs scalar a doua marimi ortogonale.
Pentru sistemul de coordonate considerat este valabila particularizarea qg = mm, ceea ce permite, pe baza expresiei Error! Reference source not found..b, obtinerea expresiei fazorului curentului statoric
![]() ,
,
iar prin particularizarea expresiei (3.40)
![]() .
.
Cuplul electromagnetic (3.42), devine atunci
![]() ,
,
respectiv
![]() . )
. )
S-a obtinut din nou o expresie de produs scalar intre doua marimi (flux statoric si curent) ortogonale, absolut similar motorului de c.c.
Pentru completare, se expliciteaza transformarea componentelor curentului statoric in sistemul solidar cu fluxul de magnetizare, transformare valabila pentru toate marimile statorice:
![]() ,
,
sau matriceal,
 , )
, )
Evident ca transformarea inversa, din sistemul rotitor in sistemul fix va fi:
![]() ,
,
respectiv matriceal,
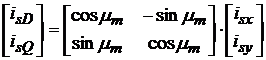 , )
, )
Ca si in cazurile anterioare (§ 3.2, § ), se va urmari sa se exprime in functie de curenti.
Pentru aceasta, expresia fluxului de magnetizare in sistemul general de coordonate (3.41) se particularizeaza pentru sistemul solidar cu fluxul statoric:
![]() , (3. )
, (3. )
in care fazorul curentului rotoric in sistemul solidar cu fluxul de magnetizare se obtine prin particularizarea Error! Reference source not found..b pentru qg = mm
![]() .
.
Inlocuind (3.48) in , se obtine:
![]() . )
. )
S-a obtinut din nou o
expresie de produsul scalar a doi
curenti ortogonali, cuplul
putand fi controlat prin comanda independenta a celor doua
componente, ![]() , respectiv imx - generatoare de flux si isy
- generatoare de cuplu. Se observa din nou similaritatea cu expresia
cuplului electromagnetic dezvoltat de motorul de c.c.
, respectiv imx - generatoare de flux si isy
- generatoare de cuplu. Se observa din nou similaritatea cu expresia
cuplului electromagnetic dezvoltat de motorul de c.c.
Schemele de reglare
vectoriala bazate pe relatia (3.50) controleaza cele doua componente ortogonale ale curentului statoric
astfel incat sa asigure mentinerea constanta a componentei
reactive ![]() , controlul cuplului realizandu-se prin intermediul
componentei active, isy.
, controlul cuplului realizandu-se prin intermediul
componentei active, isy.
|
Politica de confidentialitate |
| Copyright ©
2025 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |