
Elemente de teoria supraconductivitatii - Ecuatiile London
Dupa descoperirea efectului Meissnerm F. si H. London (1935) au propus sa se adauge ecuatiilor Maxwell relatii de material care sa permita explicarea efectului Meissner si a supraconductivitatii.
Intr-un material supraconductor se poate admite ca o parte din purtatorii de sarcina q formeaza, la temparaturi inferioare temperaturii critice, un fluid de densitate ns constanta. Acest fluid incarcat este nevascos (nu apar frecari). In aceste conditii, principiul doi al dinamicii aplicat unui purtator de sarcina supus actiunii campului electromagnetic conduce la:
![]() (12)
(12)
Adoptand descrierea Euler pentru fluid, acceleratia se poate scrie:
![]()
Folosind relatia vectoriala
![]()
se obtine
![]() (13)
(13)
Aplicand operatorul rot
ecuatiei (13) si tinand seama ca ![]() (ecuatia Maxwell
- Faraday) si ca rot grad =0, se obtine:
(ecuatia Maxwell
- Faraday) si ca rot grad =0, se obtine:
![]() (14)
(14)
Ipoteza lui London consta in a considera ca
![]() (15)
(15)
Introducand in ecuatia de miscare, rezulta:
![]() (16)
(16)
Atunci cand viteza este practic uniforma, ultimul termen din relatia (16) este nul si rezulta ecuatia "liniarizata":
![]() (17)
(17)
Densitatea de curent ![]() , numita frecvent supracurent, se exprima in
functie de campul electromagnetic din interiorul supraconductorului prin
relatiile:
, numita frecvent supracurent, se exprima in
functie de campul electromagnetic din interiorul supraconductorului prin
relatiile:
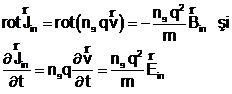 (18)
(18)
din care rezulta ecuatiile London:
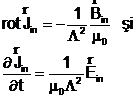 (19)
(19)
unde
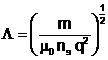 (20)
(20)
este un parametru cu dimensiunile unei lungimi, numit grosime London.
In regim cuasistationar,
termenul de deplasare din ecuatia Maxwell - Ampère (![]() ) este neglijabil, deci
) este neglijabil, deci
![]()
Cum ![]() , se obtine:
, se obtine:
![]() (21)
(21)
Din relatia (21) rezulta ecuatia diferentiala verificata de catre campul magnetic in interiorul supraconductorului:
![]() (22)
(22)
Pentru a preciza semnificatia fizica a ecuatiei diferentiale (22) vom considera un material supraconductor care ocupa semispatiul z>0, limitat de planul Oxy. In aceste conditii, ecuatia (22) devine:
![]()
a carei solutie acceptabila (fiind finita pentru orice valoare de z) este
![]() (23)
(23)
Campul se atenueaza
exponential. La o adancime de cateva ori mai mare decat ![]() campul devine practic
nul si efectul Meissner este total.
campul devine practic
nul si efectul Meissner este total.
|
Politica de confidentialitate |
| Copyright ©
2025 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |