
Momentul electromagnetic al motorului asincron trifazat
Potrivit digramei fazoriale a motorului asincron (fig.3.12) pentru puterea electromagnetica, transmisa rotorului masinii, este reala egalitatea:
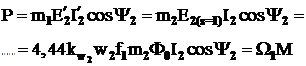 (3.37)
(3.37)
cu ![]() .
.
In consecinta, momentul electromagnetic al motorului asincron este:
![]() (3.38)
(3.38)
unde:
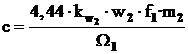 reprezinta o
marime constanta.
reprezinta o
marime constanta.
Din relatia (3.38)
rezulta, ca momentul de rotatie al motoului asincron este
proportional cu marimea fluxului magnetic![]() si cu componenta activa
si cu componenta activa ![]() a curentului din
infasurarea rotorului. Pe langa aceasta, daca se
porneste de la relatia (3.36) este adevarata egalitatea:
a curentului din
infasurarea rotorului. Pe langa aceasta, daca se
porneste de la relatia (3.36) este adevarata egalitatea:
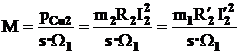 (3.39)
(3.39)
Daca in
ecuatia (3.39) se admite s=1 si se inlocuieste curentul ![]() cu curentul
cu curentul ![]() pentru pornirea
motorului se obtine expresia momentului la pornire:
pentru pornirea
motorului se obtine expresia momentului la pornire:
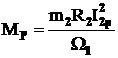 (3.40)
(3.40)
Toate motoarele asincrone se proiecteaza asa incat MP>Mn. Exceptie fac micromotoarele asincrone. Din expresia (3.40) rezulta ca pentru cresterea momentului de pornire, este necesara cresterea pierderilor in infasurarea rotorica. La motoarele cu inele de contact aceasta se realizeaza prin introducerea unui reostat de pornire in circuitul rotoric. Cu introducerea reostatului de pornire, se reduce insa marimea curentului rotoric. Iata de ce valoarea rezistentei reostatului de pornire trebuie sa fie astfel incat sa conduca la cresterea pierderilor din infasu-rarea rotorica, adica la cresterea momentului de pornire. In fig.3.15 prin diagrama fazoriala se prezinta influenta reostatului asupra momentului de pornire al moto-rului. Prezenta reostatului de pornire in circuitul rotoric are doua avantaje:
reduce curentul de pornire (I1p si I2p) sub o limita impusa;
cresterea factorului de putere
in circuitul rotoric, prin scaderea unghiului ![]() (fig.3.15), cu efect
asupra cresterii cuplului de pornire.
(fig.3.15), cu efect
asupra cresterii cuplului de pornire.
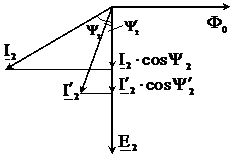
![]()
Fig.3.15 Diagrama fazoriala ce prezinta influenta reostatului
asupra momentului de pornire al motorului
Potrivit acestui procedeu, reostatul de pornire joaca rol dublu. El reduce curentul de pornire si creste momentul de pornire.
Daca in expresia (3.39) se substituie
valoarea lui ![]() din ecuatia (3.30)
si avand in vedere ca
din ecuatia (3.30)
si avand in vedere ca 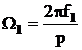 , se obtine ecuatia:
, se obtine ecuatia:
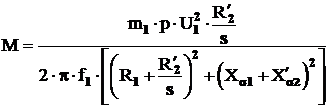 (3.41)
(3.41)
Din expresia (3.41) rezulta, ca momentul de rotatie al motorului asincron este proportional cu patratul tensiunii de alimentare.
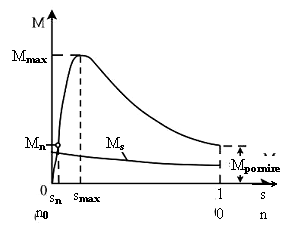
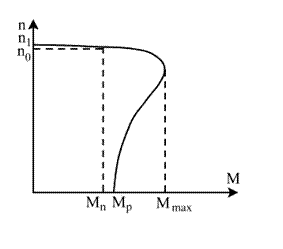
Dependenta M=f(s) sau, la alta scara n=f(M), in conditiile U1=cst=U1n; f1=cst.=f1n; R2p=0, poarta denumirea de caracteristica mecanica naturala (c.m.n). Aceste dependente sunt prezentate in fig.3.16 a, b.
a) b)
Fig.3.16 C.m.n. a masinii asincrone in regim de motor: a) M(s); b) n(M)
Valoarea alunecarii la care momentul motor atinge valoarea sa maxima, se determina din derivata (dM/ds) egalata cu zero. Aceasta se numeste alunecarea critica si este:
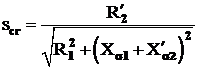 (3.42)
(3.42)
In mod obisnuit, R1<<![]() datorita careia
datorita careia
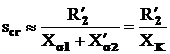 (3.43)
(3.43)
adica: momentul electromagnetic atinge
valoarea sa maxima, cand alune-carea devine egala cu raportul dintre
rezistenta activa raportata a rotorului ![]() si
reactanta inductiva XK
numita reactanta de scurtcircuit.
si
reactanta inductiva XK
numita reactanta de scurtcircuit.
Daca se inlocuieste valoarea lui scr in egalitatea (3.41), se obtine momentul maxim:
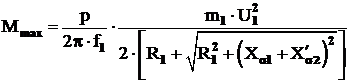 (3.44)
(3.44)
Din relatia (3.44) si ecuatia pentru scr rezulta, ca marimea rezistentei circui-tului rotoric nu influenteaza asupra valorii momentului maxim, insa determina alunecarea critica la care momentul atinge maximul sau.
La introducerea unei rezistente de
pornire mai mari (![]() ) in circuitul rotorului, creste si alunecarea
critica, adica
) in circuitul rotorului, creste si alunecarea
critica, adica 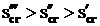 (fig.3.17).
(fig.3.17).
Din relatia (3.43) se
determina conditia de
obtinere a momentului de porni-re maxim. In acest scop, se considera
scr=1, la care ![]() =
=![]() , adica momentul de pornire are valoare maxima
cand rezistenta raportata a infasurarii rotorice
devine egala cu reactanta inductiva
, adica momentul de pornire are valoare maxima
cand rezistenta raportata a infasurarii rotorice
devine egala cu reactanta inductiva ![]() .
.
Relatia cu care se determina momentul de pornire se obtine daca in ecuatia (3.41) se considera s=1 sau
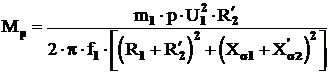
Pentru a porni un mecanism in sarcina
(utilaj), momentul de pornire al motorului asincron Mp trebuie sa fie mai mare decat momentul rezistent
Mr (fig.3.16). In caz
contrar se foloseste masina asincrona cu rotor bobinat si
reostat de pornire pentru cresterea momentului de pornire Mp. In fig.3.17, Mp este mai mare la
rezistenta ![]() a circuitului rotoric.
a circuitului rotoric.
Motoarele asincrone functioneaza stabil in portiunea ascendenta a caracteris-ticii M=f(s), adica in zona in care alunecarea s este in limitele de la s=0 pana la s=scr. Aici, la cresterea sarcinii cu cresterea alunecarii s (reducerea lui n), creste si momentul motor M, ca urmare a cresterii sarcinii.
In partea cazatoare a
caracteristicii M=f(s) adica pentru
![]() , motorul functioneaza instabil. Aici, la
cresterea sarcinii, cu cresterea alunecarii s (reduce-rea lui n) momentul motor M se reduce, ceea ce
conduce la oprirea masinii.
, motorul functioneaza instabil. Aici, la
cresterea sarcinii, cu cresterea alunecarii s (reduce-rea lui n) momentul motor M se reduce, ceea ce
conduce la oprirea masinii.
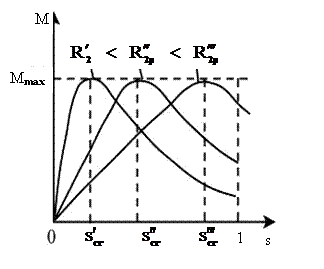
Fig.3.17 Variatia alunecarii critice in functie de rezistentele
introduse in circuitul rotorului motorului asincron cu rotor bobinat
|
Politica de confidentialitate |
| Copyright ©
2025 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |