
Reglarea automata a nivelului
A. Date initiale:
sectiunea rezervorului cilindric: S = 3m2;
presiunea din rezervor: p0 = 0,1kf/cm2;
densitatea lichidului al carui nivel se regleaza: r=0,8g/cm3;
debitul normal la iesire: Qe0 = 2m3 /min;
valoarea stationara a nivelului: h0 = 2m;
limitele de variatie a nivelului:
B. Continutul proiectului:
I. Generalitati
II. Alegerea schemei de reglare:
2.1. Descrierea functionarii schemei.
2.2. Prezentarea elementelor schemei.
III. Calculul constantelor de timp.
IV. Rezultate experimentale.
V. Bibliografie.
1. Generalitati
Se considera un rezervor cilindric inchis, de sectiune constanta, alimentat la partea superioara prin intermediul unei conducte avand debitul Qi .
La partea inferioara rezervorul este prevazut cu o conducta ce asigura evacuarea fluidului din rezervor, debitul de evacuare Qe fiind modificat prin intermediul unui ventil comandat.
Se cere sa se proiecteze un sistem de reglare care sa asigure mentinerea constanta a nivelului lichidului in rezervor, la o valoare impusa, prin comanda ventilului montat pe conducta de evacuare a rezervorului.
Se considera ca peturbatie a sistemului, fluctuatiile debitului de intrare in rezervor.
Convenim sa
notam cu ![]() valoarea impusa a
nivelului lichidului din rezervor.
valoarea impusa a
nivelului lichidului din rezervor.
Schema functionala de principiu a sistemului de reglare automata a nivelului intr-un rezervor inchis este prezentata in figura 1.

Fig.1 Schema functionala a sistemului de reglare automata a nivelului intr-un rezervor
2. Alegerea schemei sistemului de reglare
2.1. Descrierea functionarii schemei
Schema bloc a sistemului de reglare automata este prezentata in figura 2.

Fig.2 Schema bloc a sistemului de reglare automata
Asa cum se observa si din figura 2, in cadrul schemei de reglare apar urmatoarele elemente : regulatorul(R), elementul de executie (EE), procesul (P), traductorul (TR) si elementul de comparatie.
Iesirea (y) din procesul P este chiar marimea reglata, iar in cazul de fata este reprezentata de inaltimea lichidului din rezervor.
Marimea de iesirea y este masurata si convertita intr-un semnal unificat 4÷20 mA, prin intermediul traductorului. Marimea de iesire din traductor (r) este comparata, prin intermediul elementului de comparatie EC, cu marimea de referinta v, rezultand in final o eroare ε. Tinand cont de eroarea ε, regulatorul elaboreaza o marime de comanda c, de natura electrica, aceasta fiind convertita mai departe de catre un convertor electropneumatic intr-un semnal pneumatic care in cele din urma se aplica elementului de executie (EE). In conformitate cu comanda primita, elementul de executie modifica debitul de evacuare al rezervorului, astfel modficandu-se nivelul de lichid din rezervor.
Trebuie specificat faptul ca
marimea de referinta v, in cazul nostru fiind nivelul impus ![]() , este si ea
convertita in semnal unificat 4÷20 mA, prin
intermediul unui prescriptor de referinta.
, este si ea
convertita in semnal unificat 4÷20 mA, prin
intermediul unui prescriptor de referinta.
2.2. Prezentarea elementelor schemei
2.2.1. Elementul de executie
Atat pentru reglarea debitului, cat si pentru reglarea presiunii, cel mai folosit element de executie este ventilul cu membrana si resort, care este un element de executie comandat in presiune. Acesta poate fi comandat direct de catre un regulator pneumatic, insa in ultimul timp regulatoarele pneumatice sunt din ce in ce mai putin utilizate, locul lor fiind luat de regulatoarele numerice. In cazul utilizarii unui regulator numeric este necesara prezenta unui convertor electropneumatic care sa transforme marimea de comanda generata de regulator, marime care este de natura electrica, intr-o marime de natura pneumatica.
Concret, convertorul electropneumatic are ca marime de comanda un curent 4÷20 mA si furnizeaza, proportional cu acesta, un semnal pneumatic 0.2÷1bar. Pentru a putea fi realizata aceasta conversie este nevoie de o sursa de aer comprimat.
Schema functionala de principiu a unui ventil cu membrana si resort este prezentata in figura 3

Fig.3 Schema ventilului cu membrana si resort
Ventilul este compus din doua parti. O parte de actionare numita element de actionare (EA), care este alcatuit din camera 1 - in care se gaseste membrana elastica 2, de care sunt fixate rigid piesa metalica 3 si axul 4 - si resortul 5 care se opune deplasarii in jos a membranei si a axului 4.
Organul de reglare (OR), care reprezinta cea de-a doua parte a ventilului, este constituit din ventilul cu scaun simplu, a carei supapa 7 este solidara cu axul 4 al ventilului.
In functie de valorile marimii de comanda c, care este reprezentata printr-o presiune, axul 4 se deplaseaza in sus sau in jos, determinand deschiderea ventilului mai mult sau mai putin, in felul acesta realizandu-se modificarea debitului de fluid prin ventil.
Ecuatia diferentiala care leaga marimea de intrare in ventil (presiunea c) de deplasare l a axului ventilului este urmatoarea:
![]() , (1)
, (1)
unde:
M - masa pieselor in miscare;
n - coeficient de frecare vascoasa;
k - coeficient de elasticitate a resortului;
A - suprafata efectiva a diafragmei (membrana);
c - presiunea corespunzatoare comenzii generate de regulator;
c0 - presiunea in camera de aer a ventilului corespunzatoare pozitiei de echilibru a tijei.
Ecuatia pentru regimul stationar devine:
![]()
unde:
lst - valoarea deplasarii l, corespunzatoare regimului stationar;
cst - valoarea presiunii c, corespunzatoare regimului stationar.

In figura 4
este prezentata caracteristica deplasarii ventilului in functie
de marimea de comanda.
Fig. 4 Caracteristica ventilului cu membrana si resort
Pornind de la ecuatia (1) si tinand cont de faptul ca marimea de intrare in elementul de executie este presiunea pe diagrama iar marimea de iesire din elementul de executie este debitul prin ventil, a carui variatie este proportionala cu variatia deplasarii l a tijei, functia de transfer a elementului de executie este:
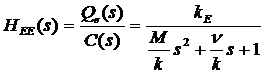 . (2)
. (2)
Pentru ca ventilul sa fie rapid trebuie
ca masa M sa fie mica, iar coeficientul de elasticitate sa fie
mare. Se observa ca raportul ![]() si deci, pentru
un astfel de ventil in practica se utilizeaza urmatoarea
functie de transfer a elementului de executie:
si deci, pentru
un astfel de ventil in practica se utilizeaza urmatoarea
functie de transfer a elementului de executie:
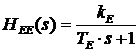 , (3)
, (3)
unde TE reprezinta constanta de timp a ventilului.
In aplicatiile uzuale TE < 3s.
In procesele cu constante de timp mari (Ti >>), in care Ti = 10 TE, se considera TE = 0 si astfel functia de transfer a ventilului poate fi considerata ca fiind HEE (s) = kE (element proportional).
In cazul proiectului nostru se considera TE=20s.
2.2.2. Stabilirea modelului matematic al procesului
Atunci cand rezervorul nu este deschis, si deci scurgerea lichidului nu este libera ci este influentata de presiunea p(t) formata in spatiul din bazin, neocupat de lichid, din ecuatia lui Bernoulli se va obtine formula de calcul a debitului de ietire Qe:
 , (4)
, (4)
unde r este densitatea lichidului.
Variatia volumului de lichid din rezervor este:
 . (5)
. (5)
Intrucat ecuatia (5) este neliniara, se va realiza o liniarizare in jurul valorilor de regim stationar.
Astfel, se considera ![]() ,
, ![]() ,
, ![]() ca fiind valorile de
regim stationar corespunzatoare marimilor
ca fiind valorile de
regim stationar corespunzatoare marimilor ![]() ,
, ![]() ,
, ![]() . Considerand ca marimile
. Considerand ca marimile ![]() ,
, ![]() ,
, ![]() prezinta
variatii foarte mici in jurul valorilor de regim stationar, vom avea:
prezinta
variatii foarte mici in jurul valorilor de regim stationar, vom avea:
 , (6)
, (6)
unde Dh(t), DQi(t) si DQe(t)
reprezinta abaterile marimilor ![]() ,
, ![]() ,
, ![]() fata de
valoarile de regim stationar.
fata de
valoarile de regim stationar.
Pornind de la ecuatiile (4) si (5) si liniarizand in jurul valorilor de regim stationar se va obtine:
![]() , (7)
, (7)
unde, pentru variatii suficient de mici s-a considerat:
 ;
;
![]() ;
;
![]() - variatia debitului
la iesire in raport cu nivelul;
- variatia debitului
la iesire in raport cu nivelul;
![]() - variatia debitului
la iesire in raport cu pozitia ventilului.
- variatia debitului
la iesire in raport cu pozitia ventilului.
Pentru a usura scrierea vom nota:


Ecuatia (7) devine:
![]() (8)
(8)
Privind procesul ca pe un obiect orientat , acesta poate fi reprezentat astfel:


Deci:  (9)
(9)
Inlocuind relatiile (9) in ecuatia (8), si tinand cont ca variatia debitului de iesire este proportionala cu variatia deplasarii l a tijei, vom obtine:
![]() (10)
(10)
Aplicand Transformata Laplace in conditii initiale nule, relatiei (10), obtinem:
![]() (11)
(11)
Facand cateva calcule matematice simple, se va obtine:
![]() (12)
(12)
unde:
 (13)
(13)
Din relatia (12), considerand perturbatia nula (P(s)=0), se va obtine functia de transfer a procesului in raport cu intrarea:
![]() (14)
(14)
Functia de transfer in raport cu perturbatia se va obtine tot din relatia (12), dar de data aceasta considerand intrarea nula:
![]() (15)
(15)
Punand in evidenta atat efectul marimii de intrare cat si efectul perturbatiei asupra iesirii, procesul poate fi reprezentat sub forma unei scheme bloc ca in figura 6:
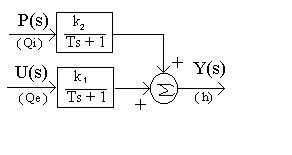
Fig. 6 Schema bloc a procesului de reglare.
Determinarea constantei de timp a procesului (T)
Conform ecuatiei lui Bernoulli avem:
 . (16)
. (16)
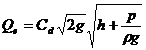 (17)
(17)
Termenul  reprezinta nivelul
echivalent al unei coloane de lichid ce ar corespunde cu presiunea din
rezervor. In acest caz ecuatia (17) devine:
reprezinta nivelul
echivalent al unei coloane de lichid ce ar corespunde cu presiunea din
rezervor. In acest caz ecuatia (17) devine:
![]() , (18)
, (18)
unde:
![]() ;
;
![]() .
.
In conditii de regim stationar ecuatia (18) devine:
![]() (19)
(19)
![]() (20)
(20)
Deci:
 . (21)
. (21)
Derivand relatia (21) in raport cu q o sa obtinem:
 (22)
(22)
Calculand valorile derivatei corespunzatoare regimului stationar obtinem:
 , (23)
, (23)
Tinand cont ca ![]() vom avea:
vom avea:
 . (24)
. (24)
Calculam hp0 utilizand datele initiale ale proiectului:
![]() (25)
(25)
Tinand cont de expresia lui T, data in relatia (13), rezulta:
 (26)
(26)
![]() (27)
(27)
2.2.4. Determinarea constantelor k1, k2 ,kEE:
Tinand cont de expresia lui k2, obtinem :
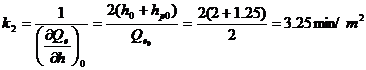 (28)
(28)
Intrucat se considera variatia debitului de iesire ca fiind proportionala cu variatia "l" a tijei ventilului si tinand cont ca marimea de intrare in ventil este un semnal unificat 4÷20 mA iar domeniul de variatie permis, in regim stationar, pentru marimea "h" este de 100 mm (in datele initiale se dau limitele permise de variatie ale nivelului ca fiind ±2.5% din valoarea stationara a nivelului, valoare care este de 2m; in urma unui calcul matematic simplu, domeniu de variatie al nivelului rezulta ca fiind de 100mm )rezulta:
![]() (28)
(28)
Constanta de proportionalitate a elementului de executie poate fi considerata kEE=1.
Traductorul
Se alege drept traductor de
nivel un nivelmetru de tipul ELT-30 care are domeniul de masura ![]() . Tinand cont ca iesirea traductorului este un
semnal unificat 4÷20 mA, constanta de proportionalitate a
traductorului va fi:
. Tinand cont ca iesirea traductorului este un
semnal unificat 4÷20 mA, constanta de proportionalitate a
traductorului va fi:
![]() (29)
(29)
Din datele initiale se stie ca in regim stationar variatia nivelului este de ±2.5%, adica:
![]() (30)
(30)
Intrucat ![]() apartine
domeniului
apartine
domeniului
![]() inseamna ca
traductorul ales corespunde cerintelor impuse.
inseamna ca
traductorul ales corespunde cerintelor impuse.
Functia de transfer a traductorului va fi:
![]() (31)
(31)
Schema bloc a sistemului de reglare automata in care este evidentiata atat functia de transfer a procesului in raport cu intrarea, cat si functia de transfer a procesului in raport cu perturbatia, este prezentata in figura 7:
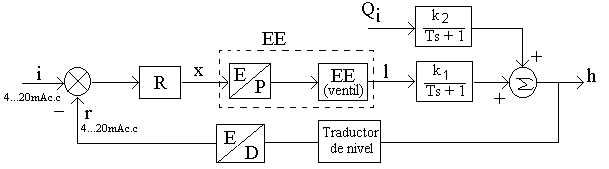
2.2.6. Alegerea si acordarea regulatorului
Se pune problema determinarii tipului de regulator utilizat pentru implementarea sistemului de reglarea automata a procesului dat. Fiind vorba de un reglaj de nivel, regulatorul se alege fie de tip P fie de tip PI.
Deoarece se admite o variatie de 2,5% a nivelului fata de valoarea de regim stationar si deci se admite o eroare stationara diferita de zero, se recomanda alegerea unui regulator de tip P.
Pentru acordarea regulatorului se utilizeaza criteriul Ziegler-Nichols. Conform acestui criteriu, factorul de proportionalitate kR al regulatorului se calculeaza cu formula:
![]()
unde ![]() reprezinta valoarea
factorului de amplificare pentru care sistemul oscileaza cu amplitudine
constanta (adica sistemul se afla la limita de stabilitate).
reprezinta valoarea
factorului de amplificare pentru care sistemul oscileaza cu amplitudine
constanta (adica sistemul se afla la limita de stabilitate).
Pentru calcularea
factorului ![]() se va utiliza
criteriul lui Bode.
se va utiliza
criteriul lui Bode.
Se calculeaza functia de transfer a sistemului in circuit deschis:
![]() (32)
(32)
Se determina caracteristicile logaritmice Bode:
![]() ; (33)
; (33)
![]() . (34)
. (34)
Din aceste caracteristici se
determina valoarea lui ![]() pentru care faza
raspunsului in frecventa este
pentru care faza
raspunsului in frecventa este ![]() .
.
Pentru aceasta valoare
a lui ![]() , notata cu wp , se determina modulul
raspunsului in frecventa:
, notata cu wp , se determina modulul
raspunsului in frecventa:
![]() .
.
Conform criteriului lui Bode
rezulta 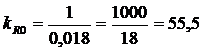 . Calculam acum valoarea
factorului de proportionalitate al regulatorului:
. Calculam acum valoarea
factorului de proportionalitate al regulatorului:
![]() . (32)
. (32)
IV. Rezultate experimentale
Simularea procesului se va realiza cu ajutorul programului MATLAB tinand cont de expresiile functiilor de transfer corespunzatoare blocurilor structurii de reglare:
functia de transfer a regulatorului: ![]() ;
;
functia de transfer a elementului de
executie: ![]() ;
;
functia de
transfer a traductorului:![]() ;
;
functia de transfer a procesului in raport cu intrarea:
![]()
functia de transfer a procesului in raport cu perturbatia:
![]() .
.
Cu aceste functii de transfer, schema de reglare folosita este prezentata in figura 8.

Figura 8
Fig. 8 Schema procesului de reglare folosita pentru simulare
Prescriptorul de referinta realizeaza conversia marimii de referinta, care este un nivel, in semnal unificat 4÷20 mA.
In figura 9 este prezentat raspunsul sistemului pentru o intrare treapta, aplicata la momentul t=0sec, respectiv pentru o perturbatie aplicata la momentul
![]()
In figura 10 este evidentiata doar influenta perturbatiei asupra evolutiei sistemului.
Asa cum se observa si din figura 9, nivelul lichidului din bazin a suferit o crestere de 3 metri, iar debitul de intrare (care este de fapt perturbatia sistemului) s-a marit cu 1,5 m3 /min.
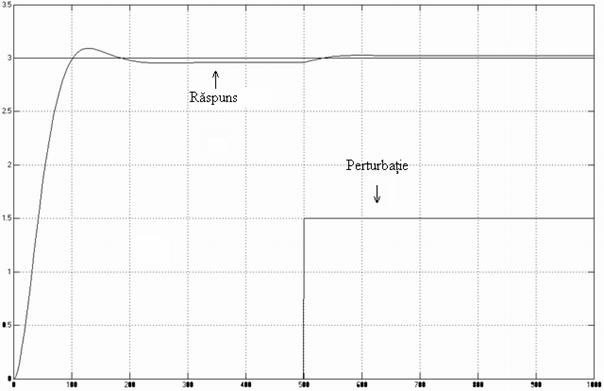

Fig. 9. Rezultatul simularii in MATLAB
Fig. 10. Influenta perturbatiei
Se observa ca in cazul modificarii referintei, sistemul trece printr-un regim tranzitoriu, prezetand un suprareglaj, dupa care se stabilizeaza la o valoare stationara, care este totusi diferita de cea a referintei. Acest lucru este explicat de faptul ca alegerea unui regulator de tip P nu asigura o eroare stationara nula, dar aceasta eroare se incadreaza in limitele admise.
|
Politica de confidentialitate |
| Copyright ©
2025 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |