
Simplificarea circuitelor logice cu harti Karnaugh
Exemplele de simplificare a circuitelor logice de pana acum puteau fi realizate la fel de bine si cu ajutorul algebrei booleene. Problemele de simplificare logica reale implica insa utilizarea unor harti Karnaugh mai mari. In aceasta sectiune vom concepe cateva exemple imaginare, lasand aplicatiile practice pentru capitolul de logica combinationala. Aceste exemple sunt concepute doar pentru a ilustra tehnicile de simplificare.
Vom folosi harta Karnaugh dezvoltata anterior, mai exact forma din dreapta:
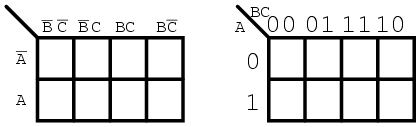
Observati secventa numerelor din partea superioara a hartii. Aceasta nu este o secventa binara (00, 01, 10, 11), ci este o secventa de tipul 00, 01, 11, 10. Aceasta secventa este cunoscuta sub numele de cod Gray. Secventa de tip cod Gray modifica doar un singur bit pe masura ce trecem de la un numar la urmatorul numar din secventa. Acest lucru nu este valabil intr-o secventa binara. Regiunile adiacente difera doar printr-un singur bit, sau variabila booleana. Acest lucru este necesar daca dorim organizarea iesirilor unei functii logice pentru observarea elementelor lor comune.
Mai mult, antetul coloanelor si randurilor trebuie sa fie in ordinea codului Gray, altfel, harta nu se va comporta precum o harta Karnaugh. Regiunile ce au in comun variabile booleene nu vor mai fi adiacente si nu vom mai putea identifica caracteristicile specifice functiei pe cale vizuala. Regiunile adiacente variaza cu un singur bit, deoarece secventa de cod Gray variaza la randul ei doar cu un singur bit.
Sa folosim in continuare hartile Karnaugh cu 3 variabile pentru simplificarea unor expresii booleene. Vom arata cum sa trecem termenii produs ai ecuatiei nesimplificate in harta Karnaugh. Vom ilustra si modul de identificare a grupurilor de regiuni adiacente ce duc la formarea sumei de produse simplificate a circuitului logic (expresiei booleene).

Dandu-se expresia (A'B'C' + A'B'C), primul pas este introducerea valorilor de 1 pe harta Karnaugh corespunzator pozitiei fiecarui produs al sumei (A'B'C' este echivalent cu 000, iar A'B'C este echivalent cu 001). Identificam apoi un grup de regiuni alaturate ce contin valori de 1 (in cazul de fata, avem doar doua astfel de regiuni). Scriem apoi produsul de termeni pentru acest grup, ceea ce reprezinta rezultatul simplificat.

Grupand cei patru termeni de 1 pe harta Karnaugh, rezultatul este asigurat de expresia A'.

Identic, grupand cei patru termeni de 1, putem foarte usor observa ca singura variabila ce acopera toate cele patru regiuni este C.
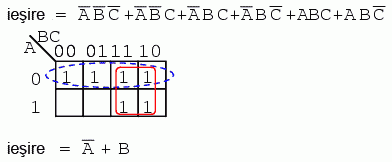
Din moment ce avem doua grupuri pe harta Karnaugh de mai sus, rezultatul va fi o suma de produse, si anume, A' + B.

Cele doua produse de mai sus formeaza un grup de doi termeni ce se simplifica la BC.

Variabila comuna celor patru termeni grupati mai sus este B
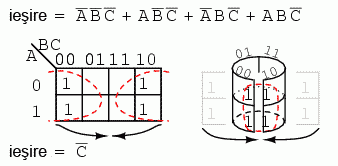
Cei patru termeni de mai sus formeaza un singur grup. Putem vizualiza acest grup daca "indoim" extremitatile hartii pentru a forma un cilindru. In acest caz, regiunile sunt adiacente. In mod normal, un astfel de grup se noteaza conform figurii din stanga. Din intregul set de variabile (A, B, C), singura variabila comuna este C'. C' este zero in toate cele patru regiuni. Acesta este atunci rezultatul final al simplificarii.

Cele sase regiuni rezultate din ecuatia nesimplificata pot fi organizate in doua grupuri de cate patru elemente. Aceste grupuri trebuie sa rezulte intr-o suma de doua produse, si anume A' + C'.
Sa reluam mai jos exemplul incineratorului de deseuri toxice studiat intr-un capitol precedent. Vom incerca simplificarea circuitului logic folosind o harta Karnaugh:

Ecuatia booleana de iesire este o suma de patru produse. Prin urmare, vom avea patru regiuni de 1 pe harta Karnaugh. Grupand regiunile adiacente, avem trei grupuri de cate doi termeni. Vom avea prin urmare o suma de trei produse, fiecare produs continand doi termeni. Circuitul logic simplificat, identic cu cel obtinut cu ajutorul regulilor de simplificare booleana, este redat mai jos:

Facand o comparatie intre regulile booleene folosite pentru simplificarea circuitului logic al incineratorului

si harta Karnaugh, care duce la exact acelasi rezultat

Putem lesne vedea motivul pentru care hartile Karnaugh sunt preferate pentru simplificarea circuitelor logice in detrimentul simplificarii booleene.
|
Politica de confidentialitate |
| Copyright ©
2025 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |