
Studiul osciloscopului catodic, Masurari in regim dinamic
Masurarea defazajului
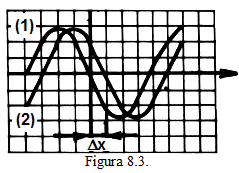 Doua semnale sinusoidale de
frecvente si amplitudini egale sunt vizualizate pe ecranul unui
osciloscop catodic cu doua spoturi (figura 8.3). Cunoscand
Doua semnale sinusoidale de
frecvente si amplitudini egale sunt vizualizate pe ecranul unui
osciloscop catodic cu doua spoturi (figura 8.3). Cunoscand ![]() si
latimea spotului
si
latimea spotului ![]() sa se determine
expresiile celor doua semnale si eroarea relativa la
determinarea defazajului, datorata dimensiunii spotului.
sa se determine
expresiile celor doua semnale si eroarea relativa la
determinarea defazajului, datorata dimensiunii spotului.
Amplitudinile celor doua semnale:
![]()
Valorile efective ale celor doua semnale:
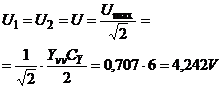
Frecventa semnalelor:
![]()
Defazajul dintre semnale:
![]()
Expresiile tensiunilor alternative vizualizate sunt:
![]()
![]()
Eroarea relativa la determinarea defazajului:
![]()
Masurarea frecventei
La intrarea Y a unui
osciloscop catodic se aplica semnalul sinusoidal produs de un generator
standard la care frecventa si amplitudinea sunt reglabile si au
valori cunoscute, iar sistemului de deflexie orizontala un semnal
sinusoidal de frecventa necunoscuta, ![]() . Se modifica coeficientul de deflexie pe verticala
si nivelul semnalului etalon pana cand imaginea se incadreaza
intr-un patrat determinat de liniile rastrului ecranului. Apoi se
regleaza frecventa la generatorul standard si se constata
ca pentru
. Se modifica coeficientul de deflexie pe verticala
si nivelul semnalului etalon pana cand imaginea se incadreaza
intr-un patrat determinat de liniile rastrului ecranului. Apoi se
regleaza frecventa la generatorul standard si se constata
ca pentru ![]() imaginea
imaginea
pe ecran este aceea a unei elipse care trece prin fazele prezentate
in figura .4.
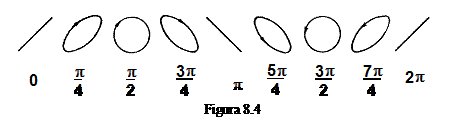
Se observa ca
intr-un interval de timp ![]() se desfasoara
5 astfel de cicluri complete. Sa se determine frecventa
necunoscuta
se desfasoara
5 astfel de cicluri complete. Sa se determine frecventa
necunoscuta ![]() .
.
Cele doua semnale aplicate pe canalele X si Y sunt:
![]()
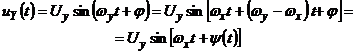
Cand cele doua
frecvente sunt foarte apropiate se poate considera ca semnalele au
frecvente egale, dar faza ![]() , variaza lent in timp.
, variaza lent in timp.
Daca se noteaza
cu ![]() momentul in care
elipsa degenereaza intr-un segment situat in cadranele 1 si 3 si
considerand
momentul in care
elipsa degenereaza intr-un segment situat in cadranele 1 si 3 si
considerand ![]() perioada
miscarii elipsei se poate scrie:
perioada
miscarii elipsei se poate scrie: ![]() din care rezulta:
din care rezulta:
![]() sau
sau ![]()
Deci:
![]()
Masurarea valorii efective si a perioadei
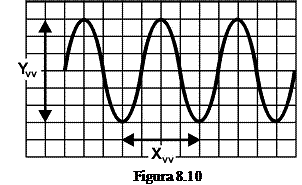 Pe ecranul unui osciloscop catodic se
vizualizeaza un semnal sinusoidal (figura 8.10) pentru care
Pe ecranul unui osciloscop catodic se
vizualizeaza un semnal sinusoidal (figura 8.10) pentru care ![]() diviziuni, iar
distanta dintre doua varfuri consecutive
diviziuni, iar
distanta dintre doua varfuri consecutive ![]() diviziuni. Fiind
cunos-cute, coeficientul de deviatie pe verticala
diviziuni. Fiind
cunos-cute, coeficientul de deviatie pe verticala 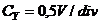 si co-eficientul
bazei de timp
si co-eficientul
bazei de timp ![]() sa se determine
valoarea efectiva a tensiunii alternative si frecventa acesteia.
sa se determine
valoarea efectiva a tensiunii alternative si frecventa acesteia.
Amplitudinea tensiunii alternative este:
![]()
Valoarea efectiva:
![]()
Perioada semnalului masurat:
![]()
Frecventa:
![]()
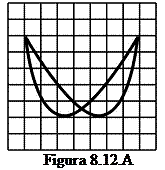 Unui osciloscop catodic avand coeficientul
de deflexie pe verticala
Unui osciloscop catodic avand coeficientul
de deflexie pe verticala ![]() si coeficientul
de deflexie pe orizontala
si coeficientul
de deflexie pe orizontala ![]() , i se aplica pe canalul Y un semnal sinusoidal
de frecventa
, i se aplica pe canalul Y un semnal sinusoidal
de frecventa ![]() , iar pe canalul X un alt semnal sinusoidal de
frecventa necunoscuta. Sa se determine expresiile celor
doua tensiuni, daca pe ecranul aparatului se obtine imaginea
stabila din figura 8.12.A. Se considera ca osciloscopul nu
introduce distorsiuni de faza.
, iar pe canalul X un alt semnal sinusoidal de
frecventa necunoscuta. Sa se determine expresiile celor
doua tensiuni, daca pe ecranul aparatului se obtine imaginea
stabila din figura 8.12.A. Se considera ca osciloscopul nu
introduce distorsiuni de faza.
Semnalele aplicate au expresiile:
![]()
Amplitudinea semnalului ![]() este:
este:
![]()
Amplitudinea semnalului ![]() :
:
![]()
Pe baza relatiei:
![]()
pentru figura Lissajous formata se deduce:
![]()
Deci:
![]()
![]()
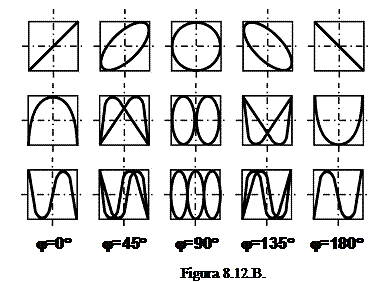
Tinand
seama ca figurile Lissajous depind si de defazajul dintre cele
doua tensiuni ![]() si
si ![]() asa cum se
prezint in figura 8.12.B. se deduce:
asa cum se
prezint in figura 8.12.B. se deduce: ![]()
Determinarea caracteristicilor magnetice ale unui material fero-magnetic.
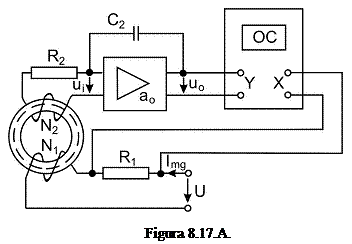 Pentru
determinarea caracteristicilor magnetice ale unui material fero-magnetic se
u-tilizeaza sche-ma prezentata in figura .a.
Pentru
determinarea caracteristicilor magnetice ale unui material fero-magnetic se
u-tilizeaza sche-ma prezentata in figura .a.
Pe un esantion toroidal realizat din
materialul studiat sunt re-partizate uni-form ![]() spire ale
infa-surarii de magnetizare alimentata de la o sursa
de tensiune alternativa cu frecventa
spire ale
infa-surarii de magnetizare alimentata de la o sursa
de tensiune alternativa cu frecventa ![]() . Pe acelasi circuit magnetic este dispusa
infasurarea de masurare a inductiei magnetice avand
. Pe acelasi circuit magnetic este dispusa
infasurarea de masurare a inductiei magnetice avand ![]() spire, la bornele sale
fiind conectat amplificatorul A cu factor de multiplicare in bucla deschisa foarte mare (
spire, la bornele sale
fiind conectat amplificatorul A cu factor de multiplicare in bucla deschisa foarte mare (![]() ). Tensiunea de la iesirea amplificatorului se
aplica canalului Y al osciloscopului catodic, in timp ce sistemului
de deflexie pe orizontala i se aplica tensiunea culeasa pe
rezistenta
). Tensiunea de la iesirea amplificatorului se
aplica canalului Y al osciloscopului catodic, in timp ce sistemului
de deflexie pe orizontala i se aplica tensiunea culeasa pe
rezistenta ![]() parcursa de
curentul de magnetizare
parcursa de
curentul de magnetizare ![]() . Pe ecranul osciloscopului apare o curba inchisa
care reprezinta
. Pe ecranul osciloscopului apare o curba inchisa
care reprezinta 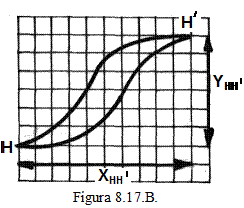 ciclul de histerezis magnetic al
materialului testat (figura 8.17.B).
ciclul de histerezis magnetic al
materialului testat (figura 8.17.B).
Circuitul
magnetic este realizat din ![]() tole, avand grosimea
tole, avand grosimea ![]() , diametrul exterior
, diametrul exterior ![]() si diametrul
interior
si diametrul
interior ![]() , iar den-sitatea materialului este:
, iar den-sitatea materialului este:
![]() .
.
Cunoscand valorile compo-nentelor schemei: ![]() ,
, ![]() ,
, ![]() si
coeficientii de deflexie pe verticala
si
coeficientii de deflexie pe verticala ![]() si pe
orizontala
si pe
orizontala ![]() sa se determine
inductia maxima
sa se determine
inductia maxima ![]() , intensitatea maxima a campului magnetic
, intensitatea maxima a campului magnetic ![]() si pierderile
specifice in fier.
si pierderile
specifice in fier.
Rezolvare
Din
legea circuitului magnetic: ![]() se deduce
se deduce ![]() , in care l semnifica lungimea unei linii medii
de camp magnetic:
, in care l semnifica lungimea unei linii medii
de camp magnetic:
![]()
Se poate scrie:
![]()
sau:
![]()
in care ![]() reprezinta
deviatia maxima pe orizontala a spotului osciloscopului
corespunzatoare ciclului de histerezis.
reprezinta
deviatia maxima pe orizontala a spotului osciloscopului
corespunzatoare ciclului de histerezis.
Numeric se obtine:
![]()
Deoarece ![]() rezulta:
rezulta:
![]()
Tensiunea indusa la bornele infasurarii de masurare este:
![]()
Considerand curentul de intrare in amplificator neglijabil, conform primei teoreme a lui Kirchhoff:
![]()
sau:
![]()
Tinand seama ca ![]() se obtine:
se obtine:
![]()
Deoarece factorul de amplificare are valoare foarte mare se poate scrie:
![]()
Deci:
![]()
![]()
Rezulta:
![]()
Sau:
![]()
in care ![]() reprezinta
deviatia maxima pe verticala a spotului, corespunzatoare
ciclului de histerezis:
reprezinta
deviatia maxima pe verticala a spotului, corespunzatoare
ciclului de histerezis:
![]()
Deoarece ![]() se obtine
se obtine
![]()
Pentru determinarea
pierderilor specifice de energie in esantion se exprima aria ciclului
de histerezis si se deduce succesiv ![]() in care:
in care:
![]()
![]()
![]()
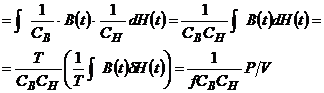
Aici V reprezinta volumul materialului feromagnetic.
Rezulta:
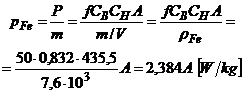
in care A se exprima in cm2.
|
Politica de confidentialitate |
| Copyright ©
2025 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |