Aritmetica booleana
Trebuie inteles inca de la inceput faptul ca numerele booleene nu sunt tot una cu numerele binare. Numerele booleene reprezinta un sistem matematic total diferit de cel al numerelor reale, pe cand notatia binara este doar atat: o notatie alternativa a numerelor reale. Cele doua sunt adesea confundate datorita faptului ca utilizeaza aceleasi cifre: 0 si 1. Diferenta consta in faptul ca valorile booleene sunt limitate la un singur bit (fie 0, fie 1), pe cand numerele binare pot fi compuse din mai multi biti.
Sa incepem asadar capitolul de algebra booleana prin adunarea numerelor:
0 + 0 = 0
0 + 1 = 1
1 + 0 = 1
1 + 1 = 1
Primele trei sume nu sunt deloc iesite din comun din punct de vedere al operatiei de adunare elementara. Ultima suma in schimb, s-a dovedit a fi responsabila de mai multa confuzie decat oricare alt element al electronicii digitale. Forma sa nu se supune principiilor de baza ale matematicii. Intr-adevar, aceasta contrazice principiile adunarii numerelor reale, dar nu si a numerelor booleene. In cadrul matematicii booleene exista doar doua valori posibile pentru oricare valoare si pentru orice operatie matematica: 0 sau 1. Nu exista valoarea "2". Din moment ce suma "1 + 1" nu poate fi 0, prin eliminare, aceasta suma trebuie sa fie 1.
De asemenea, nu conteaza nici cati termeni contine suma. Sa consideram urmatoarele sume, de exemplu:
Revenind la primul set de ecuatii, putem observa ca aceste sume nu sunt altceva decat tabelul de adevar al unei porti logice SAU. Cu alte cuvinte, adunarea booleana corespunde functiei logice a portii SAU, precum si comutatoarelor conectate in paralel:
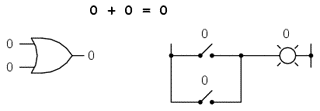
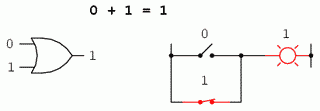
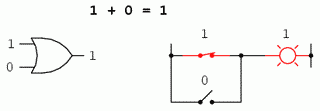
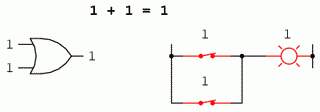
In cadrul matematicii booleene nu exista notiunea de scadere. Scaderea implica existenta numerelor negative: 5 - 3 este identic cu 5 + (-3), de exemplu. Dar in algebra booleana, nu exista valori negative (doar 0 si 1).
De asemenea, nu exista nici operatia de impartire booleana. Impartirea nu este altceva decat o scadere compusa, la fel cum inmultirea nu este altceva decat adunare compusa.
Inmultirea booleana este permisa, iar regulile sunt aceleasi cu inmultirea numerelor reale: orice numar inmultit cu 0 este 0, si orice numar inmultit cu 1 ramane neschimbat:
0 x 0 = 0
0 x 1 = 0
1 x 0 = 0
1 x 1 = 1
Setul de ecuatii ar trebui sa va fie cunoscut: sunt aceleasi reguli ce se regasesc in tabelul de adevar al portii SI. Cu alte cuvinte, inmultirea booleana corespunde functiei logice a portii SI, precum si comutatoarelor conectate in serie:
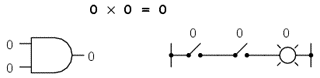
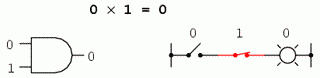
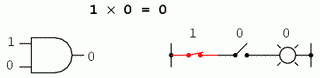
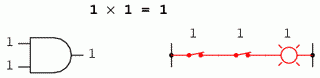
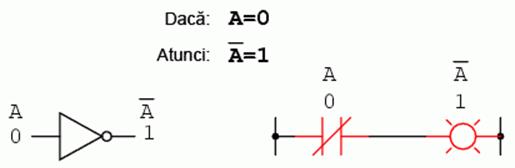
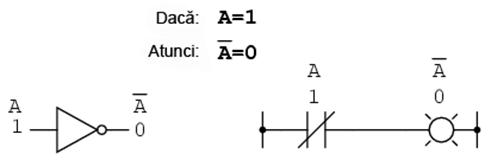
La fel ca si algebra "normala", algebra booleana utilizeaza litere pentru desemnarea variabilelor. Dar, fata de algebra "normala", aceste variabile se trec tot timpul cu majuscule. Datorita faptului ca exista doar doua stari posibile, fie 1, fie 0, fiecare variabila poseda si un complement: valoarea opusa a acesteia. De exemplu, daca variabila "A" este 0, atunci complementul ei este 1. Complementul se specifica prin intermediul unei linii orizontale deasupra variabilei, astfel:

Sub forma scrisa, complementul lui "A" este desemnat prin "A-negat". Cateodata se utilizeaza simbolul "'" pentru reprezentarea complementului (A'). De obicei insa, simbolul cu linie este mai folosit decat simbolul "'". Motivele le vom afla putin mai incolo.
Complementarea booleana este echivalenta cu o poarta logica NU, sau cu un contact normal-inchis:
|
Politica de confidentialitate |
| Copyright ©
2026 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |