
Masurarea puterilor active si reactive in circuite trifazate
1. Teorema
generalizata (Blondel) a masurarii puterilor active si
reactive prin
metoda celor n si n-1
wattmetre si varmetre
Se considera cazul general al unui receptor constituit din impedante liniare, bilaterale, formand o retea cu ochiuri care comporta n noduri, alimentata printr-un circuit polifazat cu n conductoare.
Puterea aparenta complexa totala S este egala cu suma puterilor aparente date de potentialele nodurilor V1, V2, ., Vn cu curentii de linie I1, I2, ., In:
![]() (3.277)
(3.277)
Daca se considera un punct N de un potential oarecare (figura 3.83 b) notand cu U1N, U2N, , UnN tensiunile auxiliare de faza, expresia puterii aparente complexe se poate scrie:
![]() (3.278)
(3.278)
Deoarece puterea activa P este partea reala a puterii aparente complexe, rezulta:
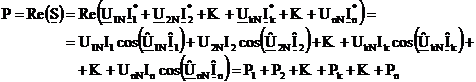 (3.279)
(3.279)
Deoarece puterea imaginara Q este partea imaginara a puterii aparente complexe rezulta:

(3.280)
Relatiile (3.279) si (3.280) se numesc expresiile cu n termeni ale puterii active respectiv reactive, intr-un circuit polifazat cu n conductoare.
OBSERVATII
1. Puterea activa P, respectiv puterea reactiva Q, totala, intr-un circuit polifazat este egala cu suma a n puteri active, respectiv, reactive monofazate date de diferentele de potential (tensiunile auxiliare de faza) U1N, U2N, , UnN intre cele n conductoare si un punct arbitrar ales, N, de potential oarecare, cu curentii de linie I1, I2, , In.
2. Puterea activa P, respectiv reactiva Q intr-un circuit polifazat cu n conductoare se poate masura prin metoda celor -n-wattmetre, respectiv, varmetre, montate ca in figura 3.84 si anume: bobinele de curent ale aparatelor se monteaza in serie pe fiecare faza, respectand polaritatea; circuitele de tensiune se conecteaza cu borna polarizata la acelasi conductor la care se afla si borna polarizata de curent, cealalta extremitate fiind legata la punctul comun N.
3. Daca P1,
P2, , Pn, respectiv Q1, Q2,, Qn
sunt indicatiile celor n wattmetre, respectiv varmetre, suma P=P1+P2+.+Pn
reprezinta puterea activa totala, iar suma Q=Q1+Q2++Qn
puterea reactiva totala. De remarcat ca unele indicatii pot
fi in sens contrar gradatiilor scarii aparatelor (pentru wattmetre
cand defazajul (![]() ) este > +
) este > + ![]() , iar pentru varmetre cand curentul Ik este
defazat inaintea tensiunii UkN, pentru citirea indicatiilor se
inverseaza legaturile la circuitul de tensiune, iar puterea se
considera cu semnul minus.
, iar pentru varmetre cand curentul Ik este
defazat inaintea tensiunii UkN, pentru citirea indicatiilor se
inverseaza legaturile la circuitul de tensiune, iar puterea se
considera cu semnul minus.

Fig.3.83 Circuit polifazat cu "n" conductoare (a) si
tensiunile auxiliare de faza U1N, U2N, , UnN (b)
4. Daca se
alege ca punct de referinta una dintre faze, rezulta ![]() , tensiunile auxiliare devenind tensiunile de linie ale circuitului:
, tensiunile auxiliare devenind tensiunile de linie ale circuitului:
![]()
Relatiile (3.279) si (3.280) devin:
![]() (3.281)
(3.281)
![]() (3.282)
(3.282)
Relatiile (3.281) si (3.282) se numesc expresiile cu n-1 termeni ai puterii active, respectiv reactive intr-un circuit polifazat cu n conductoare.
Deci, puterea
activa, respectiv reactiva, se va putea masura si prin
metoda celor n-1 wattmetre, respectiv varmetre conectate ca in figura 3.85,
renuntandu-se la aparatul de pe faza de referinta, deoarece ![]() (bobinele de curent in
serie pe fazele 1, 2, , K-l, K+l, -n, iar circuitele de tensiune se
alimenteaza cu diferentele de potential intre diversele
conductoare si faza K de referinta). Evident, exista n
variante ale metodei celor n-1 aparate, deoarece ca faza de
referinta se poate alege oricare conductor.
(bobinele de curent in
serie pe fazele 1, 2, , K-l, K+l, -n, iar circuitele de tensiune se
alimenteaza cu diferentele de potential intre diversele
conductoare si faza K de referinta). Evident, exista n
variante ale metodei celor n-1 aparate, deoarece ca faza de
referinta se poate alege oricare conductor.
5. Metodele celor n si n-1 aparate sunt valabile indiferent de gradul de nesimetrie al tensiunilor de alimentare a circuitului polifazat si de gradul de dezechilibru al curentilor de linie.
6. Numarul n-l reprezinta numarul minim de aparate care poate fi folosit pentru masurarea P si Q intr-un circuit polifazat cu -n- conductoare. Numarul n reprezinta numarul maxim de aparate care are sens sa fie utilizat.
7. In functie de punctul N ales arbitrar, puterile monofazate P1, P2, , Pn; Q1, Q2, , Qn pot sa varieze; suma lor insa ramane mereu constanta, deoarece reprezinta puterea totala activa sau reactiva absorbita de receptor.

Fig.3.84 Metoda celor "n" wattmetre (varmetre) pentru masurarea puterii active (reactive)
intr-un circuit polifazat cu "n" conductoare
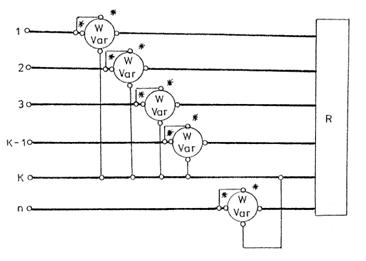
Fig.3.85 Metoda celor "n-1" wattmetre (varmetre)
8. In cazul simetriei totale a circuitului, indicatiile celor n wattmetre sau varmetre, (presupuse identice) devin egale, astfel incat poate fi pastrat un singur aparat; pentru determinarea puterii totale se multiplica indicatia acestuia cu n.
2. Masurarea puterilor active intr-un circuit trifazat fara conductor neutru
Conform teoremei generalizate, Blondel, puterea activa intr-un circuit trifazat fara conductor neutru, deci cu trei conductoare, se poate masura prin metoda celor n=3 san n-1=2 wattmetre.
Metoda celor trei wattmetre
Admitem:
a)
tensiunile de alimentare
formeaza un sistem nesimetric ![]() deci, in planul
topografic al potentialelor, triunghiul tensiunilor de linie rezulta
oarecare;
deci, in planul
topografic al potentialelor, triunghiul tensiunilor de linie rezulta
oarecare;
b)
curentii de linie
formeaza un sistem dezechilibrat ![]() ;
;
c) nu se precizeaza natura sau conexiunile receptorului.
Expresia cu n=3 termeni a teoremei generalizate Blondel pentru masurarea puterii active este:
![]() (3.283)
(3.283)
Din aceasta relatie, rezulta schema de montaj a celor trei wattmetre.
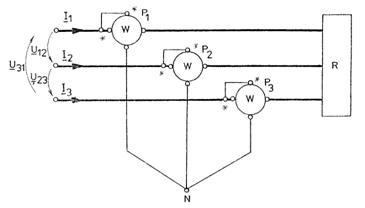
Fig.3.86 Metoda celor trei wattmetre pentru masurarea puterii active
in circuite trifazate
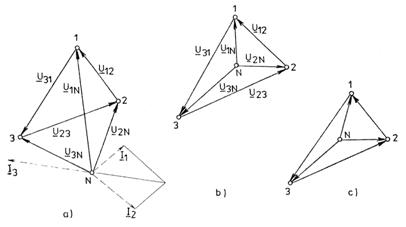
Fig.3.87 Diagrame fazoriale ale circuitului din figura 3.86
Punctul N poate ocupa in planul topografic al potentialelor, urmatoarele pozitii:
a) in exteriorul triunghiului tensiunilor de linie, daca N primeste artificial din exterior un anumit potential (figura 3.87 a);
b)
in interiorul triunghiului, intr-o
pozitie oarecare in functie de rezistentele circuitelor de
tensiune ale wattmetrelor, daca ![]() (fig.3.87 b) daca
N este lasat liber;
(fig.3.87 b) daca
N este lasat liber;
c)
in centrul de greutate al
triunghiului, N=G, daca circuitele de tensiune ale wattmetrelor au
rezistentele egale ![]() (fig.3.87 c)
(fig.3.87 c)
OBSERVATIE:
Valoarea maxima a tensiunilor U1N, U2N, U3N care se aplica circuitelor de tensiune ale celor trei wattmetre poate fi tensiunea de linie a circuitului trifazat (se vor alege deci corespunzator domeniile de masurare ale wattmetrelor).
Metoda unui singur watttmetru
Admitem:
a)
tensiunile de alimentare
formeaza un singur sistem simetric ![]() , deci in planul topografic al potentialelor, triunghiul
tensiunilor de linie este echilibrat (fig.3.88);
, deci in planul topografic al potentialelor, triunghiul
tensiunilor de linie este echilibrat (fig.3.88);
b)
curentii de linie
formeaza un sistem echilibrat ![]() ;
;
c)
deoarece punctul comun al
circuitelor de tensiune, aplicand metoda celor trei wattmetre, rezulta in
centrul de greutate al triunghiului, tensiunile auxiliare de faza U1N,
U2N, U3N se confunda cu tensiunile stelate ale
distributiei trifazate simetrice E1, E2, E3.
Tensiunile stelate formeaza un sistem simetric ![]() ;
;
d) defazajele dintre tensiunile stelate de faza si curentii de linie sunt egale:
![]()
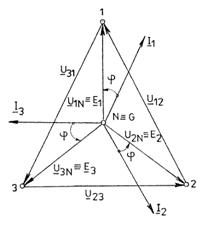
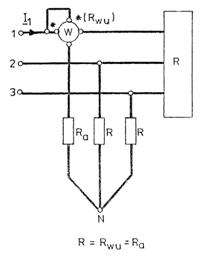
Fig.3.88 Diagrama fazoriala pentru: Fig.3.89 Metoda unui singur wattmetru
a) U12=U23=U31=U; pentru masurarea puterii active
b) I1=I2=I3=I.
In conditiile admise, puterile indicate de cele trei wattmetre (aplicand metoda celor trei wattmetre) sunt egale si relatia:
![]()
devine:
![]() (3.284)
(3.284)
Deci, puterea activa trifazata poate fi masurata cu un singur wattmetru cu conditia de a se conserva ansamblul celor trei rezistente egale, in scopul crearii unui punct neutru artificial N, situat in centrul de greutate al triunghiului.
Rezulta montajul unui singur wattmetru (fig.3.89) in care Rwu este rezistenta circuitului sau de tensiune, iar Ra, R=Ra + Rwu si R=Ra +Rwu sunt trei rezistente aditionale pentru crearea punctului neutru N. Daca P1, este indicatia acestui wattmetru, puterea activa trifazata va fi:
![]() (3.285)
(3.285)
OBSERVATII:
1. Metoda unui singur wattmetru nu se aplica la masurarea puterii microreceptoarelor (prezenta aparatului pe una din faze produce o nesimetrie a sistemului de tensiuni aplicat receptorului).
2. Daca punctul neutru al receptorului este accesibil (sarcina simetrica montata in stea) wattmetrul poate fi conectat cu borna nepolarizata la acest punct neutru, rezistentele auxiliare nemaifiind necesare (fig.3.90).
3. Masurarea puterii cu wattmetrul montat indirect, prin intermediul transformatoarelor de masura, se realizeaza conform schemei din fig.3.91.
4. Wattmetrele monofazate montate permanent (de tablou) in circuitele trifazate echilibrate dupa schemele din figurile 3.90 si 3.91 au de obicei scara gradata astfel incat sa indice direct puterea activa trifazata.
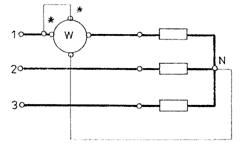
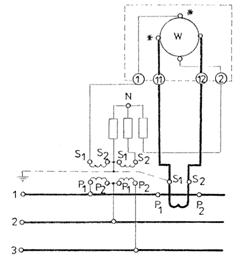
Fig.3.90 Montajul wattmetruluipentru Fig.3.91 Montajul indirect al unui wattmetru
receptor cu nulul accesibil pentru masurarea puterii intr-un
circuit trifazat
Metoda celor doua wattmetre
Admitem:
a)
tensiunile de alimentare
formeaza un sistem nesimetric ![]() (triunghiul
tensiunilor de linie este oarecare);
(triunghiul
tensiunilor de linie este oarecare);
b)
curentii de linie
formeaza un sistem dezechilibrat ![]() ;
;
c) se adopta faza 2 ca referinta, deci N=2.
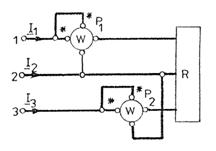
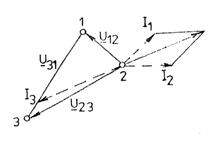
Fig.3.92 Metoda celor doua weattmetre Fig.3.93 Diagrama fazoriala pentru:
a) U12 U23 U31;
b) I1 I2 I3.
In aceste conditii tensiunile auxiliare devin:
![]() (3.286)
(3.286)
Teorema lui Blondel (expresia n-l=2 termeni) devine:
![]() (3.287)
(3.287)
Corespunzator rezulta schema de montare a celor doua wattmetre (fig.3.92) si diagrama fazoriala a circuitului (fig.3.93).
In cazul particular al unui circuit cu tensiuni simetrice si curenti echilibrati sunt indeplinite conditiile:
![]()
Din diagrama
fazoriala din figura 3.94 rezulta ca defazajul dintre ![]() si
si ![]() este de
este de ![]() iar defazajul dintre
iar defazajul dintre ![]() si
si ![]() este
este ![]() , deci puterile
masurate de cele doua wattmetre rezulta:
, deci puterile
masurate de cele doua wattmetre rezulta:
![]() (3.288)
(3.288)
![]() (3.289)
(3.289)

Fig.3.94 Diagrama fazoriala pentru:
a) U12=U23=U;
b) I1=I2=I3=I.
OBSERVATII:
1. Pentru un
receptor capacitiv in expresiile puterilor P1 si P2
se modifica semnul defazajului ![]() .
.
2. Pe baza
indicatiilor celor doua wattmetre se poate obtine defazajul ![]() , cu relatia:
, cu relatia:
![]() (3.290)
(3.290)
3. Pentru receptor
pur rezistiv, indicatiile celor doua wattmetre sunt egale (P1=P2)
cand ![]() . Pentru un receptor pur reactiv
. Pentru un receptor pur reactiv ![]() puterile masurate
de cele doua wattmetre sunt egale si de semn contrar (-P1=P2),
deci puterea activa totala (trifazata) este nula. Pentru
puterile masurate
de cele doua wattmetre sunt egale si de semn contrar (-P1=P2),
deci puterea activa totala (trifazata) este nula. Pentru ![]() , P1=0, deci P=P2.
, P1=0, deci P=P2.
4. Din indicatiile celor doua wattmetre, se poate deduce si puterea reactiva trifazata:
![]() (3.291)
(3.291)
5. In scopul masurarii puterii active trifazate cu un singur aparat, s-au construit wattmetre trifazate denumite si wattmetre duble. Wattmetrele duble de tip electrodinamic sunt compuse din doua wattmetre monofazate, avand bobinele de tensiune cuplate pe acelasi ax (asupra caruia actioneaza astfel suma cuplurilor date de cele doua wattmetre) care sunt conectate in circuitul trifazat dupa schema din figura 3.95.
Masurarea puterii trifazate cu ajutorul wattmetrelor duble putandu-se aplica atat in cazul circuitelor cu tensiuni simetrice si curenti echilibrati, cat si in cazul circuitelor cu tensiuni nesimetrice si curenti dezechilibrati, are o mare raspandire in practica. Scara wattmetrelor duble este adeseori gradata direct in wati, puterea maxima marcata pe cadran fiind egala cu P=1,73 UnIn (unde Un si In sunt valorile nominale pentru care este construit wattmetrul).
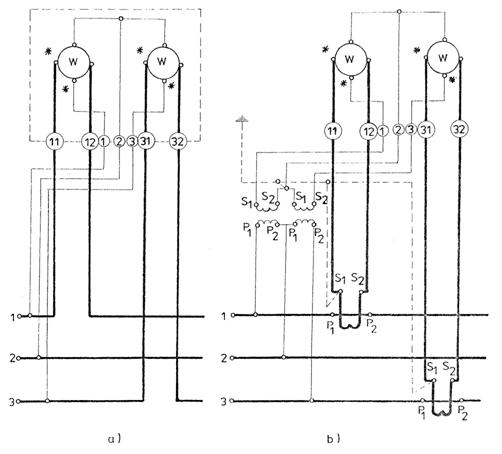
Fig.3.95 Wattmetrul trifazat (dublu)
a) montaj direct;
b) montaj indirect.
3. Masurarea puterii active intr-un circuit trifazat cu conductor neutru
Conform teoremei lui Blondel pentru masurarea puterii active se pot adopta metodele celor patru si trei wattmetre (la care se alege ca faza de referinta conductorul neutru). Expresia cu n=4 termeni a teoremei lui Blondel rezulta:
![]() (3.292)
(3.292)
Din relatia de mai sus rezulta modul de conectare a celor patru wattmetre (fig.3.96) si diagrama fazoriala din fig.3.97.
Expresia cu n-1=3 termeni a teoremei lui Blondel rezulta:
![]() (3.293)
(3.293)
Rezulta deci modul de conectare a celor trei wattmetre (figura 3.98) si diagramele fazoriale corespunzand cazului prezentei, respectiv absentei impedantei pe conductorul neutru (fig.3.99 si 3.100).
Receptorul, in cazul acestor circuite, este de regula montat in stea si nu contine impedanta pe conductorul neutru, astfel incat cele trei wattmetre din fig.3.98 masoara fiecare puterea consumata pe faza respectiva. Puterea totala a circuitului este data de suma indicatiilor celor trei wattmetre:
![]() (3.294)
(3.294)

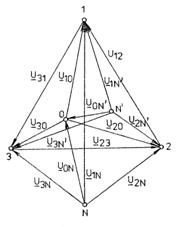
Fig.3.96 Metoda celor patru wattmetre Fig.3.97 Diagrama fazoriala a schemei
din figura 3.96



Fig.3.98 Metoda celor trei Fig.3.99 Diagrama fazoriala Fig.3.100 Diagrama fazoriala
wattmetre in cazul unei impedante in cazul absentei impedantei
pe conductorul neutru pe conductorul neutru
Indicatiile wattmetrelor sunt intotdeauna pozitive, oricare ar fi dezechilibrul curentilor, nesimetria tensiunilor si caracterul sarcinii.
In scopul masurarii directe a puterii active trifazate data de expresia (3.294), se folosesc wattmetre trifazate cu cate trei sisteme active, avand bobinele de tensiune fixate pe un ax comun care, fiind actionat de toate cele trei cupluri active, produce deviatie proportionala cu puterea totala consumata in circuit (figura 3.101)
In cazul particular al sistemului simetric de tensiuni si sistemului echilibrat de curenti, se poate utiliza metoda unui singur wattmetru (fig.3.102).

Fig.3.101 Wattmetru trifazat cu trei sisteme active
(montaj semiindirect, cu transformatoare de curent si rezistente aditionale)
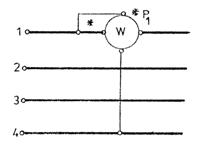
Fig.3.102 Metoda unui singur wattmetru pentru masurarea puterii
intr-un circuit trufazat cu conductor neutru
4. Masurarea puterii reactive in circuite trifazate fara conductor neutru
Metoda celor trei wattmetre in montaj special, alimentate cu tensiuni auxiliare de faza
Admitem:
a)
tensiunile de linie care
alimenteaza circuitul trifazat formeaza un sistem simetric, ![]() (deci triunghiul reprezentativ
al fazorilor rezulta echilibrat);
(deci triunghiul reprezentativ
al fazorilor rezulta echilibrat);
b)
curentii de linie
formeaza un sistem dezechilibrat ![]() ;
;
c) nu se fac precizari asupra naturii si conexiunilor receptorului.
Din teoria lui Blondel rezulta:
![]() (3.295)
(3.295)
In conformitate cu
metoda de masurare directa a puterii reactive cu wattmetrul in montaj
special, alimentat cu o tensiune auxiliara, se vor determina puterile
active ![]() echivalente puterilor
reactive Q1, Q2 si Q3. Din diagrama
fazoriala urmeaza sa se gaseasca tensiunile auxiliare
echivalente puterilor
reactive Q1, Q2 si Q3. Din diagrama
fazoriala urmeaza sa se gaseasca tensiunile auxiliare ![]() si
si ![]() care sa fie
defazate cu
care sa fie
defazate cu ![]() in urma
fata de tensiunile de baza
in urma
fata de tensiunile de baza ![]() si
si ![]() . Dar
. Dar ![]() , punctul N fiind ales chiar in centrul de greutate al
triunghiului echilateral. Tensiunile stelate de faza, E1, E2
si E3 formeaza un sistem simetric, deci
, punctul N fiind ales chiar in centrul de greutate al
triunghiului echilateral. Tensiunile stelate de faza, E1, E2
si E3 formeaza un sistem simetric, deci ![]() . Din diagrama fazoriala se determina tensiunea
. Din diagrama fazoriala se determina tensiunea ![]() defazata cu
defazata cu ![]() in urma
fata de
in urma
fata de ![]() ; aceasta este U23. Deci puterea
reactiva monofazata Q1 (conform relatiei
; aceasta este U23. Deci puterea
reactiva monofazata Q1 (conform relatiei ![]() ) rezulta:
) rezulta:
![]() (3.296)
(3.296)
in care
![]() (3.297)
(3.297)
deci
![]() (3.298)
(3.298)
Analog se determina
tensiunile U31 si U12 fiind defazate
cu ![]() in urma
fata de
in urma
fata de ![]() si
si ![]() ; rapoartele
; rapoartele ![]() si
si ![]() avand aceeasi
valoare
avand aceeasi
valoare ![]() rezulta:
rezulta:
![]() (3.299)
(3.299)
![]()
Puterea reactiva trifazata totala va fi data de relatia:
![]() (3.300)
(3.300)

Fig.3.103 Diagrama fazoriala pentru:
a) U12=U23=U31;
b) I1 I2 I3.
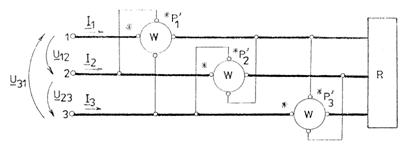
Fig.3.104 Metoda celor trei wattmetre pentru masurarea puterilor reactive
in circuite trifazate fara conductor neutru
Deci, bobinele de curent ale wattmetrelor se monteaza in serie pe cele trei faze ale circuitului; circuitele de tensiune ale wattmetrelor se alimenteaza cu tensiunile intre fazele urmatoare celei pe care se monteaza bobina de curent (fig.3.104).
Metoda unui singur wattmetru pentru masurarea puterii reactive
(caz particular al metodei precedente)
Admitem:
a)
tensiunile de linie formeaza
un sistem simetric ![]() ;
;
b)
curentii de linie
formeaza un sistem echilibrat ![]() .
.
Circuitul trifazat este deci cu simetrie totala (de tensiune si curent).
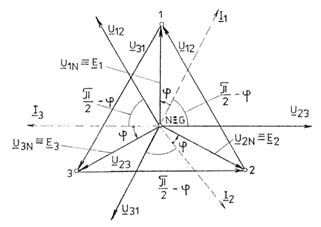
Fig.3.105 Diagrama fazoriala pentru:
a) U12=U23=U31=U;
b) I1=I2=I3=I.
Din diagrama
fazoriala se observa ca puterile ![]() cu expresiile:
cu expresiile:
![]() ;
; ![]() ;
;
![]() (3.301)
(3.301)
Deci puterea reactiva trifazata totala este:
![]() (3.302)
(3.302)
Deoarece puterile ![]() sunt egale, puterea
reactiva trifazata se poate masura cu ajutorul unui singur wattmetru,
montat ca in figura 3.106 (de exemplu) cu bobina de curent pe faza intai, iar
circuitul de tensiune conectat intre fazele 2 si 3. Puterea reactiva
totala Q este egala cu puterea activa indicata de
wattmetru,
sunt egale, puterea
reactiva trifazata se poate masura cu ajutorul unui singur wattmetru,
montat ca in figura 3.106 (de exemplu) cu bobina de curent pe faza intai, iar
circuitul de tensiune conectat intre fazele 2 si 3. Puterea reactiva
totala Q este egala cu puterea activa indicata de
wattmetru, ![]() , multiplicata cu
, multiplicata cu ![]() .
.
![]()

Fig.3.106 Metoda unui singur wattmetru pentru masurarea puterii reactive
Metoda celor doua wattmetre in montaj special, alimentate cu tensiuni auxiliare
de faza
Admitem:
a)
tensiunile de linie formeaza
un sistem simetric ![]() ;
;
b)
curentii de linie
formeaza un sistem dezechilibrat ![]() .
.
Din teorema lui Blondel, expresia cu doi termeni, deducem
![]() (3.303)
(3.303)

![]()
Fig.3.107 Diagrama fazoriala pentru determinarea tensiunilor de faza
Din diagrama
fazoriala (fig. 3.107) rezulta ca tensiunea defazata cu ![]() in urma
fata de U12 este
in urma
fata de U12 este ![]() , iar tensiunea defazata cu
, iar tensiunea defazata cu ![]() in urma
fata de U32 este
in urma
fata de U32 este ![]() . Deoarece tensiunile stelate de faza formeaza un
sistem simetric
. Deoarece tensiunile stelate de faza formeaza un
sistem simetric ![]() rezulta ca
raportul dintre tensiunea de baza U si tensiunea auxiliara de
faza E este acelasi pentru ambele wattmetre, deci:
rezulta ca
raportul dintre tensiunea de baza U si tensiunea auxiliara de
faza E este acelasi pentru ambele wattmetre, deci: ![]() . Puterea reactiva este:
. Puterea reactiva este:
![]() (3.304)
(3.304)
Puterea reactiva poate fi masurata cu doua wattmetre montate ca in fig.3.108.

![]()
Fig.3.108 Metoda celor doua wattmetre pentru masurarea puterii reactive trifazate
In schema din fig.3.108 tensiunile E1 si E3 se obtin prin crearea punctului neutru artificial N cu ajutorul rezistentei R de valoare egala cu rezistentele circuitelor de tensiune ale celor doua wattmetre.
In cazul particular
al sistemului echilibrat de curenti ![]() pe baza diagramei
fazoriale din fig.3.109 se deduc expresiile puterilor active masurate de
cele doua wattmetre.
pe baza diagramei
fazoriale din fig.3.109 se deduc expresiile puterilor active masurate de
cele doua wattmetre.
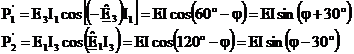 (3.305)
(3.305)
Pe baza
indicatiilor ![]() si
si ![]() ale wattmetrelor se
pot determina:
ale wattmetrelor se
pot determina:
a)
puterea reactiva: ![]() (3.306)
(3.306)
b)
puterea activa: ![]() (3.307)
(3.307)
c)
defazajul receptorului: ![]() (3.308)
(3.308)
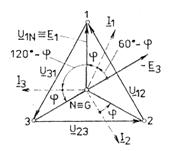
Fig.3.109 Diagrama fazoriala pentru:
a) U12=U23=U31=U;
b) I1=I2=I3=I.
5. Masurarea puterii reactive in circuite trifazate cu conductor neutru
In circuitele trifazate cu conductor neutru, alimentate cu tensiuni simetrice se foloseste schema cu n-l=3 wattmetre, in montaj special, alimentate cu tensiuni auxiliare. Expresia cu trei termeni a teoremei Blondel este (adoptand conductorul neutru ca faza de referinta):
![]() (3.309)
(3.309)
Din diagrama
fazoriala se deduc tensiunile cu care se alimenteaza wattmetrele ![]() rezultand schema de
montaj din figura 3.111.
rezultand schema de
montaj din figura 3.111.
Expresia puterii reactive trifazate totale este:
![]() (3.310)
(3.310)
In cazul particular al tensiunilor simetrice si curentilor echilibrati, puterea reactiva se poate masura cu un singur wattmetru (fig.3.112).
Expresia puterii reactive trifazate totale, in acest caz, este
![]() (3.311)
(3.311)
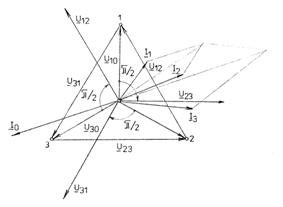
![]()
Fig.3.110 Diagrama fazoriala pentru circuit trifazat cu conductor neutru
RECEPTOR

![]()
Fig.3.111 Metoda celor trei wattmetre pentru masurarea puterii reactive
intr-un circuit trifazat cu conductor neutru
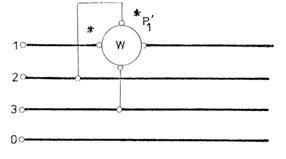
![]()
Fig.3.112 Metoda unui singur wattmetru pentru masurarea puterii reactive
intr-un circuit trifazat cu conductor neutru
|
Politica de confidentialitate |
| Copyright ©
2025 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |