
Modulatia in invertoarele trifazate
1. Modulatia in unda rectangulara
Un invertor trifazat de tensiune se realizeaza dupa schema din figura 1
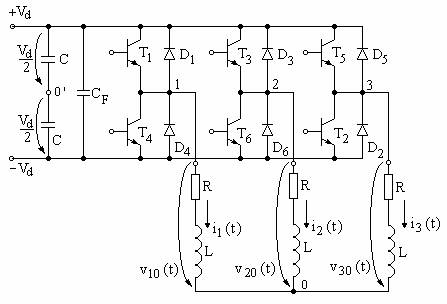
Fig. 1 Invertor de tensiune trifazat.
Invertorul
trifazat este format din trei brate identice de invertor monofazat in
semipunte. Sarcina, de tipul R+L, este trifazata, simetrica si
conectata in stea, putand fi o masina trifazata de c.a. Este
notat prin 0 nodul sarcinii, iar prin 0' punctul median al sursei de alimentare
![]() , punct de calcul.
, punct de calcul.
Modulatia in unda rectangulara presupune, figura 14:
comanda comutatoarelor statice de
pe un brat, in antifaza, pe un interval ![]() , unde T este perioada de comanda;
, unde T este perioada de comanda;
comanda pe cele trei brate
este decalata cu ![]() .
.
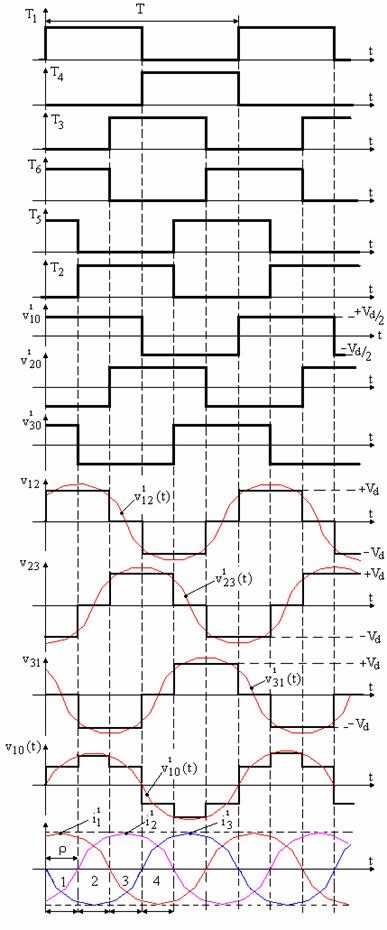
Fig. 14. Modulatia in unda dreptunghiulara pentru invertoare trifazate
Numerotarea
comutatoarelor statice, figura 14, se face in ordinea intrarii in
conductie. In functie de starea comutatoarelor statice, in figura 14 sunt calculate si reprezentate
tensiunile ![]() ,
, ![]() si
si ![]() realizate de cele trei
brate. Tensiunile de linie sunt calculate cu relatii de forma:
realizate de cele trei
brate. Tensiunile de linie sunt calculate cu relatii de forma:
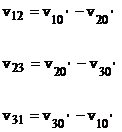 (42)
(42)
care sunt de asemenea reprezentate in figura 14. Acestea sunt de forma tensiunii de iesire a unui invertor in punte monofazat comandat in unda quasirectangulara la:
![]() ; (43)
; (43)
Aceasta inseamna ca valoarea de varf a tensiunii de linie este:
![]() (44)
(44)
iar valoarea efectiva:
![]() (45)
(45)
Se
remarca de asemenea faptul ca tensiunilor de linie li se poate regla
frecventa prin intermediul perioadei de comanda T, dar au valoarea
efectiva constanta. Aceasta se poate modifica numai prin alimentare
cu o tensiune ![]() reglabila, deci
de la un redresor comandat.
reglabila, deci
de la un redresor comandat.
Pentru
calculul tensiunilor de faza, tensiunile ![]() ,
, ![]() si
si ![]() , se aplica teorema a doua a lui Kirchhoff pentru fiecare
brat dupa:
, se aplica teorema a doua a lui Kirchhoff pentru fiecare
brat dupa:
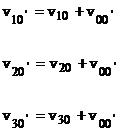 (46)
(46)
Se aduna relatiile (46) de unde rezulta:
![]() (47)
(47)
intrucat: ![]() (48)
(48)
ca urmare a faptului ca receptorul trifazat este simetric. Din (46) si (47) se determina cele trei tensiuni de faza dupa:
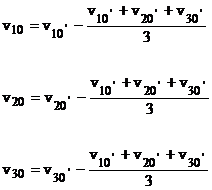 (49)
(49)
In figura 14 este
reprezentata o singura tensiune de faza, ![]() , ea avand o variatie in doua trepte,
, ea avand o variatie in doua trepte, ![]() si
si ![]() .
.
Atat
tensiunile de linie cat si cele de faza au armonica fundamentala
de perioada T. Se constata ca fundamentala celor trei tensiunii
de linie, ![]() ,
, ![]() si
si ![]() , alcatuiesc un sistem trifazat de simetric de
succesiune directa, valorile de varf efective fiind date de relatiile
(44) si respectiv (45). Fundamentala tensiunilor de faza,
, alcatuiesc un sistem trifazat de simetric de
succesiune directa, valorile de varf efective fiind date de relatiile
(44) si respectiv (45). Fundamentala tensiunilor de faza, ![]() ,
, ![]() si
si ![]() alcatuiesc de
asemenea un sistem trifazat simetric de succesiune directa, defazat in
urma celui de linie cu
alcatuiesc de
asemenea un sistem trifazat simetric de succesiune directa, defazat in
urma celui de linie cu ![]() . In concluzie, iesirea, la nivelul fundamentalelor, reprezinta un
sistem trifazat in acceptiunea obisnuita.
. In concluzie, iesirea, la nivelul fundamentalelor, reprezinta un
sistem trifazat in acceptiunea obisnuita.
Continutul de armonici.
La prima vedere, forma tensiunilor de linie fiind aceeasi ca la modulatia in unda quasirectangulara, continutul de armonici este cel caracteristic acestui tip de modulatie, adica intreg spectru de armonici impare:
![]() , (50)
, (50)
unde k este un numar intreg.
In
realitate, ca urmare a comenzii decalate pe cele trei brate cu ![]() , adica cu
, adica cu ![]() , armonicile multiplu de trei ale tensiunilor
, armonicile multiplu de trei ale tensiunilor ![]() ,
, ![]() si
si ![]() , sunt in faza. Ca urmare a relatiilor de calcul (42),
aceste armonici se anuleaza, spectrul fiind de forma:
, sunt in faza. Ca urmare a relatiilor de calcul (42),
aceste armonici se anuleaza, spectrul fiind de forma:
![]() (51)
(51)
adica armonicile 5, 7, 11, 13, s. a.
m. d. Asadar spectrul de armonici al tensiunilor de linie este mult mai
favorabil decat la ondulorul monofazat cu comanda similara. In ceea
ce priveste tensiunile de faza ![]() ,
, ![]() si
si ![]() , continutul de armonici este cel identic cu cel al
tensiunilor de linie, amplitudinea acestora fiind mai redusa ca urmare a
variatiei in treptele
, continutul de armonici este cel identic cu cel al
tensiunilor de linie, amplitudinea acestora fiind mai redusa ca urmare a
variatiei in treptele ![]() si
si ![]() .
.
Curentii
de faza ![]() ,
, ![]() si
si ![]() se pot determina in
acelasi mod ca la cazul monofazat. Continutul lor de armonici va fi
considerabil diminuat ca urmare a sarcinii de tip R+L. in figura 14 sunt reprezentate numai fundamentalele
se pot determina in
acelasi mod ca la cazul monofazat. Continutul lor de armonici va fi
considerabil diminuat ca urmare a sarcinii de tip R+L. in figura 14 sunt reprezentate numai fundamentalele ![]() ,
, ![]() si
si ![]() ale curentilor de
faza, decalati cu j in urma
tensiunilor de faza corespunzatoare.
ale curentilor de
faza, decalati cu j in urma
tensiunilor de faza corespunzatoare.
Conductia in invertor.
In invertoarele trifazate, conductia este mult mai complicata decat la cele monofazate ca urmare a circulatiei trifazate a curentului. Pentru a analiza modul de inchidere a curentilor se considera intervalele de la 1 la 4 din figura 14. Delimitarea intervalelor de mai sus se face fie de la schimbarea semnului unui curent, fie de la modificarea comenzii. Conductia decurge dupa:
|
|
a) Intervalul 1, fig. 15: sunt comandate curentii au sensurile: conduc comutatoarele statice: b) Intervalul 2, fig. 16: sunt comandate curentii au sensurile: conduc comutatoarele statice: c) Intervalul 3, fig. 17: sunt comandate curentii au sensurile: conduc comutatoarele statice: d) Intervalul 4, fig. 18: sunt comandate curentii au sensurile: conduc comutatoarele statice: Analiza conductiei pe cele patru intervale conduce la concluziile urmatoare: participa la conductie fie comutatoarele statice, fie diodele antiparalel, acestea in functie de comanda si in sensul curentului; conductia este in permanenta neintrerupta, ca urmare a existentei cailor de inchidere, indiferent de structura lor, la un moment dat, a starii comutatoarelor statice si/sau diodelor. Pe de alta parte, daca scriem teorema a doua a lui Kirchhoff in nodul 0, pentru figura 15, rezulta: Dar de la sursa este absorbit numai curentul ceea ce inseamna ca |
|
Fig. 15. Conductia pe intervalul 1 |
|
|
|
|
|
Fig. 16. Conductia pe intervalul 2 |
|
|
|
|
|
Fig. 17. Conductia pe intervalul 3 |
|
|
|
|
|
Fig. 18. Conductia pe intervalul 4 |
Comanda PWM pentru invertoare trifazate
PWM pentru invertoare trifazate se va analiza pentru convertorul de tensiune din figura 1 Cele trei brate ale ondulorului se comanda cu trei tensiuni de forma:
![]()
![]() (54)
(54)
![]()
unde ![]() (55)
(55)
T fiind perioada de comanda, fig. 19.
Logica
de comanda rezulta, pentru fiecare brat, dupa modelul de la
PWM unipolar. In fig. 19, din motive de complexitate a desenului, este
reprezentata numai determinarea tensiunilor ![]() si
si ![]() si a tensiunilor
de linie:
si a tensiunilor
de linie:
![]() (56)
(56)
Fundamentala tensiunii ![]() ,
, ![]() , rezulta, in acelasi mod ca la modulatia in
unda rectangulara, defazata cu
, rezulta, in acelasi mod ca la modulatia in
unda rectangulara, defazata cu ![]() inaintea tensiunii de
comanda
inaintea tensiunii de
comanda ![]() . Determinarea tensiunilor
. Determinarea tensiunilor ![]() si
si ![]() se face in
acelasi mod, rezultand tot un sistem trifazat simetric de succesiune
directa.
se face in
acelasi mod, rezultand tot un sistem trifazat simetric de succesiune
directa.
Tensiunile
de faza ![]() ,
, ![]() si
si ![]() se calculeaza cu
relatiile (49) rezultand pulsuri de latime variabila
si cu amplitudini in doua trepte.
se calculeaza cu
relatiile (49) rezultand pulsuri de latime variabila
si cu amplitudini in doua trepte.
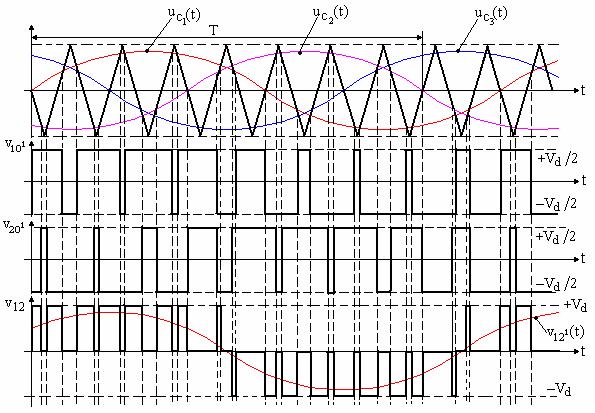
Fig. 19. MLI trifazat
Calculul tensiunilor de iesire.
Fiecare
brat al invertorului este un invertor in semipunte, fig. 1 Valoarea de
varf a tensiunii ![]() , in cazul modulatiei liniare,
, in cazul modulatiei liniare, ![]() , va fi:
, va fi:
![]() , (57)
, (57)
iar valoarea efectiva: 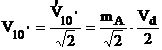 (58)
(58)
Ca
urmare a comenzii trifazate pe cele trei brate, valoarea efectiva a
tensiunilor de linie va fi: ![]() , (59)
, (59)
Cazul
modulatiei neliniare, ![]() , se analizeaza la fel ca la ondulorul monofazat avand
aceleasi particularitati. Valoarea maxima a tensiunii de
linie este cea caracteristica modulatiei in unda
rectangulara, ecuatia (45).
, se analizeaza la fel ca la ondulorul monofazat avand
aceleasi particularitati. Valoarea maxima a tensiunii de
linie este cea caracteristica modulatiei in unda
rectangulara, ecuatia (45).
Valoarea efectiva a tensiunilor de faza pe sarcina conectata in stea se obtine din (59) prin relatia de legatura:
![]() (60)
(60)
Continutul de armonici
Tensiunile
![]() ,
, ![]() si
si ![]() contin spectrul
de armonici caracteristic PWM bipolar. Datorita comenzii decalate cu
contin spectrul
de armonici caracteristic PWM bipolar. Datorita comenzii decalate cu ![]() pe cele trei
brate, la fel ca la PWM unipolar, armonicile multiplu de trei se
anuleaza din tensiunile de linie, ca urmare a faptului ca defazajul
dintre ele este:
pe cele trei
brate, la fel ca la PWM unipolar, armonicile multiplu de trei se
anuleaza din tensiunile de linie, ca urmare a faptului ca defazajul
dintre ele este:
![]() (61)
(61)
Ca urmare, prin alegerea unei modulatii in frecventa:
![]() , (62)
, (62)
spectrul de armonici se poate diminua
considerabil. Astfel, in tabelul 2 sunt prezentate, pentru un astfel de caz,
valorile efective ale fundamentalei si principalelor armonici raportate la
tensiunea de alimentare ![]() . Se constata o diminuare a continutului de
armonici fata de cazul monofazat. In cazul modulatiei neliniare
apar toate armonicile impare, mai putin cele multiplu de trei.
. Se constata o diminuare a continutului de
armonici fata de cazul monofazat. In cazul modulatiei neliniare
apar toate armonicile impare, mai putin cele multiplu de trei.
Tabelul 2
|
h | |||||
|
|
|||||
|
| |||||
|
| |||||
|
|
Modulatia fazoriala
Un sistem trifazat simetric de tensiuni se poate scrie sub forma:
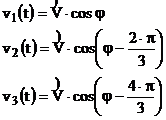 (65)
(65)
fiind in fapt definit prin doua
marimi; valoarea maxima ![]() si faza
initiala j
si faza
initiala j
Se ataseaza sistemului trifazat un numar complex, numit fazor spatial,
![]()
![]() , (66)
, (66)
unde: ![]() (67)
(67)
Dezvoltand (66) rezulta:
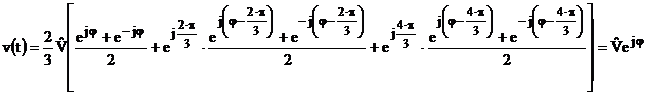 (68)
(68)
Pe
de alta parte un ondulor trifazat cu modulatie in unda
dreptunghiulara realizeaza un sistem de tensiuni, care se
modifica la fiecare interval ![]() , ca urmare a
modificarii starii comutatoarelor statice. In tabelul 3 sunt
calculate tensiunile rezultante si fazorul spatial pentru cele 6
secvente diferite pe o perioada. Calculele sunt efectuate pentru
tensiunile oferite de bratele ondulorului din fig. 13 si formele
, ca urmare a
modificarii starii comutatoarelor statice. In tabelul 3 sunt
calculate tensiunile rezultante si fazorul spatial pentru cele 6
secvente diferite pe o perioada. Calculele sunt efectuate pentru
tensiunile oferite de bratele ondulorului din fig. 13 si formele ![]() ,
, ![]() si
si ![]() din fig. 14.
din fig. 14.
Tabelul 3
|
Secventa |
CS comandate |
Tensiuni |
Fazor spatial |
||||
|
|
|
|
|||||
|
T1 |
T6 |
T2 |
|
|
|
|
|
|
T1 |
T3 |
T2 |
|
|
|
|
|
|
T4 |
T3 |
T2 |
|
|
|
|
|
|
T4 |
T3 |
T5 |
|
|
|
|
|
|
T4 |
T6 |
T5 |
|
|
|
|
|
|
T1 |
T6 |
T5 |
|
|
|
|
|
Daca se reprezinta in planul complex cei 6 fazori spatiali obtinuti rezulta desenul din fig. 20, in paranteze fiind notate comutatoarele statice comandate. Se mai poate obtine si al saptelea fazor spatial:
![]() (69)
(69)
|
|
pentru cazul in care sunt comandate simultan fie CS1, CS3 si CS5, fie CS2, CS4 si CS6. Cu alte cuvinte,
utilizand toate combinatiile posibile ale starilor celor 6
comutatoare statice, nu se pot obtine decat 7 fazori spatiali
precis determinati. Pentru aplicatiile din domeniul
actionarilor electrice este necesar un sistem trifazat de tensiuni
continue reglabile in frecventa si amplitudine, adica
marimile |
|
Fig. 20. Fazorii spatiali |
In acest sens, in fig. 21 este prezentata posibilitatea de realizare a fazorului:
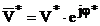 (70)
(70)
aflat in cadranul I.
|
|
Pe de alta parte nu se poate realiza o
deplasare continua a fazorului unde: fc fiind frecventa de comutatie. |
|
Fig. 21. Realizarea fazorului |
Aproximarea
fazorului ![]() se realizeaza
prin durate de realizare diferite ale fazorilor
se realizeaza
prin durate de realizare diferite ale fazorilor ![]() ,
, ![]() si
si ![]() , astfel incat sa se obtina fazorul impus. In
aceste conditii se poate scrie:
, astfel incat sa se obtina fazorul impus. In
aceste conditii se poate scrie:
![]() (73)
(73)
respectiv:
![]() (74)
(74)
unde t1, t2 si t0
sunt duratele de realizare a fazorilor ![]() ,
, ![]() si
si ![]() pe o perioada de
esantionare
pe o perioada de
esantionare ![]() . Calculul duratelor de mai sus se face din triunghiul ABC
dupa:
. Calculul duratelor de mai sus se face din triunghiul ABC
dupa:
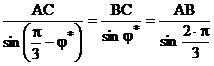 (75)
(75)
Dar:
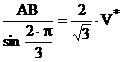 (76)
(76)
Pe de alta parte:
![]() (77)
(77)
iar:
![]() (78)
(78)
si:
![]() (79)
(79)
Din (75), (76), (78), si (79) se obtine:
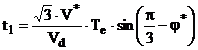 (80)
(80)
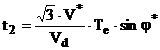 (81)
(81)
![]() (82)
(82)
|
|
Considerandu-se o comanda simetrica a comutatoarelor statice rezulta diagrama de comanda din fig. 22, unde t , timpul de comanda al comutatorului static T1 are valoarea:
pentru T3:
si pentru T5:
Comutatoarele statice |
|
Politica de confidentialitate |
| Copyright ©
2026 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |