Rationamentul aproximativ utilizeaza cu preponderenta doua reguli de inferenta: compozitionala si modus ponens generalizat. Prima regula utilizeaza o relatie fuzzy pentru reprezentarea explicita a conexiunii intre doua propozitii fuzzy, pe cand cea de-a doua utilizeaza enunturi fuzzy "daca - atunci".
Daca S1 si S2 sunt nume simbolice de obiecte, iar P1, P2, Q1, Q2 sunt proprietati ale acestor obiecte, schema simbolica de inferenta pentru ponens generalizat este:
"S1 este Q1; daca S1 este P1 atunci S2 este P2; S2 este este Q2" (3.45)
Regula compozitionala poate fi considerata ca un caz particular al celei de mai sus. Daca R este o relatie intre S1 si S2, inferenta compozitionala are forma:
"S1 este Q1; S1RS2; S2 este Q2" (3.46)
Reprezentarea semnificatiei unei reguli de tip " daca X este A atunci Y este B" se
face prin relatii derivate din logica
multivalenta, initiata de Lukasiewicz si
dezvoltata de Rescher sau Bolc. Logica cu valori infinite ![]() propune doua moduri pentru determinarea
valorii de adevar a aplicatiei
propune doua moduri pentru determinarea
valorii de adevar a aplicatiei ![]()
![]() (3.47)
(3.47)
Semnificatia regulii fuzzy "daca A atunci B" poate fi considerata a fi aceeasi cu a propozitiei compuse fuzzy "non A sau B". Pentru ca operatia sau se executa cu operatorul de intersectie, este nevoie de extensiile lui non A si B. Se obtine astfel o prima relatie care reprezinta implicatia fuzzy:
![]() (3.48)
(3.48)
Pentru reprezentarea implicatiilor, logica fuzzy preia mai multe relatii din logica multivalenta. Cele mai importante dintre acestea sunt:
implicatia Kleene - Dienes (sau Dienes - Rescher) se bazeaza pe operatorul cu trei valori logice Rb, definit astfel:
![]()
implicatia Lukasiewicz se bazeaza pe
inlocuirea valorii max(p,q) cu suma
marginita ![]() = min(1, 1-p+q), obtinandu-se relatia numita Ra:
= min(1, 1-p+q), obtinandu-se relatia numita Ra:
![]()
implicatia Zadeh se bazeaza pe
faptul ca in logica bivalenta ![]() are
aceleasi valori de adevar cu
are
aceleasi valori de adevar cu ![]() Aceasta echivalenta se exprima
fuzzy astfel:
Aceasta echivalenta se exprima
fuzzy astfel:
![]()
implicatia
stochastica utilizeaza operatia produs pentru intersectie si
se bazeaza pe egalitatea ![]() :
:
![]()
implicatia Goguen porneste de
la observatia ca in logica multivalenta se impune ca ![]() sa satisfaca relatia
sa satisfaca relatia ![]() Acest lucru se intampla daca
definim
Acest lucru se intampla daca
definim 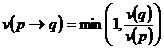 , ceea ce da urmatoarea
relatie:
, ceea ce da urmatoarea
relatie:
 (3.53)
(3.53)
implicatia Godel este una dintre cele mai cunoscute in logica multivalenta:
![]()
Rezulta o relatie frecvent utilizata in logica fuzzy:
![]() (3.55)
(3.55)
implicatia Sharp este mai restrictiva decat Godel:
![]()
![]() (3.57)
(3.57)
implicatia generala este o combinatie intre implicatiile Godel si Sharp, bazata pe formula:
![]()
unde ![]() pot fi s sau g. in termeni fuzzy, aceasta da relatia
pot fi s sau g. in termeni fuzzy, aceasta da relatia ![]() definta astfel:
definta astfel:
![]() (3.59)
(3.59)
implicatia Mamdani este tipica pentru domeniul controlului
fuzzy si se bazeaza pe identitatea ![]() :
:
![]()
Atunci cand nu se mentioneaza altfel, vom considera in continuare in aceasta lucrare mecanismul de inferenta cu implicatie Mamdani.
Intr-o aplicatie de control fuzzy, initial are loc
interpretarea semnificatiei unei reguli pentru o valoare crisp e* a intrarii
procesului. Operatia se numeste focalizare
(firing) si are ca rezultat o valoare fuzzy ![]() a
comenzii (iesirii controlerului), numita taietura si definita astfel:
a
comenzii (iesirii controlerului), numita taietura si definita astfel:
![]() (3.61)
(3.61)
unde 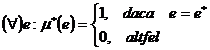
Focalizarea este o inferenta bazata pe regula individuala, numita uneori inferenta scalata sau inferenta maxprodus (fara a avea nimic comun cu compozitia omonima).
Pentru cazul unor reguli multiple (reprezentate simbolic astfel: "daca e este LE(k) atunci u este LU(k)", k = 1,.,n), interpretarea Mamdani a unei reguli este:
![]() (3.62)
(3.62)
In aceasta situatie, semnificatia intregului set de reguli se defineste ca:
![]() (3.63)
(3.63)
sau, cu alte cuvinte:
![]() (3.64)
(3.64)
Daca functia de apartenenta a intrarii crisp
fuzificate e* este ![]() , atunci focalizarea setului de reguli poate
fi exprimata, in acord cu (2.1.61), astfel:
, atunci focalizarea setului de reguli poate
fi exprimata, in acord cu (2.1.61), astfel:
![]() (3.65)
(3.65)
Relatia (3.65) defineste inferenta bazata pe compozitie.
Daca fiecare regula se focalizeaza separat, numim metoda inferenta bazata pe regula individuala. In acest caz se obtin n taieturi de multimi fuzzy, CLU(1),.,CLU(n), adica:
![]() (3.66)
(3.66)
si exista un maximum al tuturor iesirilor:
![]() (3.67)
(3.67)
Se observa ca rezultatul din (3.67) este acelasi cu cel din (3.65).
In concluzie, inferenta bazata pe compozitie
combina mai intai toate regulile in relatia ![]() , care apoi este compusa cu intrarea
fuzzy
, care apoi este compusa cu intrarea
fuzzy![]() , pe cand inferenta bazata pe
regula individuala focalizeaza mai intai fiecare regula cu
intrarea crisp e*, iar apoi combina intr-o singura
multime fuzzy cele n
taieturi obtinute.
, pe cand inferenta bazata pe
regula individuala focalizeaza mai intai fiecare regula cu
intrarea crisp e*, iar apoi combina intr-o singura
multime fuzzy cele n
taieturi obtinute.
|
Politica de confidentialitate |
| Copyright ©
2026 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |