Teorema lui Norton
Conform teoremei lui Norton este posibila simplificarea oricarui circuit liniar, indiferent de complexitate, la un circuit echivalent dotat cu o singura sursa de curent si o rezistenta paralela, ambele conectate la o sarcina. La fel ca in cazul teoremei lui Thevenin, termenul "liniar" are semnificatia teoremei superpozitiei: ecuatiile implicate trebuie sa fie liniare.
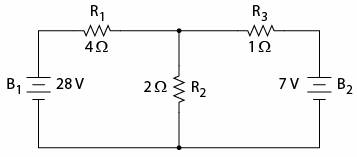
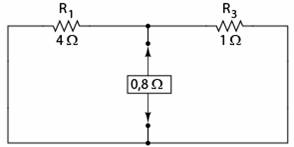
Circuitul initial este cel folosit si in exemplele precedente.
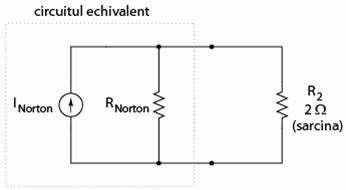
Circuitul echivalent dupa aplicarea teoremei lui Norton va fi cel alaturat.
Sursa de curent este un component a carui scop este furnizarea unei valori constante de curent, indiferent de valoarea tensiunii.
La fel ca in cazul teoremei lui Thevenin, intreg circuitul original, in afara de rezistenta de sarcina, a fost redus la un circuit echivalent ce este mult mai usor de analizat. Pasii folositi pentru calcularea sursei de curent, INorton, si a rezistentei Norton, RNorton, sunt de asemenea similari teoremei precedente.
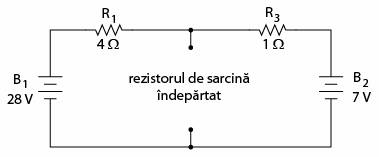
Primul pas este identificarea rezistentei de sarcina si inlaturarea acesteia din circuitul original.
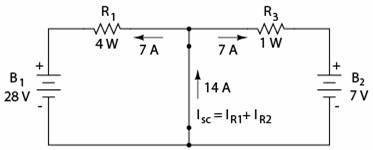
Pentru aflarea curentului Norton, plasam un fir (scurt-circuit) intre cele doua puncte ale sarcinii si determinam curentul rezultat. Observati ca acest pas este exact invers in teorema lui Thevenin, unde am inlocuit sarcina cu un circuit deschis.

Acum ca avem o cadere de 0 V intre punctele de conexiune a sarcinii (inlaturate), inseamna ca valoarea curentului prin R1, in partea stanga a circuitului, depinde doar de tensiunea bateriei B1 si de valoarea rezistorului R1: 7 A (I = E / R). Acelasi lucru este valabil si in partea dreapta a circuitului, unde curentul este tot 7 A. Prin urmare, curentul total prin scurt-circuitul sarcinii este de 14 A si reprezinta curentul sursei Norton (INorton).
Din nou, directia sagetii unei surse de curent este contrara deplasarii reale a electronilor printr-un circuit, notatie ce o folosim in aceasta carte.
Pentru calcularea rezistentei Norton, procedam precum in cazul teoremei lui Thevenin: luam circuitul original, fara rezistenta de sarcina, indepartam sursele de putere conform principiului aplicat in cadrul teoremei superpozitiei (sursele de tensiune le inlocuim cu scurt-circuit iar sursele de tensiune cu circuit deschis) si aflam apoi rezistenta totala dintr-un punct al sarcinii la celalalt (cei doi rezistori legati in paralel).
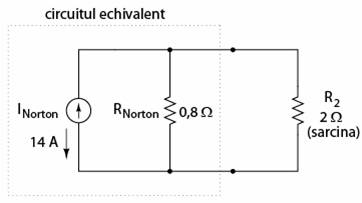
Reconectand rezistenta de sarcina initiala (2 Ω), vom analiza circuitul Norton precum o conexiune paralela simpla. In acest moment circuitul Norton echivalent arata astfel.
|
Marime |
RNorton |
Rsarcina |
Total |
Unitate |
|
E |
8 |
8 |
8 |
V |
|
I |
10 |
4 |
14 |
A |
|
R |
0,8 |
2 |
0,5 |
Ω |
La fel cum am vazut si in cazul teoremei lui Thevenin, singurele informatii utile din aceasta analiza sunt valoarea tensiunii si a curentului prin rezistenta de sarcina R2; celelalte informatii cu privire la circuit sunt irelevante. Avantajul consta in simplitatea analizei circuitului atunci cand avem mai multe valori ale rezistentei de sarcina pentru care vrem sa aflam tensiunea si curentul.
|
Politica de confidentialitate |
| Copyright ©
2025 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |